一种平面约束辅助测量的深空探测器自主天文导航方法

马 辛，宁晓琳，刘 劲，刘 刚

（1.北京航空航天大学前沿科学技术创新研究院，北京100191；2.北京航空航天大学仪器科学与光电工程学院，北京100191；3.武汉科技大学信息科学与工程学院，武汉430081）

引 言

21 世纪初，世界主要航天集团都提出了未来的深空探测计划。我国的火星探测计划也已立项，即将于2020 年开始火星探测。自主天文导航已成为深空探测的关键技术。自主天文导航系统需要在同一时刻观测至少两个导航天体，通过两个天体的位置信息确定探测器的位置和速度[1-5]。导航系统测量误差是制约深空探测自主天文导航精度的重要影响因素，因此，有效抑制测量误差是深空探测器高精度自主导航的主要问题。

在实际深空任务中，深空探测器自主天文导航系统满足一定的内在系统约束。这些约束是实际复杂物理系统内在的固有特性，对这些内在约束建模将提高系统估计性能[8]。系统约束特性的建模与优化已经应用于多个领域，如立体视觉匹配[9]、无源测向定位系统[10-11]等。已有深空探测器自主天文导航方法都尚未考虑导航系统量测量所满足的多种约束条件，更未对约束条件建模优化，导致系统模型中信息相互孤立，未能完全利用所含信息。因此需要对深空探测器自主天文导航系统量测量的平面约束条件进行建模，并针对约束模型，利用约束模型规划算法，辅助优化测量信息，进而可实现深空探测器高精度自主天文导航。

由于平面约束模型为非线性等式和不等式约束模型，因此需要采用非线性规划方法，对模型中的测量信息进行优化。目前已有的非线性规划方法包括：罚函数法（内点、外点、混合）、信赖域反射法、有效集法、序列二次规划（Sequential Quadratic Program‐ming，SQP）方法等。罚函数内点法的基本思想是当迭代点靠近可行域边界时，目标函数值骤然增大，阻止迭代点穿越边界。信赖域法的基本思想是给定一个信赖域半径，以此半径作为位移长度的上界，并以当前迭代点为中心以此上界为半径确定信赖域区域，通过求解这个区域内目标函数二次近似模型的最优点来确定候选位移，若候选位移能使目标函数值有充分的下降量，则接受该候选位移作为新的位移，并保持或扩大信赖域半径，继续新的迭代；否则，需要缩小信赖域半径，再通过求解新的信赖域内的子问题得到新的候选位移，直到满足迭代终止条件。有效集法的基本思想是将非线性优化问题转化为求解一些列的二次规划问题，以目标函数减少为原则，让迭代点循着约束边界前进，直到达到问题的最优点。SQP方法的基本思想是建立原问题的近似二次规划子问题，求解该子问题得到搜索方向，再通过步长规则得到合适的迭代步长，求出下一个迭代点，进入下一次迭代。如何选取优化效果好、计算实时性高的非线性规划方法是急需解决的关键问题[12]。

本文提出一种基于SQP 优化平面约束辅助的深空探测器自主天文导航方法，该方法在对系统非线性不等式几何平面约束建模的基础上，利用SQP 非线性规划方法，对深空探测器自主天文导航系统的非线性不等式约束进行非线性规划，直接辅助减小深空探测器自主导航系统的量测误差；利用Cubature卡尔曼滤波（Cubature Kalman Filter, CKF）-SQP 量测优化非线性约束滤波方法，对深空探测器自主导航系统的状态进行估计，进一步减小系统随机误差，实现深空探测器高精度自主导航。

1 深空探测器平面约束辅助自主天文导航系统

深空探测器平面约束辅助自主天文导航系统可分为敏感器子系统、系统模型子系统和滤波器子系统，如图1 所示。其中，敏感器子系统主要包括用于测量姿态信息的星敏感器、测量火星卫星信息的科学载荷和自主导航敏感器；系统模型子系统主要包括轨道动力学模型、量测模型、量测量和量测量平面约束模型；滤波子系统主要包括平面约束非线性规划、时间更新、量测更新，最终输出探测器的位置和速度。

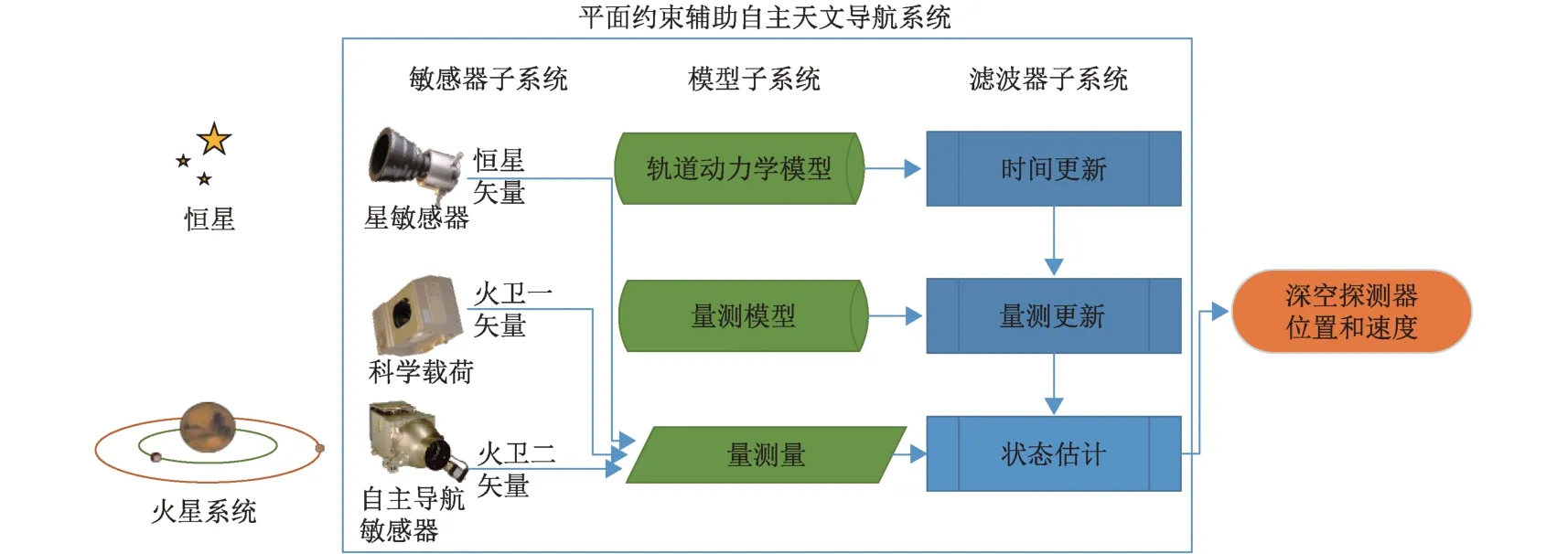
图1 深空探测器平面约束辅助自主天文导航系统框图Fig. 1 The block diagram of deep space probe autonomous celestial navigation system with coplanar constraints

1.1 深空探测器轨道动力学模型

以火星探测为例，在J2000.0 火心赤道惯性坐标系建立火星探测器的轨道动力学模型[1-3]

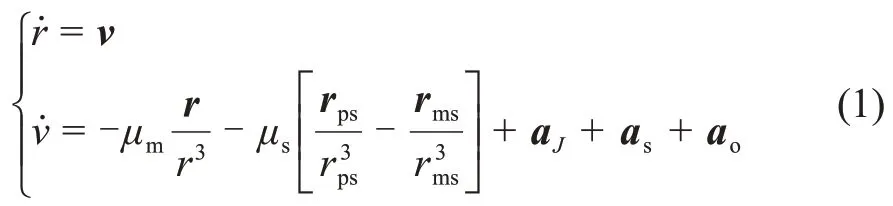
其中：r=[x,y,z]T为探测器在火心惯性坐标系中的位置矢量；v=[vx,vy,vz]T为探测器在火心惯性坐标系中的速度矢量；μm为火星引力常数；μs为太阳引力常数；rps为日心到探测器的位置矢量；rms为日心到火心的位置矢量；aJ为火星非球形引力摄动加速度，as为太阳辐射压力加速度，ao为其他未建模摄动加速度。

可简写为

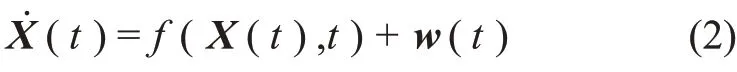
其中：X=[x,y,z,vx,vy,vz]T为天文测角导航系统的状态矢量，f(⋅)为天文测角导航系统的非线性连续状态转移函数，w=[w1,w2,w3,w4,w5,w6]T为天文测角导航系统的状态模型误差。

1.2 深空探测器量测模型

以火卫一和火卫二的天体矢量方向作为天文测角导航系统的量测量，可由敏感器获得的像元像线坐标计算得到，则火卫一、火卫二天体矢量方向的量测模型可以表示为

其中：Lphobos和Ldeimos分别为火卫一和火卫二天体矢量方向，rphobos和rdeimos分别为火卫一和火卫二在火心惯性坐标系中的位置矢量，为探测器与火卫一和火卫二之间的距离。

令Z=[LphobosT,LdeimosT]T， 量 测 噪 声V=[vlphobosT,vldeimosT]T，vl1,vl2分别为Lphobos,Ldeimos的观测误差，则分别以火卫一和火卫二的天体矢量方向作为观测量的量测模型可表示为

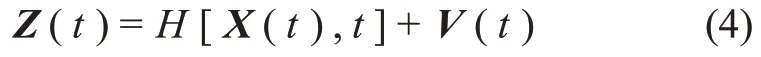
其中，H(⋅)为天文测角自主导航系统以火卫一和火卫二的天体矢量方向为观测量的量测方程。

1.3 量测量几何平面约束模型

在同一时刻，两个导航天体到探测器的矢量方向L0=[m0,n0,p0]T和L1=[m1,n1,p1]T不 共 线 (如 图 2 所示)，即

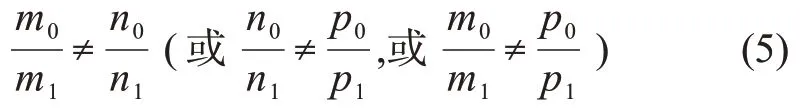
式中：m0,n0,p0,m1,n1,p1为第1 个和第2 个导航天体到探测器的矢量方向。

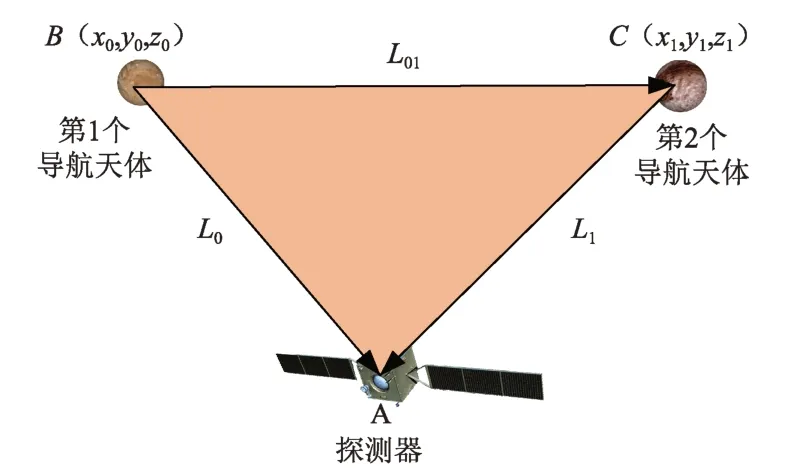
图2 天文测角几何平面约束示意图Fig.2 Geometric coplanar constraints in celestial navigation

由于L0和L1在同一平面内，L01和L0在同一平面内，且L01和L1也在同一平面内，因此可以确定三个矢量方向在同一平面内，如图2所示，因此可得

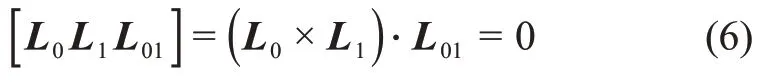
对于实际天文测角自主导航系统，测量所得的导航天体到探测器的矢量方向与真实的导航天体到探测器的矢量方向存在误差，则根据导航天体到探测器真实的矢量方向与其测量误差的关系，测量所得的第i个导航天体到探测器的矢量方向可定义为

根据测量所得的导航天体到探测器的矢量方向的定义如式(7)所示，可得

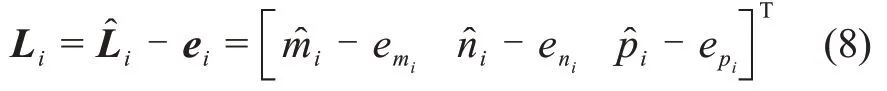
则式(6)可以表示为

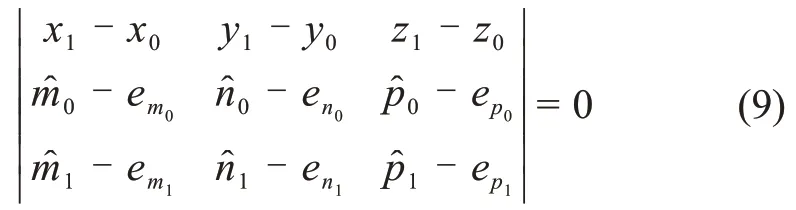
由于式(6)表示真实的2个导航天体与探测器之间各矢量的关系，因此无论探测器与2个导航天体之间的矢量方向测量误差有多大，都不会影响式(6)所表示的平面约束关系。

天文测角导航测量误差的平面约束，可以采用基于约束最优问题的最优化方法对测量误差进行进一步限制，从而减小测量误差对导航精度的影响。本论文采用天文测角视线单位矢量方向误差平方和作为目标函数，以视线单位矢量方向共面作为约束条件，建立最优化模型

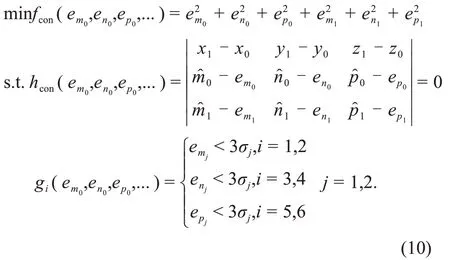
其中：em0,en0,ep0,em1,en1,ep1为量测量天体视线矢量方向m0,n0,p0,m1,n1,p1的测量误差，σj为第j个导航天体的测量误差标准差。从式(10)可以看出，基于几何平面约束的测量误差最优化问题是一个非线性规划问题，其约束条件包含一个等式约束和一个不等式约束。

2 基于SQP优化的约束Cubature卡尔曼滤波

基于SQP优化的约束Cubature卡尔曼滤波的具体流程如图3 所示，首先对计算Cubature 采样点和权值，根据系统状态模型计算各采样点的一步预测值，再通过权值加权完成时间更新；其次利用SQP 非线性规划算法，优化测量误差和量测量；最后根据系统量测模型和SQP 优化后的量测值，进行量测更新，最后得到系统的状态估计和状态误差方差，输出探测器的位置和速度。本节给出SQP 非线性规划算法基本步骤[12]。

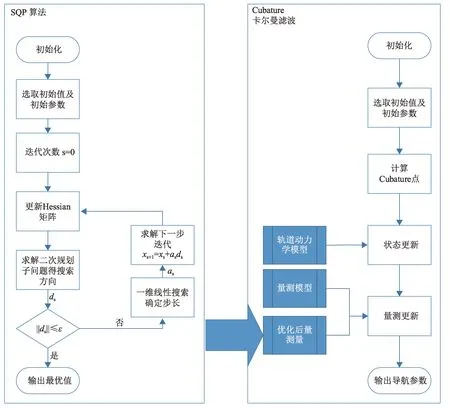
图3 基于SQP优化的约束Cubature卡尔曼滤波Fig. 3 Constraint Cubature Kalman Filter based on SQP

将量测量所满足的平面约束（如式（10）所示）展开为拉格朗日二次逼近函数

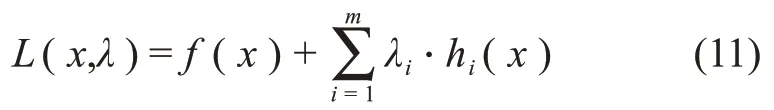
其中，λi为第i个约束的拉格朗日乘子。

线性化非线性约束，可得二次规划子问题，其目标函数为

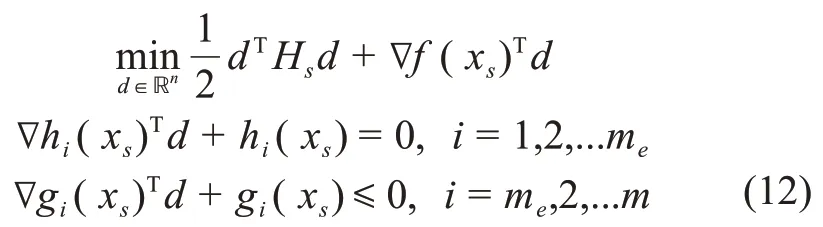
其中：d为全变量搜索方向；Hs为拉格朗日函数Hes‐sian 矩阵的正定拟牛顿近似，其可以采用BFGS 方法更新，即

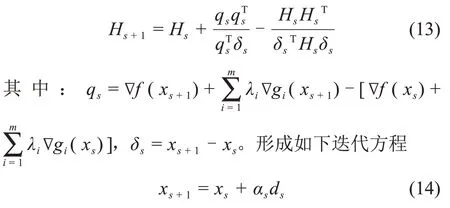
其中：ds为xs到xs+1的向量，步长参数αs通过合适的线性搜索方式确定，使指标函数值得到足够的精度。

3 计算机仿真

3.1 仿真条件

本节采用2018 年火星探测任务为仿真对象，探测器轨道由Satellite Tool Kit Astrogator 产生，此次任务在J2000日心平黄道坐标系中，探测器发射时间为2018-05-20，预计抵达火星时间为2019-01-14，轨道历元时间2018-05-23，08:23:24.009 UTCG，初始轨道参数为[−70 597 583.471 308 km, −134 137 866.280 822 km, 23 192.415 638 km, 28.251 309 km/s, −15.795 096 km/s,0.055 146 km/s]T，仿真时间为2019-01-12，18: 04: 36.650 UTCG 到 2019-01-14， 10: 25: 29.737 UTCG，接近火星时间为，2019-01-14，10:25:29.737 UCTG，近火点高度600 km，远火点高度8万km，轨道积分方法和步长RKF89/1 s，初始位置和速度的误差为[1 000 km,1 000 km,1 000 km,1 m/s,1 m/s,1 m/s]T，火卫一矢量方向测量误差6″，火卫二矢量方向测量误差3″，非线性规划方法最大迭代次数为400次，最优化阈值1×10-6，步长阈值1×10-6。

3.2 仿真结果

1）不同非线性约束规划算法优化结果

图4给出了在相同初始条件下不同非线性约束规划算法对量测量的优化结果。由图可以看出，信赖域反射法、内点法、有限集法、序列二次规划法都可有效减小精度较低的量测量测量误差（火卫一矢量方向测量误差），但对精度较高的测量误差抑制效果不明显。表1给出了不同非线性约束规划算法对量测量的详细优化结果。从表1可以看出，不同非线性约束规划算法对精度较低的量测量测量误差进行了明显的优化，优化后火卫一和火卫二测量信息可优化至接近的精度，但精度较高的测量误差与优化前相比精度略有下降。这是由于平面约束方法的特性是将2个带有误差的矢量约束至同一平面内，因此约束过程中，精度较差的矢量会对精度较高的矢量造成一定的影响。从表1还可以看出，信赖域反射法和内点法量测优化后的结果相同，优化指标函数值也相同，具有相同的优化精度；有限集法可以得到最高的火卫二矢量方向量测优化精度，但其对火卫一矢量方向量测优化精度与其他方法相比最低；序列二次规划法相比其他3种方法可以获得最小的优化指标函数值，优化效果最好，优化后火卫一的测量误差为3.461 1″，火卫二的测量误差为3.409 8″。此外，表1还给出了4种非线性规划方法计算时间的比较，序列二次规划方法用时最少。

图4 不同非线性约束规划算法对量测量的优化结果Fig. 4 Measurement optimization results for different nonlinear constrained programming algorithms

表1 不同非线性约束规划算法对量测量的优化结果对比表Table 1 Comparisons of measurement optimization result using different nonlinear constrained programming algorithms

2）导航天体不同测量误差的优化结果

图5 给出了当深空探测器火卫一和火卫二测量误差分别为2 ″和1 ″时的测量优化结果。由图可以看出，采用序列二次规划法可有效减小精度较低的量测量测量误差（火卫一矢量方向测量误差）。表2 给出了导航天体不同测量误差的详细优化结果。从表2 可以看出，当深空探测器火卫一和火卫二测量误差分别为2 ″和1 ″时，优化后火卫一测量误差为1.098 5″，火卫二测量误差为1.096 4″；当深空探测器火卫一和火卫二测量误差均为1 ″时，优化后火卫一的测量误差为0.696 4″，火卫二的测量误差为0.698 1″；当深空探测器火卫一和火卫二测量误差均为3 ″时，优化后火卫一测量误差为2.095 8″，火卫二测量误差为2.104 8″。当2 个导航天体测量误差精度相同时，优化后火卫一和火卫二测量信息精度可提高接近30%。当2 个导航天体测量误差精度不同时，优化后火卫一和火卫二测量信息可优化至接近的精度，精度较差的导航天体的优化结果更为明显。这是由于本文所提方法采用了平面约束，将测量所得火卫一矢量和火卫二矢量约束至同一平面，因此精度较高的测量矢量精度决定了2 个矢量的测量精度。

3）平面约束辅助测量后的导航结果

图6 和表3 给出了平面约束辅助量测优化深空探测器自主天文导航结果，与无平面约束辅助优化的深空探测器自主天文导航结果进行了比较。由图6和表3可以看出，滤波收敛后无平面约束辅助量测优化的自主天文导航方法的平均位置误差为11.305 6 km（RMS），最大位置误差为21.947 9 km，平均速度误差为0.269 8 m/s（RMS），最大速度误差为0.609 5 m/s；基于平面约束辅助量测的自主天文导航方法平均位置误差为7.665 2 km（RMS），最大位置误差为18.426 2 km，平均速度误差为0.208 7 m/s（RMS），最大速度误差0.575 5 m/s。由此可以看出，平面约束可以减小矢量测量方向的随机测量误差，提高自主天文导航精度。

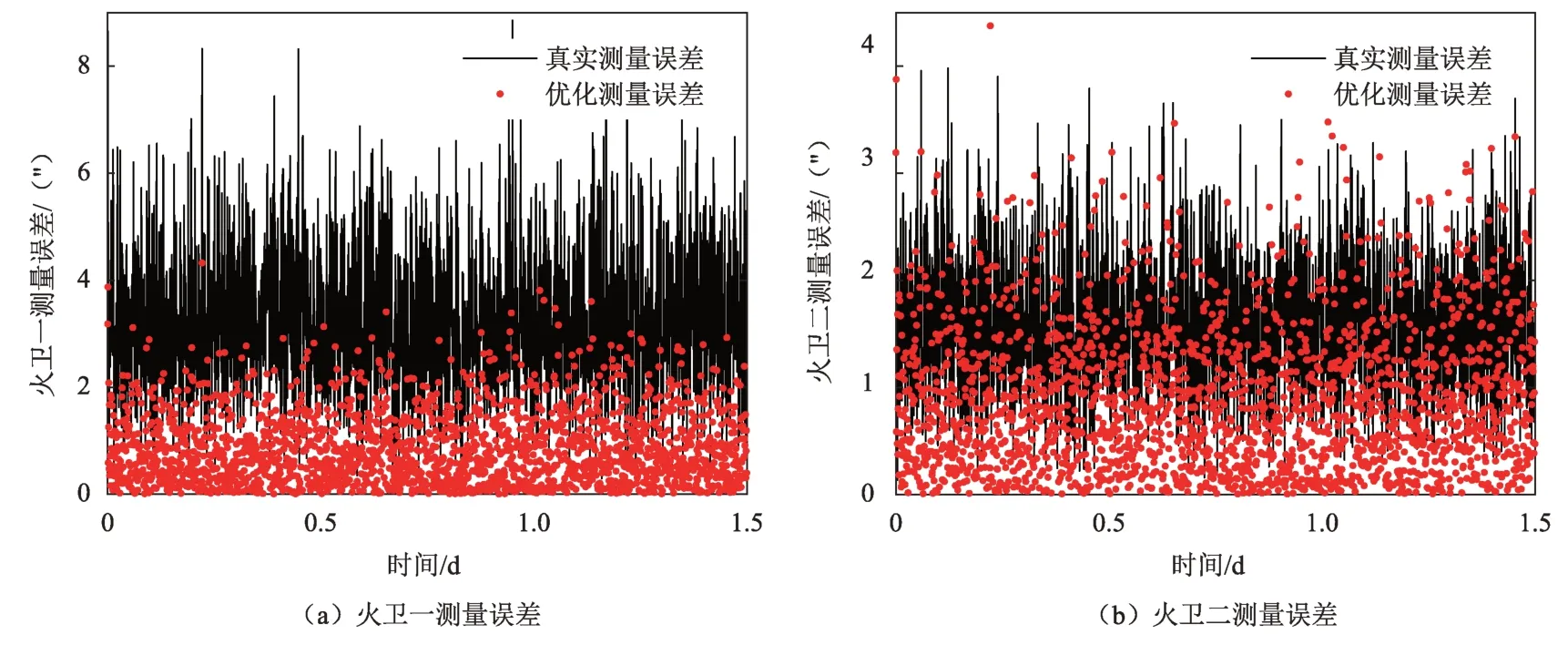
图5 导航天体不同测量误差的优化结果Fig. 5 Measurement optimization results of different measurement accuracies

表2 导航天体不同测量误差的优化结果对比表Table 2 Comparisons of measurement optimization results of different measurement accuracies

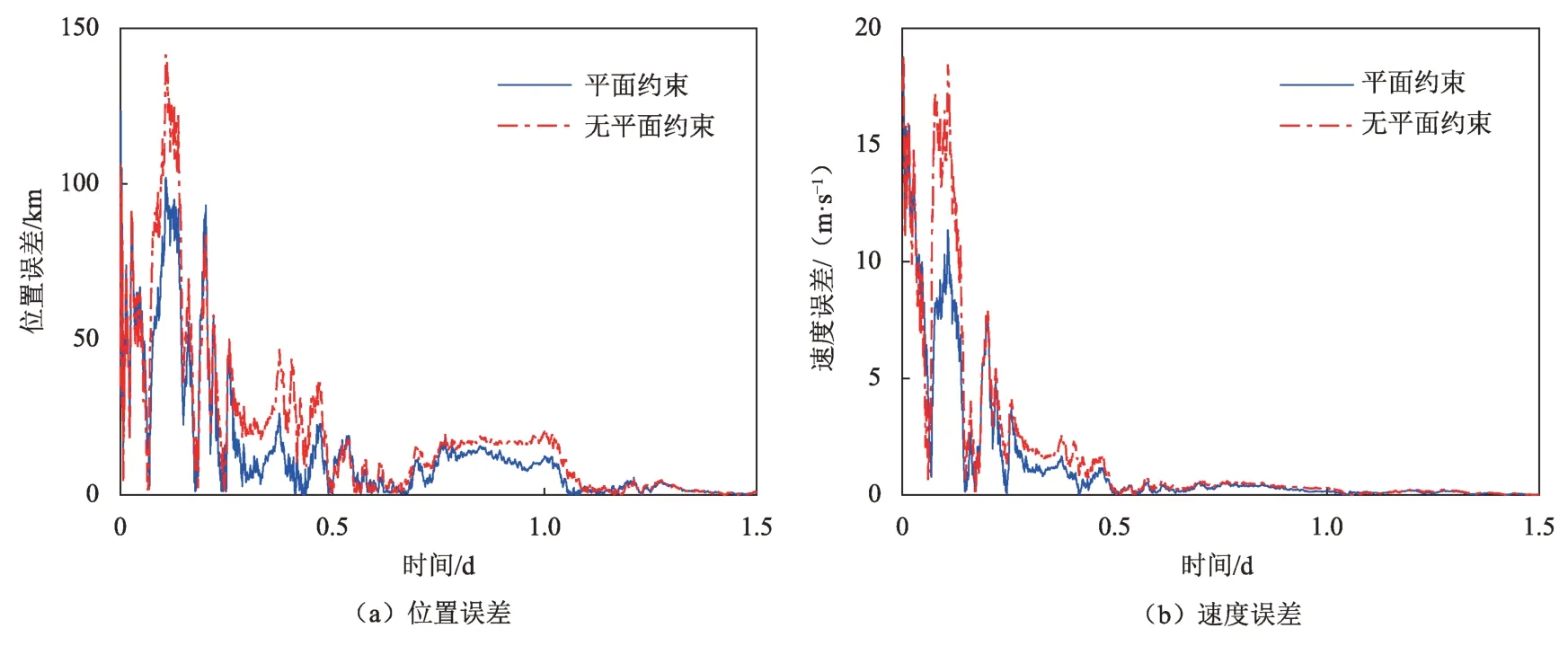
图6 平面约束辅助量测优化深空探测器自主天文导航结果Fig. 6 Autonomous celestial navigation results with coplanar constraints aided measurement

表3 平面约束辅助量测优化的深空探测器自主天文导航结果对比Table 3 Comparisons of autonomous celestial navigation results with coplanar constraints aided measurement

4 结 论

本文针对抑制深空探测器自主天文导航系统测量误差这一问题，提出了一种平面约束辅助测量的深空探测器自主天文导航方法，该方法在对系统非线性不等式几何平面约束建模的基础上，利用了SQP 非线性规划方法，对深空探测器自主天文导航系统的非线性不等式约束进行了非线性规划，直接辅助减小了深空探测器自主导航系统的量测误差；利用CKF-SQP量测优化非线性约束滤波方法，对深空探测器自主导航系统的状态进行估计，进一步减小了系统随机误差，提高了深空探测自主天文导航的精度。仿真结果表明，所提方法可以有效抑制了测量误差，尤其对精度较低的测量误差抑制效果显著，实现了深空探测器高精度自主导航。