高精度模型下Halo轨道设计研究

曹鹏飞，李维国，王俊彦，李海阳

（1.北京航天飞行控制中心，北京100094；2.中国卫星发射测控系统部，北京100120；3.国防科学技术大学空天科学学院，长沙410073）

引 言

早在20 世纪Apollo 时代，美国的Farquhar 提出了利用地月L2 点（以下简称LL2）附近的Halo 轨道实现月球背面与地球持续通信[1]。近年来，随着平动点任务的不断提出与实施，摄动模型下的Halo 轨道设计问题一直是研究热点。Farquhar 等[2]较早研究了如何控制航天器使其运行在Halo轨道的近似轨道上。Gomez等[3]基于Floquet理论和不变流形理论，给出了一种摄动模型下的轨道设计方法。Howell 等[4-5]基于标称轨迹提出了Halo 轨道靶点法控制策略，该方法具有适用范围广、简单可靠等优点，但由于其控制精度和代价函数中的权重矩阵与保持间隔密切相关，有一定局限性。Qi等[6]在Howell研究基础上，进一步提出了Halo 轨道正切靶点法轨道设计方法。Mehrdad等[7]考虑了太阳引力摄动与月球轨道偏心率摄动，采用线性二次调节器（Linear Quadratic Regulator，LQR）和多重打靶策略（Multiple Shooting，MS）设计了地月平动点Halo 轨道，但过程较为复杂，且燃料成本偏高。徐明等[8]基于Halo 轨道偏差动力学方程，提出了Halo 轨道线性周期保持控制策略。彭海军等[9]基于圆型限制性三体问题（Circular Restricted Three Body Problem，CR3BP），采用SDRE（State Dependent Riccati Equation，SDRE）方法设计了用于平动点轨道维持控制的非线性次优跟踪控制器。车征等[10]在CR3BP 的基础上引入了太阳引力摄动，研究了LL2 点Halo 轨道设计问题。刘磊等[11]基于CR3BP下的平动点轨道运动特性和微分修正策略提出了连续环绕控制方法，该方法中平动点轨道初值取自CR3BP一阶近似结果。

本文在文献[11]研究思路基础上，提高了初值精度，进一步提出了高精度多层序列二次规划（Se‐quence Quadratic Program，SQP）修正的求解方法。首先，推导了CR3BP 质心会合坐标系与地心J2000坐标系之间的转换关系，并在此基础上，将CR3BP下的闭合Halo 轨道转换到地心J2000 坐标系得到了高精度模型下Halo 轨道迭代初值。其次，采用SQP构造多层迭代格式，在高精度模型下对初值进行逐层修正。通过仿真测试，文章所述方法的可行性与有效性得到了验证。

1 动力学模型

本文采用两种动力学模型，即CR3BP 模型和高精度模型，模拟地月空间飞行器的运动规律。

1.1 圆型限制性三体问题

CR3BP，即假设大天体和小天体绕其公共质心做匀速圆周运动，研究第三体在两主天体共同引力下的运动问题。在CR3BP 中，常用的坐标系为质心会合坐标系B-xyz，对于地月系统，其原点位于地月公共质心B，x轴由地球指向月球，z轴指向地月系统角动量方向，y轴与其他两轴构成右手坐标系。

为简化动力学方程，通常引入归一化单位，地月系统长度单位为地月质心平均距离DU=384 400 km，质量单位MU 为地球质量M1和月球质量M2之和，时间单位可有上述两参数导出。引入质量比μ，即

航天器在B-xyz坐标系下的无量纲动力学方程为

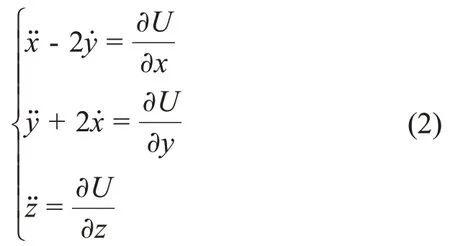
其中：U为与位置相关的伪势能函数，即

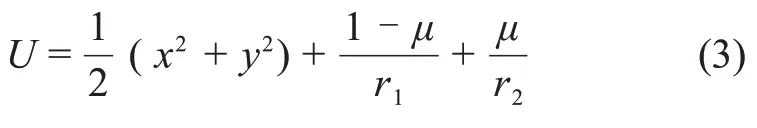
式中

1.2 高精度模型

高精度模型考虑了地球中心引力、日月引力摄动、地月非球形引力摄动、太阳光压摄动以及金星、木星等三体摄动等。在地心J2000坐标系下，忽略地球潮汐和相对论效应等微小摄动量的影响。

航天器的动力学方程为

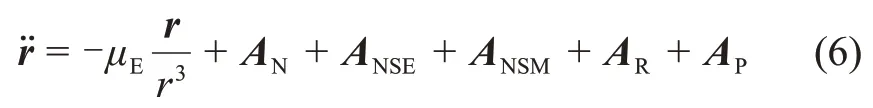
其中：r为地心位置矢量；μE为地球引力常数；AN为N体引力摄动加速度，星体间空间几何关系通过DE405/LE405星历求解；ANSE为地球非球形摄动，取WGS84引力场模型8×8阶计算；ANSM为月球非球形摄动，取LP165P引力场模型8×8阶计算；AR为太阳光压摄动；AP为推进加速度。

1.3 Halo轨道

Halo 轨道是共线平动点附近的三维周期轨道，在平动点任务中被广泛应用。CR3BP会合坐标系下，Halo 轨道关于xz面对称，与xz面交于两点，通常取其中距离x轴较远的点与x轴的距离作为表征Halo轨道大小的参数，称之为法向幅值Az。CR3BP 下，Halo轨道的计算通常先采用Richardson三阶近似解析解[12]获取初值，然后再利用微分修正法对初值进行修正，详细推到过程可参考文献[13]。

2 高精度模型下Halo轨道设计

2.1 初值计算

CR3BP 下的闭合Halo 轨道可为高精度模型下Halo 轨道设计提供良好初值，但由于动力学模型的差异，二者的转换过程并不直观。

本节以地月系统为例，详细推导了CR3BP 质心会合坐标系B-xyz与地心J2000 坐标系OE-XJYJZJ之间的转换关系。如图1所示，给出了两坐标系的几何构型图。假设航天器在OE-XJYJZJ中的位置矢量为R=[xJ,yJ,zJ]T， 单 位 为 km， 速 度 矢 量 为V=，单位为km/s；在B-xyz中的位置矢量为r=[x,y,z]T，速度矢量为v=，单位采用归一化单位。引入自定义坐标系——高精度质心会合坐标系B-XYZ，其原点位于地月质心，坐标轴指向与坐标系B-xyz相同，区别在于该坐标系中的地月和平动点的位置并非固定，而是实时变化。

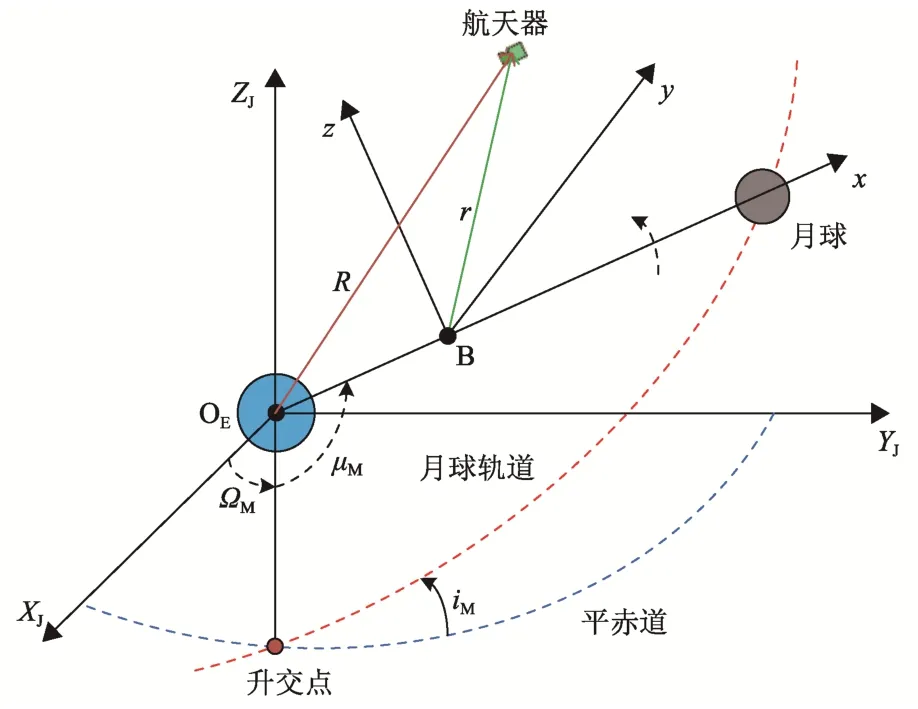
图1 坐标系几何构型图Fig. 1 The geometries of the coordinate frames

首先，推导位置矢量转换关系。假设历元时刻为t0，月球轨道半长轴为aM，偏心率为eM，升交点赤经为ΩM，白赤交角为iM，近地点幅角为ωM，真近点角为fM。由二体问题可知，地月距离为

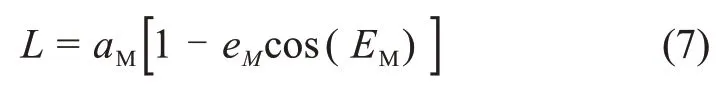
其中：EM为偏近点角。

记归一化后的L为，即

由坐标系定义可知，在B-XYZ中，地球位置矢量为rB1=， 航 天 器 位 置 矢 量 为rB2=。因此，航天器相对于地球的位置矢量为

下一步，将rB3转换到地心J2000坐标系，该转换由ΩM、iM和uM三个欧拉角决定。计算公式为

其中：uM为纬度幅角。

由图1 可知，B-XYZ到地心J2000 坐标系的转换矩阵为

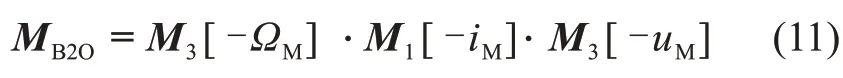
矩阵M1[λ]与M3[λ]满足的条件为

在完成坐标旋转后，将归一化单位转换为国际单位制即可完成位置矢量的转换，具体公式如下

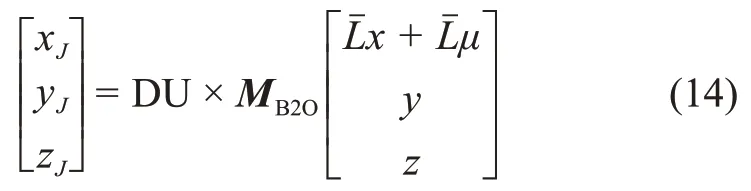
速度转换思路与位置转换类似，区别在于前者需要考虑牵连加速度项。在高精度模型下，地月距离实时变化，其径向变化速率为

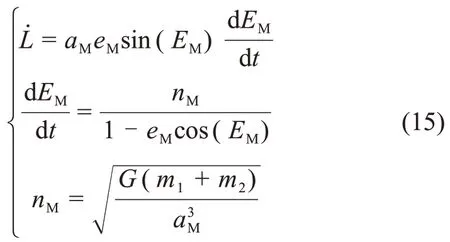
其中：nM为月球公转平均角速度。

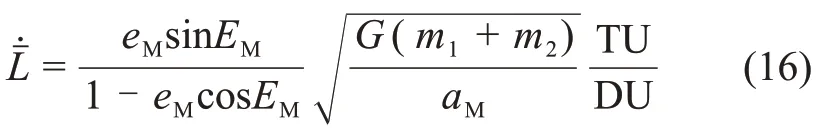
由式（9）可知，在B-XYZ中航天器相对地心的速度矢量为

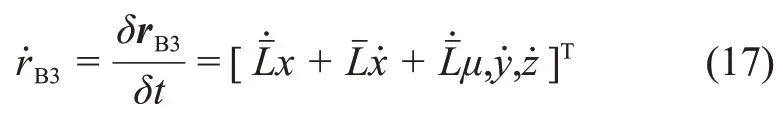
引入地心白道惯性系OE-XIYIZI，其原点位于地心，坐标轴指向与某一瞬时的B-XYZ相同。B-XYZ相对于地心的角速度矢量在OE-XIYIZI中可以表示为ωΜ=[0,0,ω]Τ，其中ω为瞬时旋转速率。记归一化后的ω为ωnorm，表达式为

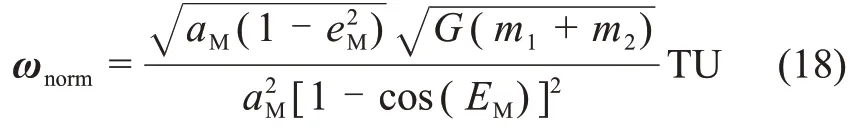
进一步可得，B-XYZ相对于OE-XIYIZI的牵连速度，归一化后的表达式为

综合式（17）和（19），在完成坐标和单位转换后即可完成速度矢量的转换，具体公式如下

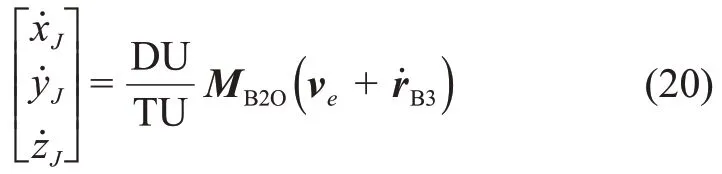
2.2 多层序列二次规划修正

由于复杂摄动力的影响，高精度模型下的Halo轨道将不再闭合。为了便于分析，本节将参照CR3BP 下的Halo 轨道特性，给出高精度模型下Halo轨道圈数的定义。如图2 所示，在坐标系B-XYZ中，Halo 轨道由xz面出发，第2 次到达xz面时轨道为1/2圈，第3 次到达xz面为1 圈，第4 次到达xz面时为2圈，依次类推。

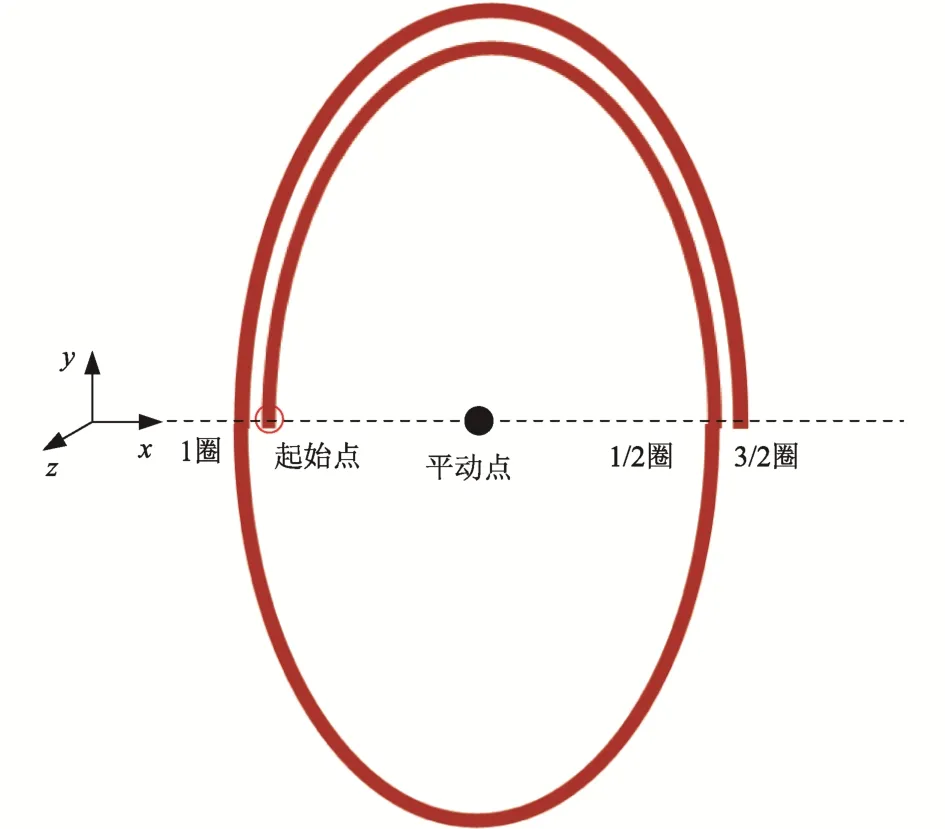
图2 高精度模型下Halo轨道的圈数定义Fig. 2 The definition of the number of Halo orbits in the high precision model

在B-xyz坐标系下，Halo轨道关于xz面对称，即在xz面处x或z方向的速度分量为零。基于Halo轨道该特性，本节将采用SQP 构造多层迭代格式，给出高精度模型Halo轨道设计方法，具体流程为：

第1步：参考文献[13]，计算CR3BP质心会合坐标系下Halo轨道在xz处的积分状态量x0；

第2 步：采用2.1 小节方法，将x0转换到地心J2000坐标系，转换结果记为X0，将其作为高精度模型下Halo轨道修正初值；

第3步：在高精度模型下采用SQP对X0的3个速度分量进行多层修正，具体流程如图3所示。

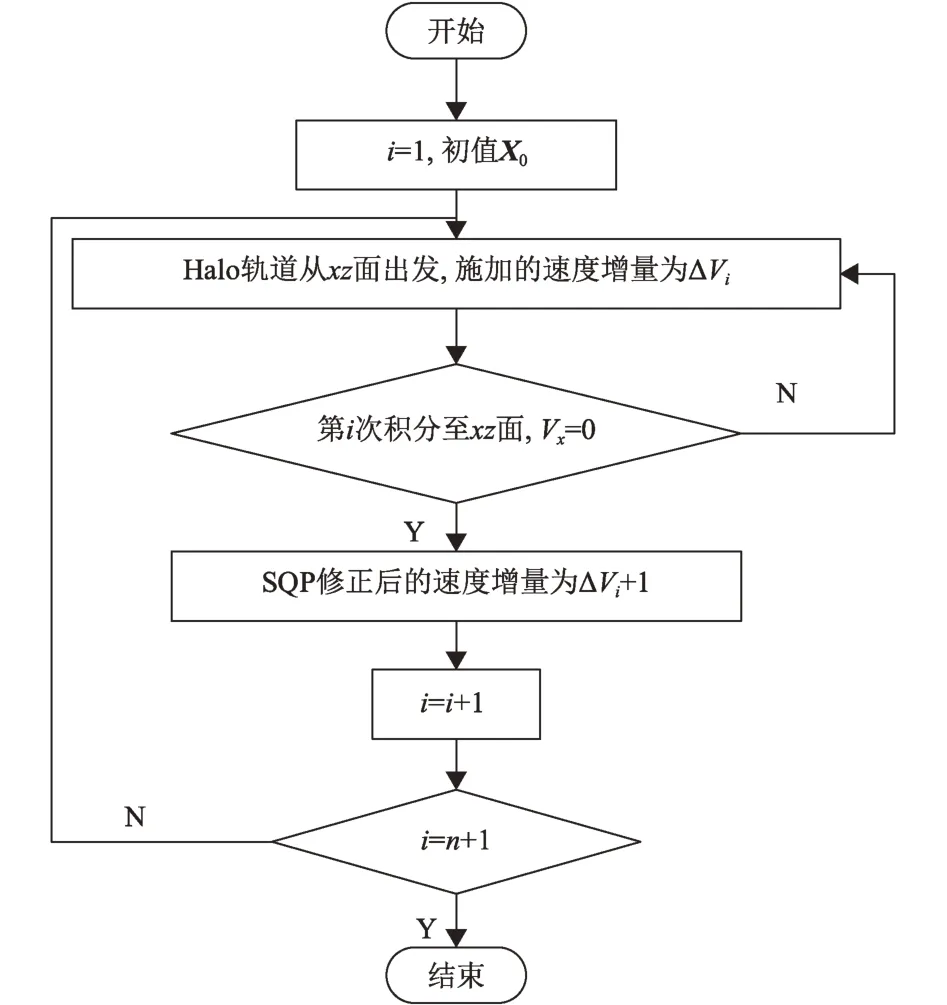
图3 初值修正流程图Fig. 3 The flow chart of initial value correction

第1层：优化变量为施加的速度增量ΔV1，即

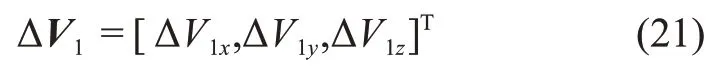
约束条件为轨道第1 次到达xz面时Vx= 0，优化结果记为ΔV2。高精度模型下，轨道在xz面处x或z方向的速度分量接近于零但不严格为零，因此ΔV1并非最优解，需要进一步修正。

第2 层：优化变量为ΔV2，约束条件为轨道第2次到达xz面时Vx= 0，优化结果记为ΔV3。依次类推，当修正层数n=4时，修正脉冲的量级已非常小。当n> 4 时，由于修正脉冲的量级接近摄动力量级，程序将终止。因此对于地月系统，修正层数n不宜大于4次，该结论与文献[11]结果相吻合。

高精度模型下为了得到飞行多圈的光滑Halo 轨道，需要定期对轨道进行维持控制，单次维持所消耗的速度增量的求解流程与图3 类似，这里不再赘述。且由前面的分析可知，速度增量的施加位置为xz面处，维持间隔应不宜大于2圈。

3 算例验证

给出高精度模型下Halo 轨道设计实例，参考文献[7]给出参数配置：Halo轨道法向幅值Az为30 000 km，周期为14.25 天，方向为南向，位于LL2 点附近；历元时刻为2025 年1 月1 日00:00:0.000UTCG；跳秒与STK11 一致，取37 s；选用RKF7（8）变步长积分器，相对误差和绝对误差设为10-13。

首先，通过采用文献[13]提供的方法，计算CR3BP质心会合坐标系下Halo轨道，并利用式（13）和式（20）将其初始点参数转换到地心J2000 坐标系。其次，采用2.2 节所述方法对初始点速度分量进行修正，为加快计算收敛速度，这里只修正Y方向的速度分量，修正层数n设为4。地心J2000坐标系下修正前后的初始点参数见表1。

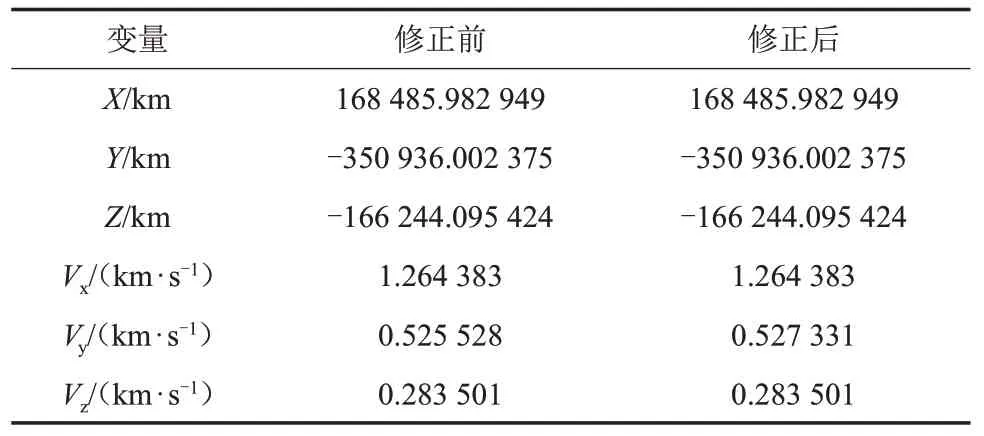
表1 Halo轨道初始点参数Table 1 The initial point parameters of Halo orbit

直接将修正前的初始点参数代入高精度模型积分一个周期，并将轨道数据实时转换到高精度LL2点会合坐标系，得到的轨道如图4所示。将修正后的初始点参数代入高精度模型，积分1圈，即终止条件为轨道第2次到达xz面时Vx= 0，并将轨道数据实时转换到高精度LL2 点会合坐标系，得到的轨道如图5所示。

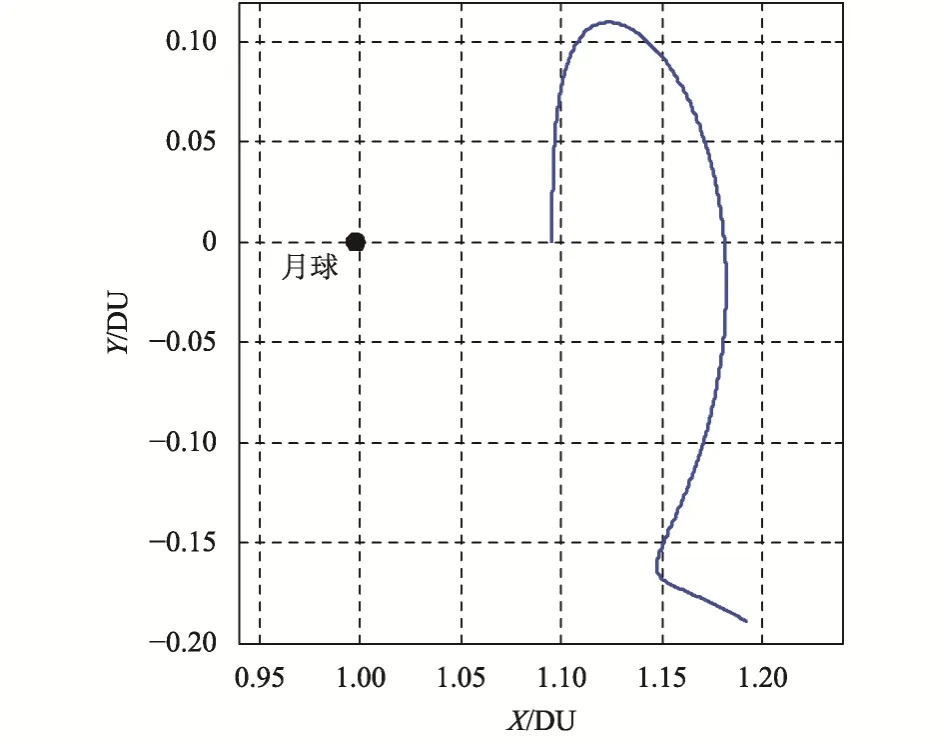
图4 修正前初始点参数递推得到的轨迹Fig. 4 The trajectory derived from the unrevised initial point parameters

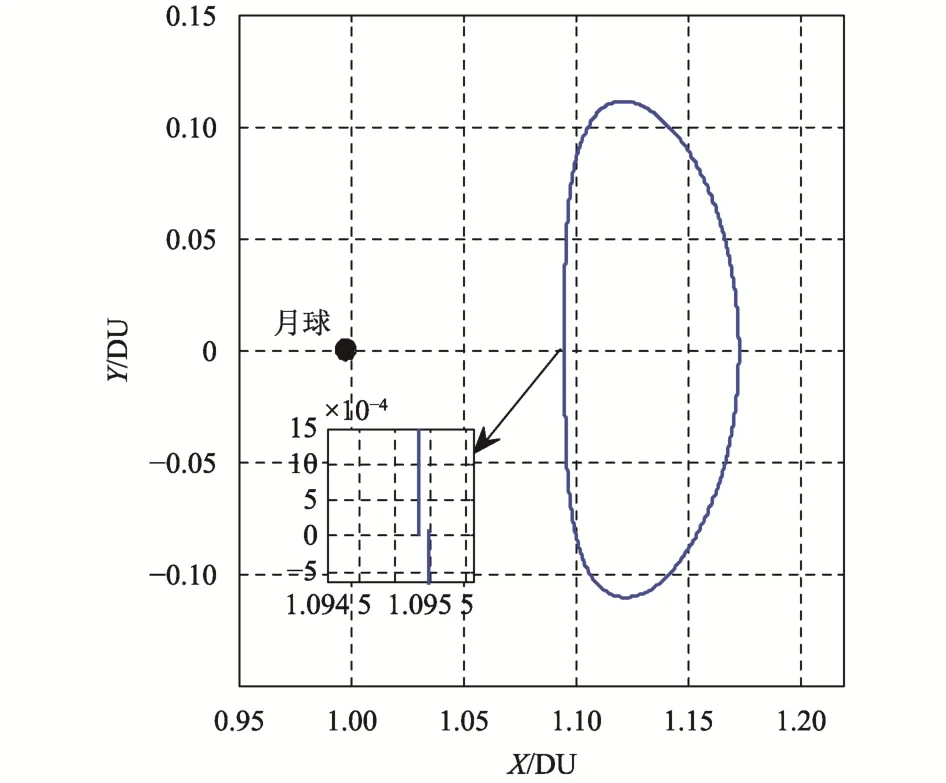
图5 修正后初始点参数递推得到的轨迹Fig. 5 The trajectory derived from the revised initial point parameters

对比图4和图5可知，CR3BP下的闭合Halo轨道在高精度模型下飞行约半个周期后将急剧发散，而修正后轨道在高精度模型下周期性保持较好，但仍未闭合。因此，对于长期飞行于Halo 轨道的航天器，需要定期进行轨道维持控制。

仍以上述算例为基础，给出高精度模型下Halo轨道维持实例。采用图3的计算流程，SQP修正层数n设为4，维持间隔设为1圈，对图5中的轨道进行为期1年的维持，得到的飞行轨迹在高精度LL2点会合坐标系下的投影如图6所示，维持总次数和消耗的总速度增量见表2。

表2 维持间隔与维持总速度增量的关系Table 2 The relationship between the maintenance interval and the maintenance impulsive consumption

图6 高精度地LL2点会合坐标系下飞行一年的Halo轨道轨迹Fig. 6 The flying trajectories of the Halo orbit for one year in the high precision LL2 point synodic coordinate system

此外，表2还给出了不同维持间隔方案时的维持总次数和总的速度增量消耗信息。由表2可知：①当维持间隔为0.5圈、1圈和1.5圈时，所消耗的总速度增量差异并不大；②当维持间隔由1.5 圈增加为2 圈时，所消耗的速度增量急剧增加，这是由于维持间隔过大造成累积偏差较大，从而导致速度增量消耗增多；③对于LL2 点Halo 轨道，综合考虑速度增量消耗与维持频率，最佳维持间隔应为1.5 圈。对比文献[7]的计算结果，发现多层SQP 修正方法在高精度Halo 轨道维持方面具有维持间隔长和燃料成本低等优点。

4 结 论

本文研究了高精度模型下共线平动点附近Halo轨道的设计问题。推导了CR3BP 质心会合坐标系与高精度模型地心J2000坐标系之间的转换关系，并在此基础上，将CR3BP 下的闭合Halo 轨道转换到地心J2000 坐标系得到了高精度模型下Halo 轨道迭代初值。通过采用SQP 对初值进行多层修正，得到了在高精度模型下的Halo 轨道。进一步研究发现，该方法还可用于摄动模型下Halo轨道的维持设计。最后，仿真算例验证了方法的可行性与正确性，研究结果可为未来平动点任务的标称轨道设计提供参考。