基于交会模式的月球大椭圆轨道编队飞行控制

李革非，盛庆轩，刘 勇

（1.北京航天飞行控制中心，北京100094；2.航天飞行动力学重点实验室，北京100094）

引 言

月球轨道超长波天文观测微卫星是“嫦娥4 号”任务的搭载试验项目之一，利用CZ-4C运载火箭剩余发射能力，发射两颗微卫星，在月球轨道进行深空编队飞行关键技术演示验证，开展超长波天文干涉测量等探索性研究[1]。绕月超长波天文观测微卫星计划，将首次实现绕月编队飞行。两颗微卫星搭载“嫦娥4号”中继星进入地月转移轨道，完成地月转移、近月制动。进入环月大椭圆轨道后，在地面测控支持下，经过远距离接近、中距离调整，完成编队构型捕获，形成相对距离在1～10 km 范围内可变的环月轨道编队，具备开展科学探测条件[2]。

关于椭圆轨道航天器编队运动及其轨道设计，国内研究大多集中于主航天器为圆轨道，从航天器运行于小偏心率轨道的编队任务[3-5]。至于研究方法，国外部分研究者采用动力学法，包括Hill 方程和Lawden 方程[6-7]，但前者适于短期编队，后者形式复杂不适于编队设计。也有众多学者采纳和应用了运动学法，探讨了圆轨道和大椭圆轨道编队飞行相对运动[3,5,8-9]。文献[10]应用运动学法研究了大偏心率远距离航天器编队飞行设计。文献[11～12]则采用C-W方程解析解进行了编队阵形设计，然而只能应用于小偏心率近距离范围内的编队设计。

航天器交会轨道控制使得相距较远的两个航天器在指定时间到达同一地点或指定地点，可作为从远距离接近到近距离编队的一种控制方法。近地轨道交会对接技术日臻成熟，我国已圆满完成了“神舟8 号”到“神舟11 号”以及“天舟1 号”等共5 次交会对接。文献[13]介绍了我国首次空间交会对接远距离导引方案设计与飞行验证。文献[14～16]对空间交会对接机动和路径进行了比较全面的数学建模。文献[17]建立了规划变量对远距离导引终点六自由度的独立控制方程，设计了标称整体规划与动态逐级规划相结合的多模式规划策略。文献[18～19]对交会远距离导引段误差敏感度进行了研究。国内对于月球轨道交会也有初步研究，文献[20]提出了月球轨道交会远程导引段的4 脉冲变轨策略方案，文献[21]进行了环月快速交会调相策略设计与任务分析，文献[22]利用“嫦娥5 号”飞行试验器拓展试验，对3 脉冲目标器调相策略和4脉冲交会策略进行了在轨验证。但关于月球轨道交会基本局限于环月近圆轨道。

由于微卫星运行于300 km × 9 100 km 的环月大椭圆轨道，受摄运动与圆轨道相比差异较大。因此，近地轨道交会控制模型和算法在环月轨道、尤其是在环月大椭圆轨道的适应性研究是非常有必要的。

针对月球大椭圆轨道编队飞行控制，本文采用相对轨道根数描述，基于多脉冲交会控制模式，设计了以交会终点满足编队飞行状态的轨道控制策略，基于对月球大椭圆轨道控制特性的分析，通过对轨道平面、拱线、形状和相位等轨道全要素的控制，按照远距离接近、中距离调整和编队形成的分段控制思路，通过多次渐进式轨道机动，形成满足科学试验要求的编队飞行。

1 微卫星轨道飞行过程

微卫星经历发射、地月转移、近月制动、编队形成、绕月工作共5个阶段。微卫星A与B间隔30 s先后与运载火箭分离进入地月转移轨道，各自独立控制飞向月球。在地月转移轨道飞行约112 h 到达月球。卫星到达近月点的目标参数为月球轨道倾角20°，近月点高度300 km。卫星到达近月点附近实施制动捕获，经过4 次捕获机动后，进入近月点高度300 km、远月点高度9 100 km的目标轨道。之后，两颗卫星开始远距离接近至形成编队的飞行控制。形成编队后的环月工作阶段，涵盖长期运行过程中的构形维持和基线控制等。

依据科学任务对编队构形的需求，结合大椭圆轨道相对运动特性，设计串行编队为编队理想构形。编队目标为：双星同轨面大椭圆轨道编队飞行，相对距离在1～10 km变化。结合大椭圆轨道相对运动特性，图1 所示为环月大椭圆轨道编队相对运动的理想构形。

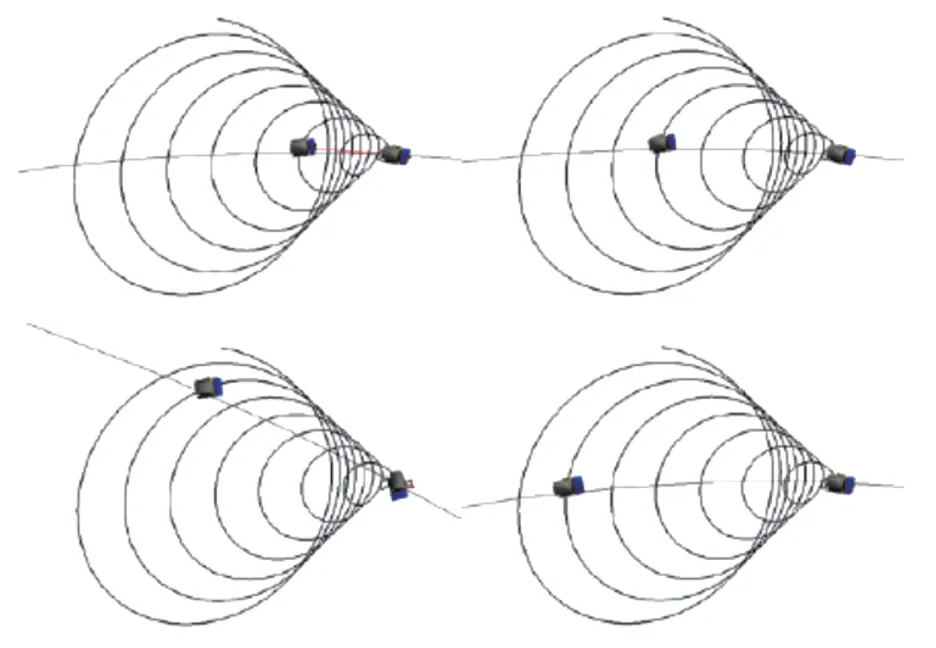
图1 编队理想构形相对运动轨迹Fig.1 Relative motion of ideal configuration

受大椭圆轨道偏心率较大的影响，无控状态下，B星在轨道平面内相对A星做周期性往复运动：远月点附近时，两星最近；近月点附近时，两星最远。

绕月飞行后，两颗卫星运行于近月点300 km、远月点9 100 km的大椭圆轨道。由于导航和控制系统偏差的存在，A/B两颗卫星的轨道存在一定偏差，相对距离在1 000 km以上，因此，需要实施轨道控制任务，在地面测控资源保障下，通过多次渐进式轨道机动，使得两星逐渐接近至相对距离10 km 范围之内，并通过编队构形保持控制，使得基线在1～10 km 之间动态变化。

2 编队轨道控制策略

2.1 控制目标

采用轨道参数描述串行编队目标如下：

1）串行编队两卫星目标轨道参数差：Δa= 0，Δe=0，Δi=0，ΔΩ=0，Δω=0，Δu。

2）入轨和近月捕获时，B星相位始终滞后A星，编队实现B星相对A星跟飞串行。

2.2 控制模型

两颗微卫星各自奔月飞行和近月制动；环月后，轨道参数可能具有较大的偏差。在编队形成及维持阶段，两颗卫星为形成编队而协调工作，以一颗卫星为基准星，另一颗卫星实施轨道控制实现编队飞行。根据跟飞编队控制目标，需对卫星6 个轨道要素进行控制。文献[23]给出轨道要素的修正控制公式。

1）轨道平面修正

在两轨道平面交点利用法向速度增量进行轨道倾角i、升交点赤经Ω的修正控制。设Δvn1,Δvn2分别表示在两个轨道平面交点的法向速度增量。

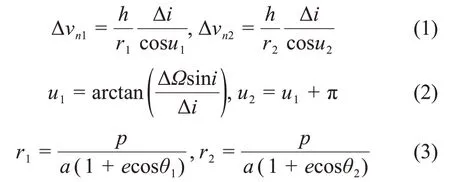
其中，h=μa(1 -e2)。

上式表明，Δvn的大小与卫星月心距离有关。对于椭圆轨道，需考虑不同轨控位置u1/u2的r1/r2大小对控制量的影响，尽量选择在r值较大的位置进行轨控，使得速度增量较小。表1 给出了在近月点300 km 远月点9 100 km 轨道不同位置对升交点和倾角修正的不同控制量。

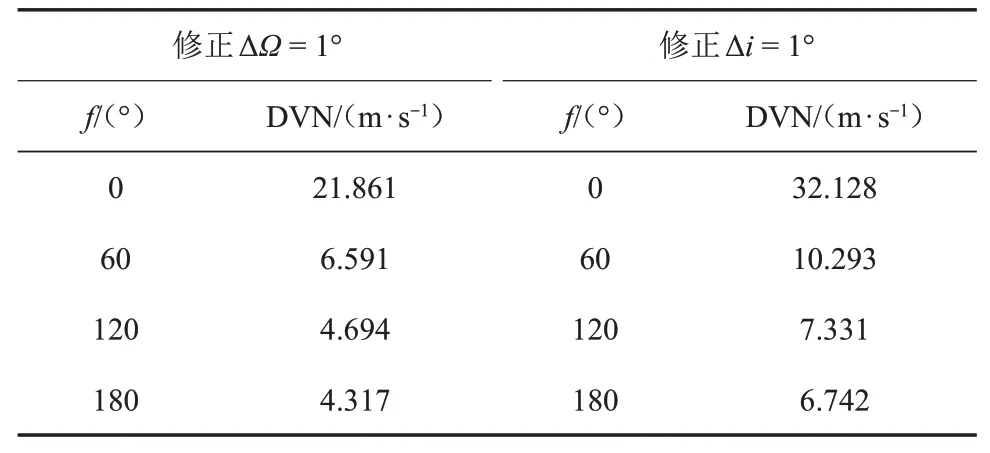
表1 不同位置修正ΔΩ=1°或Δi=1°的速度增量Table 1 ∆V to correct ∆Ω =1°or ∆i=1°at different argument

另外，轨道平面修正控制会引起轨道平面内参数发生变化。如，DVN=22.680 m/s，将引起轨道参数变化Δhp=-24.8 km，Δha=-28.3 km，Δω=0.6°。

2）近月点幅角修正

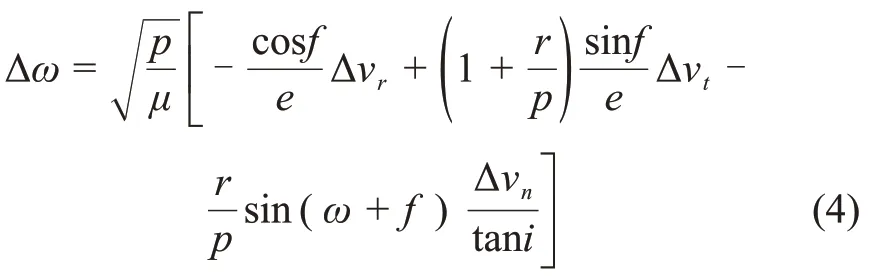
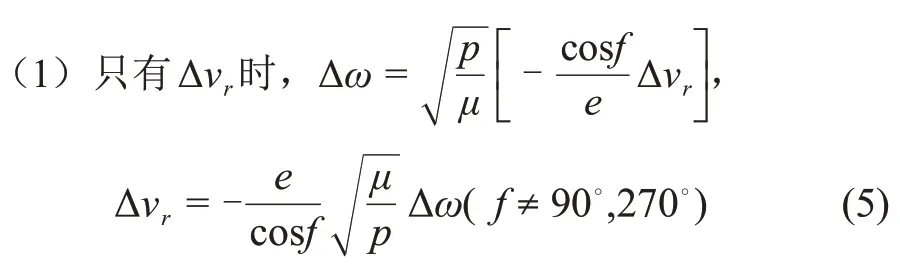
当f= 0°,180°，Δvr=，修正 Δω控制量最小。

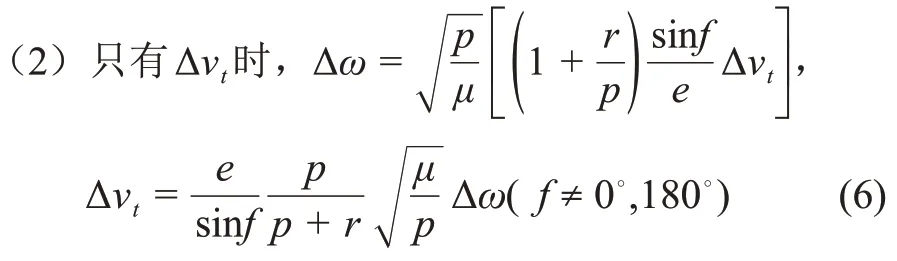
当f= 90°,270°， Δvt=Δω， 修 正Δω控制量最小。

对于相同数值的Δvr，Δvt，Δvt比Δvr控Δω的效率高，但对a，e的影响较大。表2给出了修正Δω=1°所需的Δvr，Δvt的速度增量。

表2 不同控制方向修正Δω=1°的速度增量Table 2 ∆V to correct ∆ω=1°with different direction

3）双脉冲控制半长轴、偏心率和近月点幅角

针对双脉冲控制a，e，ω，本文基于圆锥曲线公式设计了下列求解算法。

已知初始轨道：p0,e0,θ0，目标轨道目标：Δω,pt,et。设第一脉冲点位置为u1，待求参数为第二脉冲点位置u2和双水平脉冲控制量Δv1,Δv2。根据输入和输出，各要素关系如图2所示。

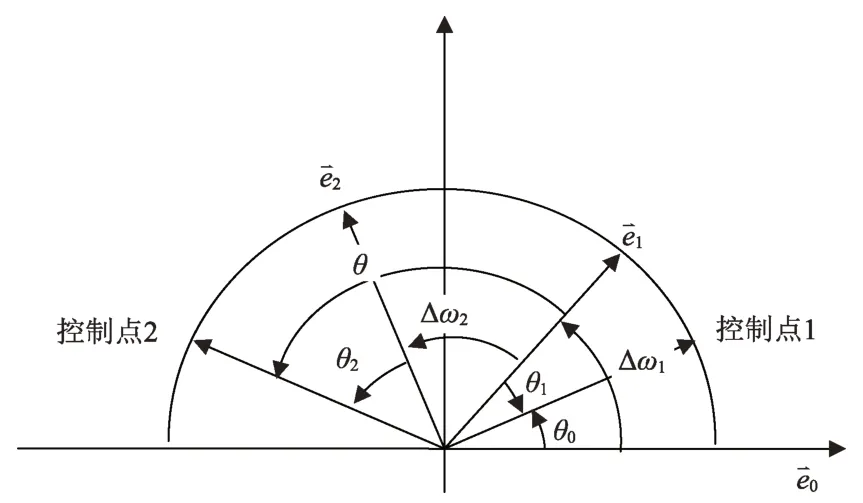
图2 双脉冲求解示意图Fig.2 Sketch of double impulses solved

根据输入条件，可知2个脉冲控制点的控前、控后的径向速度相同，2个脉冲控制点的控前、控后的径向距离相同，根据圆锥曲线公式，可得

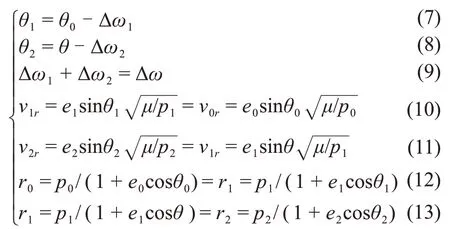
此外，还有Δu=θ2+ Δω-θ0和Δu=θ-θ1。其中，p1,e1,θ1,θ,θ2,Δω1,Δω2都未知。方程个数与未知参数个数相同。

在给定θ1的情况下，由式（10）和式（12）可解得p1,e1；由式（7）得Δω1，由式(9)得Δω2，由式（8）和式（11）得θ,θ2。最后，上述公式变为通过求解θ1使得式（13）成立，即求解r2=f(θ1)的函数。通过迭代求解可得θ2,r1,r2。已知θ1,θ2,r1,r2，即可求解水平脉冲Δv1,Δv2。

4）平面内轨道调相

轨道调相通过调整轨道半长轴实现

椭圆轨道不同轨道位置的调相控制量不同，即相同速度增量在不同控制位置对轨道半长轴的影响不同，如近月点处1 m/s速度增量，半长轴变化约34 km；远月点处1 m/s 速度增量，半长轴变化约6 km，因此，采用近月点调相控制更节省控制量。

2.3 控制策略

超长波天文观测试验的最佳位置是在月球背面的近月点附近，符合“月球背面能够有效屏蔽来自地球的射电信号干扰，拥有太阳系中近乎最安静的电磁环境，是开展超长波观测的最佳选择”的结论[2]。选择近月点作为双星编队轨道控制的目标瞄准点。

双星编队轨道控制策略设计思路为：基于多脉冲交会控制模式，设计以交会终点满足编队飞行状态的轨道控制策略，对平面、拱线、形状和相位等轨道全要素实施控制。以A星或B星为基准，在指定近月点使得双星轨道根数a、e、i、Ω、ω保持一致，M有微小不同，从而达到串行编队的相对距离目标。本文设计了5脉冲定点交会策略实现编队目标（见表3）。

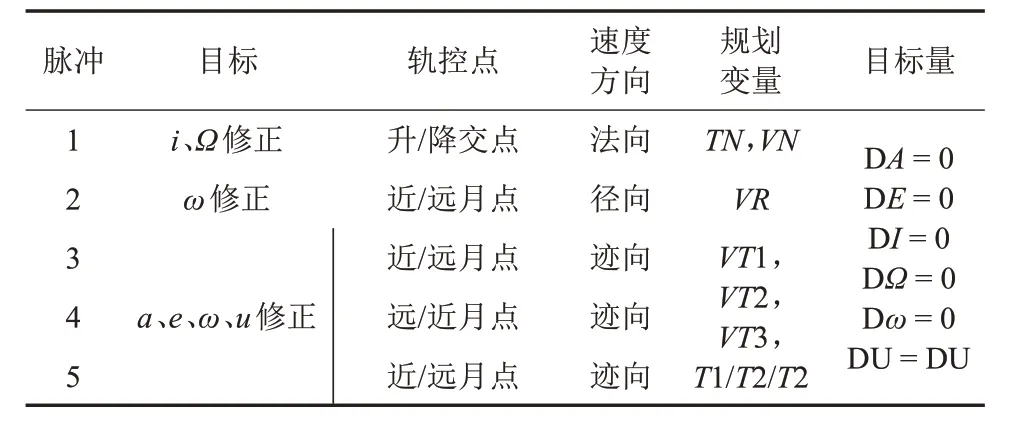
表3 5脉冲编队轨道控制策略Table 3 Orbit maneuver strategy of 5 impulses for formation

设计思路如下。

1）当轨道平面i和Ω的偏差较大时，法向控制量对轨道偏心率和近月点幅角产生较大影响，因此，将轨道平面修正控制设计为第一脉冲。规划变量包括作为轨控时刻的两卫星轨道平面交点时刻TN和法向控制速度增量VN。

2）当近月点幅角ω偏差较大时，近月点幅角的修正对轨道平面内的参数影响较大，如半长轴和相位，因此，将近月点幅角修正控制设计为第二脉冲。由于沿迹向脉冲相比径向脉冲对于半长轴影响甚大，因此，选择径向脉冲修正近月点幅角。规划变量为径向控制速度增量VR。

3）之后采用3 个沿迹向脉冲进行平面内4 参数a，e，ω，u的联合控制，实现轨道平面内指定时间的交会相位。规划变量为3 个迹向控制速度增量VT1，VT2，VT3以及其中之一的控制时刻T1/T2/T2。

在远距离接近、中距离调整编队控制时，由于两卫星之间轨道平面和轨道拱线相差较大，采用5脉冲策略；在近距离编队捕获时，两卫星轨道平面和轨道拱线基本一致，不再需要修正，则采用迹向3脉冲控制策略，只实现轨道平面内交会控制。

2.4 迭代算法

为精确控制微卫星实现编队飞行控制目标，需对多脉冲编队策略的控制参数进行准确计算，得到高精度的轨道控制时刻和控制量。

按照轨道控制模型解析公式计算各次脉冲控制初值，采用多脉冲线性制导方法，将需规划的多脉冲控制时刻和控制量作为求解变量，进行迭代求解。

文献[22]给出了线性制导方法。航天器轨道的终端状态为初始状态的函数，初始状态P为当前时刻航天器轨道参数，终端状态Q为终端时刻航天器目标轨道参数，函数形式为：Q=f(P)。

线性制导方法的基本思想为航天器实际轨道与标称轨道的偏差为小量，将实际轨道在标称轨道附近泰勒展开，保留线性项，得到如下线性控制方程

其中：ΔQ为终端时刻航天器目标状态QT与实际状态Q的偏差，即ΔQ=Q-QT；ΔP为控制向量；K为状态变量对控制参数的敏感矩阵，称雅可比矩阵。

若初始参数P0对应终端参数Q0与要求的目标终端参数QT存在一定偏差，则利用该式，通过迭代可计算出修正终端参数偏差Q0-QT所需的初始参数修正量ΔP，即：ΔP=K-1⋅ΔQ。如果控制变量个数与目标参数个数不相等，则可利用最小范数广义逆计算控制变量ΔP，即：ΔP=KT(K⋅KT)-1⋅ΔQ。

多脉冲控制的修正量为多组速度增量和控制点时刻，目标参数为交会点两卫星相对轨道参数，Δa=0，Δe=0，Δi=0，ΔΩ=0，Δω=0，Δu。

3 编队轨道控制仿真

3.1 控制分段

超长波天文观测试验的最佳位置是在月球背面的近月点附近，因此，编队轨道目标为在近月点实现双星相对距离小于1～10 km，即以A 星为基准，在指定近月点双星轨道根数a、e、i、Ω、ω保持一致，M有微小不同。根据微卫星近月点高度300 km、远月点高度9 100 km的大椭圆轨道，近月点纬度幅角差与相对距离的关系如下：

DU = 0.1°，DS = 3.630 km；DU = 2°，DS =72.609 km；DU=14°，DS=510.656 km。

考虑到导航误差、控制误差等影响，采用渐进式的编队控制方式，将编队飞行控制分为远距离接近段、中距离调整段和编队捕获段。远距离段控制目标为：瞄准指定近月点双星轨道根数前5个参数保持一致，相位相差14°，即近月点相对距离在500 km 左右；中距离段控制目标为：相位相差2°，即近月点相对距离在100 km 以内；编队捕获段控制目标为：相位相差0.1°，即近月点相对距离在5 km 以内。实际飞行中，考虑两颗卫星燃料均衡使用，可轮流两颗卫星实施轨道机动控制。本文重点对编队轨道控制策略进行分析，对于均衡两星燃料、轮流轨道控制不在此详述。

3.2 策略计算

1）轨道根数

卫星轨道动力学模型考虑月球引力场32×32 阶次，地球和太阳质点引力，太阳光压力（见表4）。

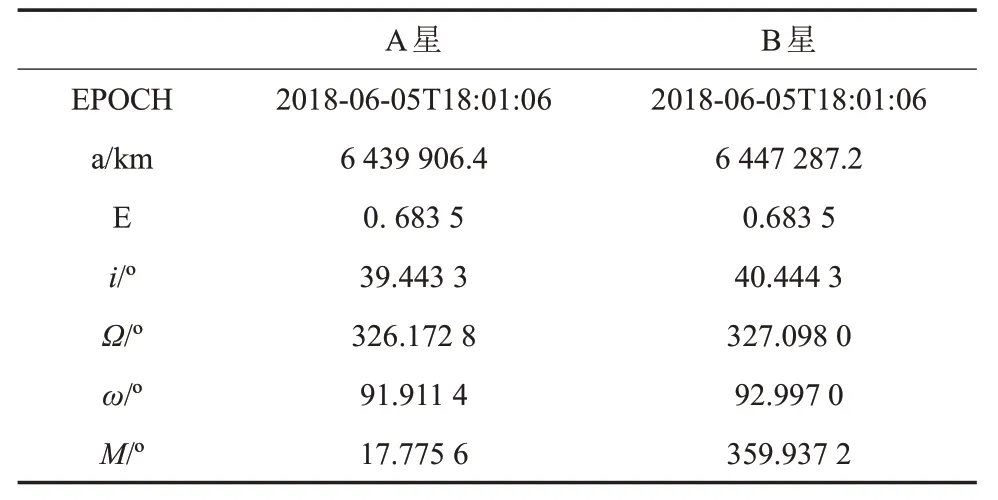
表4 微卫星A和B初始环月大椭圆轨道根数Table 4 Orbit elements of two microsatellites

2）轨控策略

考虑地面测控的测定轨和上行注入安排，2次轨控间隔2圈，按照远距离、中距离和近距离3段接续式编队控制策略设计（见表5）。

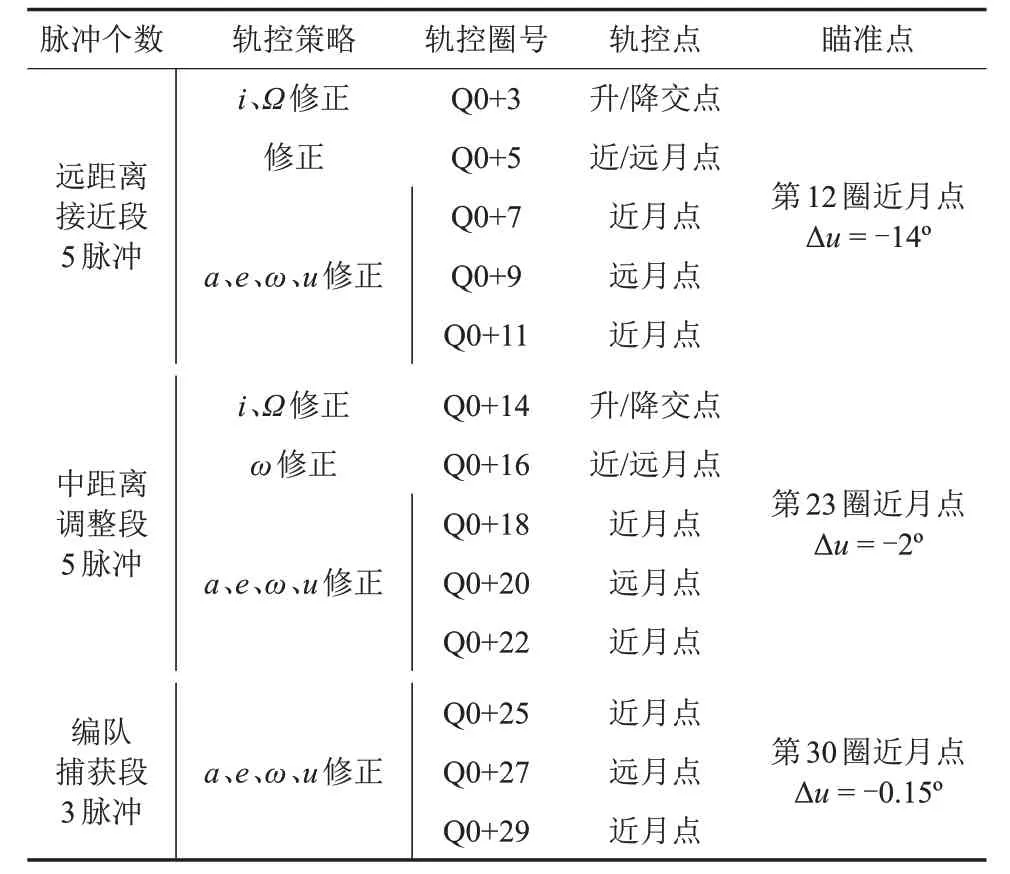
表5 编队轨道控制策略Table 5 Orbit maneuver strategy of formation

3）远距离接近段策略的优化分析

按照轨道平面修正分别在升轨交点和降轨交点、近月点幅角修正分别在真近点角f=0°和f=180°、轨道平面内交会脉冲在近月点和远月点，设计了4种远距离接近策略（见表6）。

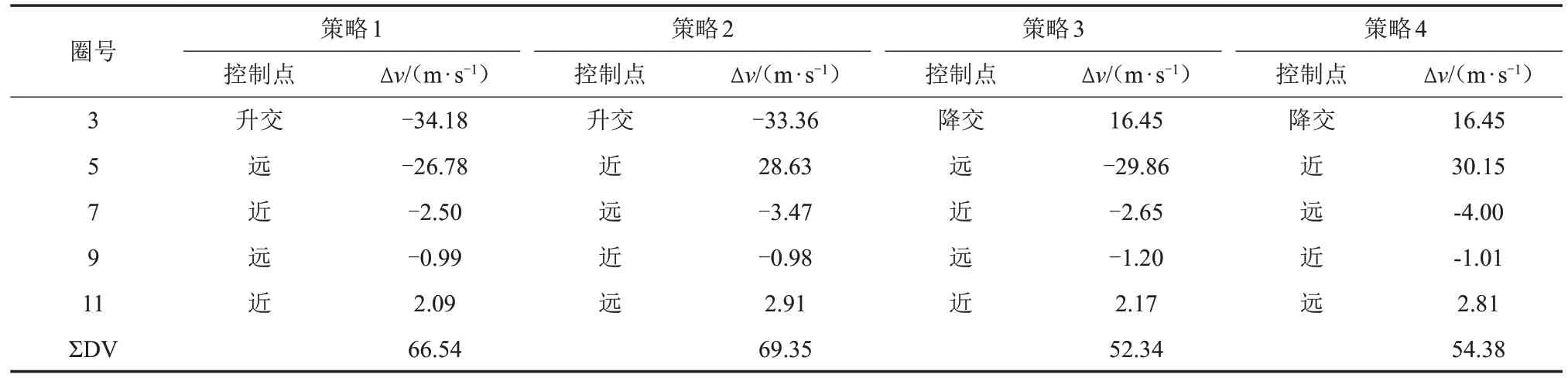
表6 远距离接近段的多组编队控制策略比较Table 6 Comparison of maneuver strategies of far distance

表6结果表明：

①第1 脉冲是修正i、Ω的法向脉冲，策略3 和4的第一脉冲小于策略1 和2，这是由于降轨交点处月心距离大于升轨交点处月心距离。

②第2脉冲是修正ω的径向脉冲，在近、远月点控制量均为最小，由于法向脉冲对轨道拱线有影响，策略1和2的结果接近，策略3和4接近。

③第3、4、5脉冲为平面内4参数a，e，ω，u的联合控制脉冲，由于近月点调相控制效率高，近-远-近的策略优于远-近-远的策略。

因此，以策略3结果的总速度增量最小，这与模型分析结论是一致的。

④远距离接近段+中距离调整段+编队捕获段的接续仿真。以上述远距离策略3，接续中距离和近距离控制策略（见表7），实现最终的编队飞行。图3给出了3 段轨道控制及B 星相对A 星的X-Z相对运动轨迹。图3表明，月球大椭圆轨道条件下，受双星初始轨道根数各参数差异较大的影响，相对运动轨迹呈现椭圆扭曲形态，在远距离接近段5 脉冲策略控制下，消除了轨道平面差异、拱线差异和偏心率差异，使得在后续中距离调整段和近距离捕获段时，双星轨道根数的差异主要为半长轴和相位的较小差异，相对运动轨迹逐渐向规则椭圆的形态变化。

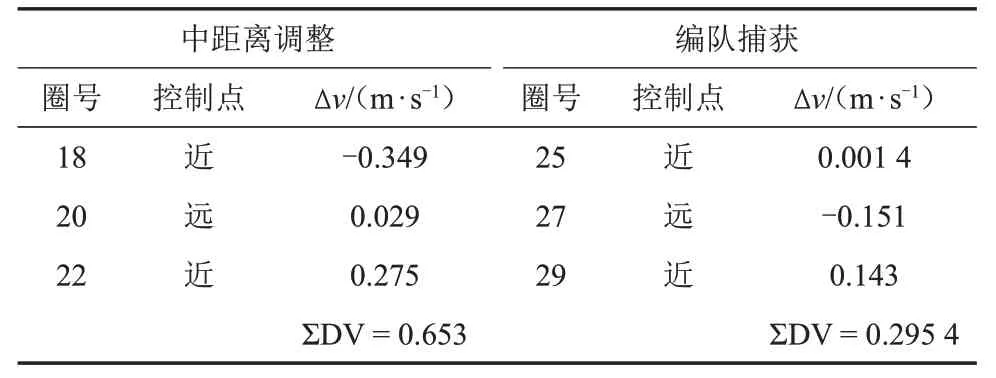
表7 中距离调整和近距离捕获的编队控制策略Table 7 Maneuver strategies of medium distance&close

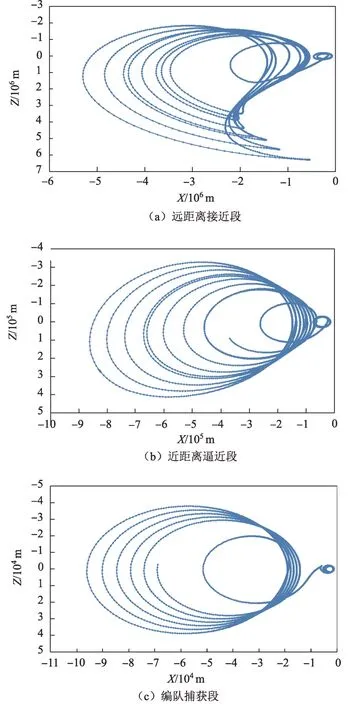
图3 3段编队飞行轨道控制的相对运动轨迹Fig.3 Formation relative motion of 3 sections

本文按照首先平面控制、其次拱线控制、然后平面内参数控制设计了顺序优化的5脉冲控制策略，通过远距离接近、中距离调整和近距离捕获的渐进式分段控制，可有效解决月球大椭圆轨道差异较大条件下渐进稳定实现近距离编队的问题。

4 结 论

为实现月球大椭圆轨道双星串行编队飞行目标，提出了基于交会控制模式，对平面、拱线、形状和相位等轨道全要素进行控制的思路。针对月球大椭圆轨道摄动、变轨演化等特点，在分析机动脉冲影响效应的基础上，设计了顺序优化的5 脉冲编队控制策略。仿真算例表明，按照远距离接近、中距离调整和编队捕获形成的分段控制思路，通过多次渐进式轨道机动调整，可实现交会终点满足跟飞编队飞行状态的目标。后续针对地面测定轨精度，卫星控制精度进一步分析该方法在实际应用中的效果。