基于改进预测滤波的小天体精确着陆自主导航方法研究

冀红霞，宗 红，黄翔宇,2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190）

引 言

小天体探测将是未来深空探测的热点之一[1]。由于深空天体与地球的距离遥远，导致地面测控站所发出的测控信息的传输出现时滞,难以实现对着陆过程进行实时测控，因此深空探测着陆任务必须利用探测器上的敏感器和导航算法自主地完成[2]。传统的惯性导航系统由于初始对准误差、常值漂移以及模型不确知参数的存在，导致导航精度较低，不能满足精确着陆的任务需要。为提高探测器导航精度，需要引入相对导航传感器直接测量探测器相对目标天体的信息。日本空间科学研究所（Institute of space and Aeronau‐tical Science，ISAS）针对MUSES-C 任务提出了利用光学测量的自主着陆小行星导航方案。该导航方案通过导航相机和激光测距仪进行测量，经过导航滤波器处理这些图像和距离信息来确定探测器的位置和速度[3]，欧洲航天局（European Space Agency，ESA）的“罗塞塔号”（Rosetta）任务利用激光测距仪与多普勒雷达确定探测器相对着陆区的高度、速度和姿态信息[4]。喷气推进实验室（Jet Propulsion Laboratory，JPL）Johnson 等[5]提出了一套基于计算机视觉的小天体软着陆导航方案，通过跟踪多帧图像特征点，结合激光高度计数据对探测器运动进行估计。

由于小天体尺寸小，形状不规则，表面性质多变，很难得到精确的探测器运动学模型，因此为了在不能精确确定引力模型和着陆地点状况的小天体表面着陆，必须有自主性强、精度高和鲁棒性强的导航算法。为了确定探测器位置、速度及姿态状态，并抑制模型误差及观测噪声与系统噪声的影响，考虑到系统的非线性，需要设计非线性滤波器。非线性估计领域最常用的方法是扩展卡尔曼滤波（Extended Kalman Filter，EKF）[6]，它具有收敛速度快、算法简单等优点。尽管EKF 在建模准确且系统噪声为零均值白噪声的情况下，可以获得良好的估计效果。但在实际应用中，难以获得精确的系统模型，且最初建好的模型在系统运行过程中受环境变化的影响可能变得不准确，进而造成模型误差，这时采用EKF 将导致滤波精度下降甚至发散。

非线性预测滤波算法（Nonlinear Predictive Fil‐ter,NPF）[7-8]对不确定模型具有适应性，该算法通过使预测输出与测量输出的误差和模型误差的加权和最小值来估计模型误差，进而修正状态估计，形成一种递推的在线估计算法，由于对模型误差实时进行跟踪，故收敛速度较慢。

针对NPF 和EKF 的局限性，本文采用改进的预测滤波方法，首先利用NPF 的预测输出与实际测量输出之间的方差最小的原则来估计模型误差并修正系统模型，再利用EKF 的时间更新和测量更新来进一步估计系统状态，并针对小天体精确着陆精度的要求，建立小天体着陆运动学模型，结合陀螺、光学相机和测速仪测量信息来确定探测器位置、速度和姿态，推导了小天体探测器软着陆系统中应用的预测滤波算法。在分析导航系统可观性的基础上，通过仿真验证在小天体引力变化引起的模型误差下的导航精度效果，并与EKF 的估计效果进行比较分析。

1 小天体探测器自主光学导航系统

1.1 小天体引力场模型

为了建立小行星探测器着陆段仿真模型，需要对小行星引力场进行建模，以模拟探测器在着陆段的运动。小行星一般都是不规则的椭球体，一般采用球谐项展开来建立其引力势函数[9]。假设小天体密度为常值，利用小天体形状模型，通过数值积分可计算出小天体引力场谐项系数[10]。式（1）给出了小天体引力势函数模型（四阶）。

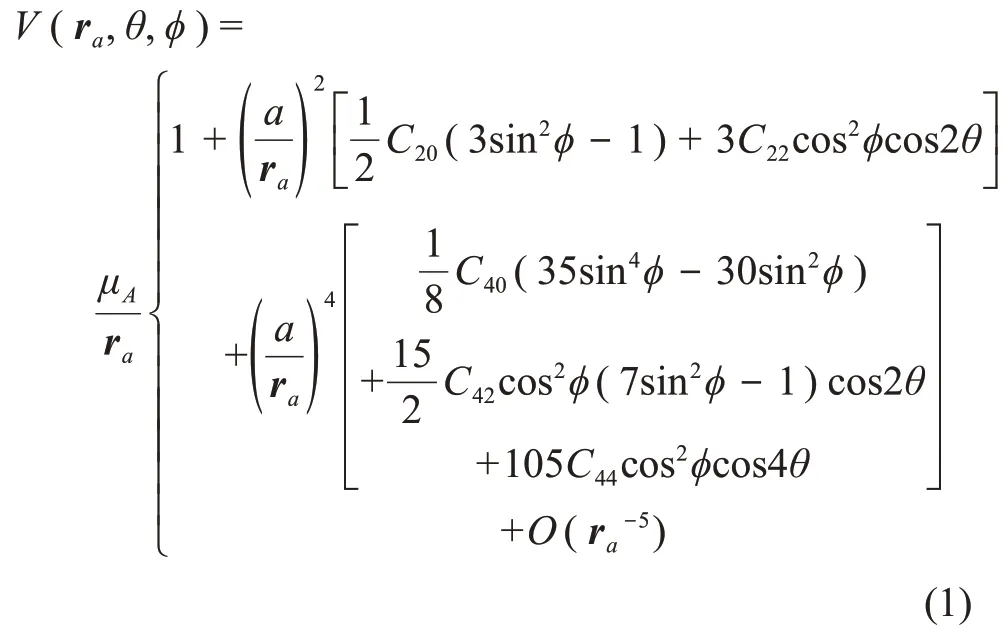
其中：μA=GM为万有引力常数和小天体质量的乘积；a为小天体的名义半径；ra为探测器到小天体质心的距离；θ,ϕ分别为赤经、赤纬；C20,C22,C40,C42,C44为小天体引力势函数调谐项系数。

小天体引力加速度分量可以表示为

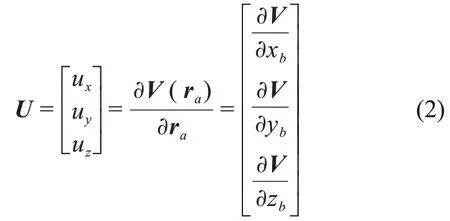
其中：下标b表示探测器三轴位置分量定义在小天体固连坐标系中。

1.2 小天体着陆运动学模型与测量模型

探测器导航的任务就是确定探测器相对于所选定的参考坐标系的位置、速度和飞行姿态，需找到一个合适的参考坐标系（参见图1）。所以这里定义了涉及到的参考坐标系：着陆点坐标系、本体坐标系和相机坐标系。

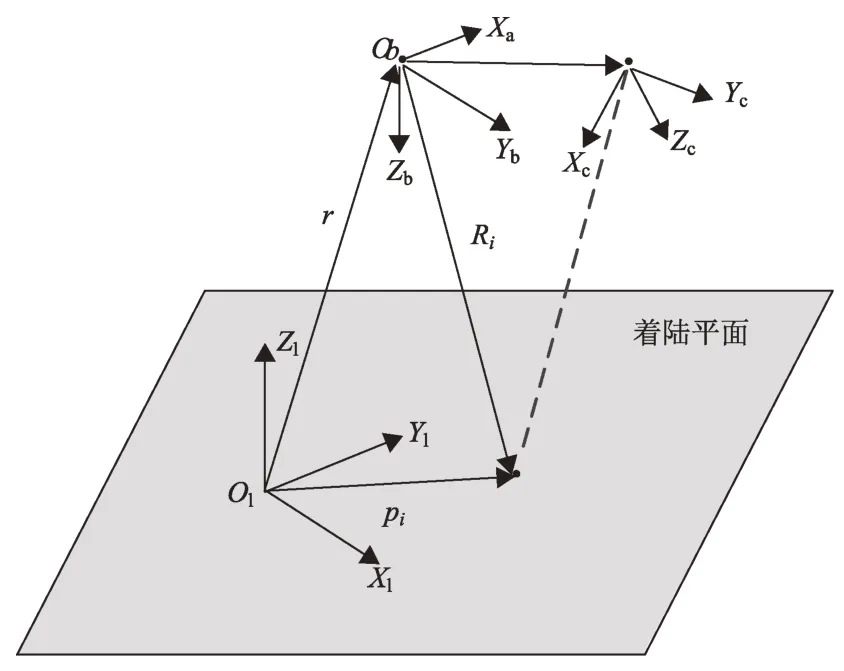
图1 坐标系相对几何关系示意图Fig.1 Relative geometric relations of coordinate system

1）着陆点坐标系{l}：原点定义为着陆点，基准平面取为当地水平面，x轴指向东，y轴指向北，z轴与x、y轴构成右手坐标系。

2）本体坐标系{b}：原点定义为探测器质心，x，y，z轴分别沿探测器3个惯性主轴方向构成右手坐标系。

3）相机坐标系{c}：原点定义为相机的光心，x,y轴平行于像平面，z轴与x，y轴构成右手坐标系。

1.2.1 小天体探测器运动学模型

利用惯性敏感器测量建立探测器着陆运动学方程为

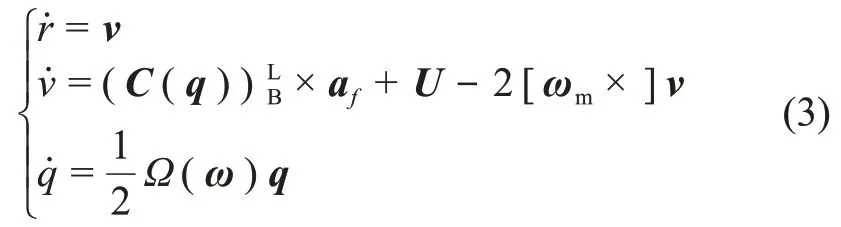
其中r和v分别为探测器在着陆点坐标系下的位置和速度；af为IMU 测量得到的加速度，ωm为小天体的自旋角速度；q为表示探测器本体系相对着陆点坐标系的姿态四元数；U为上一节提到的小天体引力加速度；(C(q))LB为本体系到着陆点坐标系的方向余 弦阵，简写为C(q)。

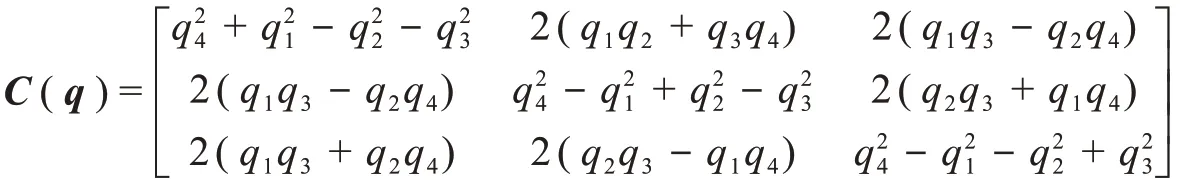
Ω(ω)定义如下

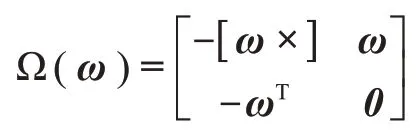
1.2.2 IMU测量模型

假设IMU 固连于着陆器体坐标系，可直接敏感着陆器相对于惯性空间的角速度和非引力加速度。则加速度计和陀螺的测量模型分别表示为

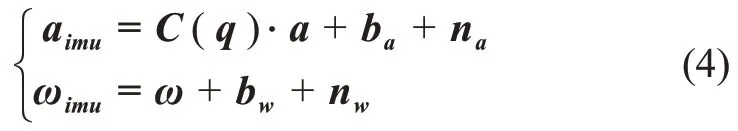
其中，ba和bw分别为加速度计零偏和陀螺零偏。

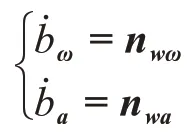
其中：a为除引力外所有作用于探测器上的合力产生的加速度，na、nw分别是加速度计和陀螺测量噪声。

1.2.3 导航相机测量模型

探测器在着陆点固连坐标系下的状态参数为(r,q)，着陆点固连坐标系下第i个特征点的位置矢量为L pi，探测器到第i个特征点的位置矢量在Σl，Σb和Σc3个坐标系下的表示分别为

1）着陆点固连坐标系Σl下的表示为

2）在探测器体固连坐标系Σb下的表示为

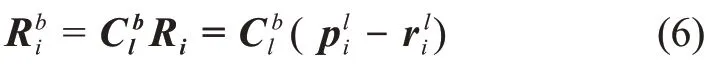
3）在相机固连坐标系Σc下的表示为

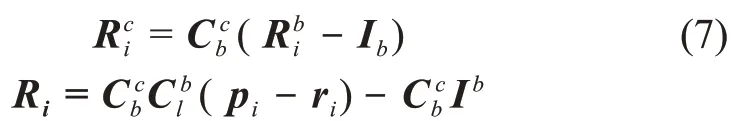
为简化问题起见，这里假设相机坐标系与探测器本体系重合，即Ib= 0，=I3×3,则探测器到第i 个特征点的位置矢量在相机坐标系下的表示为

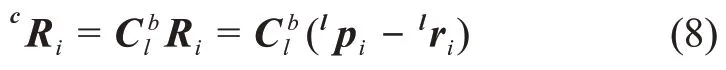
假设光学导航相机模型为理想的小孔成像模型，由射影变换可得

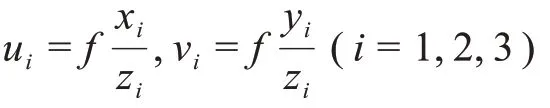
其中：[xiyizi]T是相机固连系下探测器到第i个（i = 1,2,3）特征点的位置坐标，跟踪的特征点在像平面中的位置坐标即为导航测量量，可表示如下

其中；m为为像素；[ui,vi]为成像平面上的像元像素坐标值，坐标mi=[uivi]T=f[xi/ziyi/zi]T。

则导航测量方程为

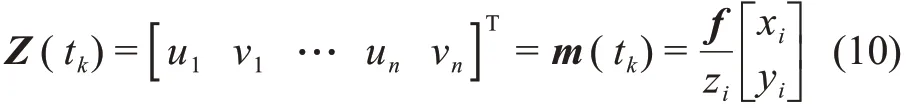
1.2.4 测速敏感器测量模型

测速敏感器输出的相对速度的测量方程[11]如下

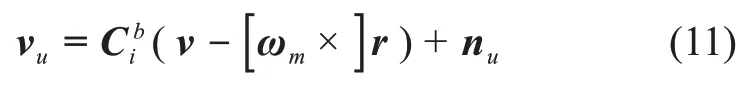
其中，nu为测速敏感器测量噪声。

2 基于预测滤波的小天体探测器自主光学导航系统

2.1 状态方程

导航系统状态包括探测器当前位置、速度和姿态以及成像时刻探测器位置和姿态，即

其中：xE为系统当前状态；和分别为成像时刻探测器位置和姿态，其不随时间变化，当生成新图像时由新图像成像时刻探测器位置和姿态代替前一图像成像时刻探测器位置和姿态作为系统状态。

估计状态为

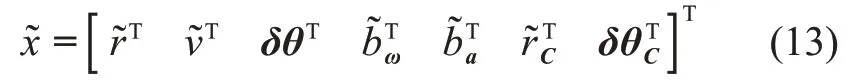
线性化式（3）可得系统当前误差状态方程如下

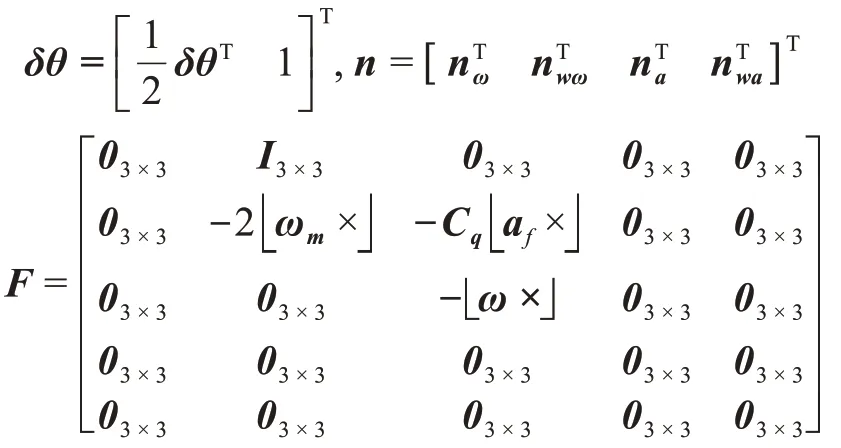
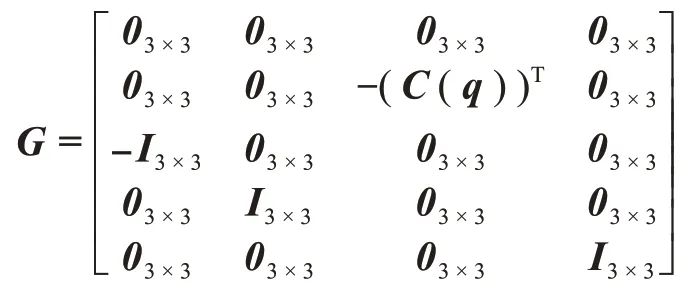
假设k 时刻相机拍摄一幅图像，则状态方程xE|k和协方差PEEk|k分别扩维为xk和Pk|k。

其中

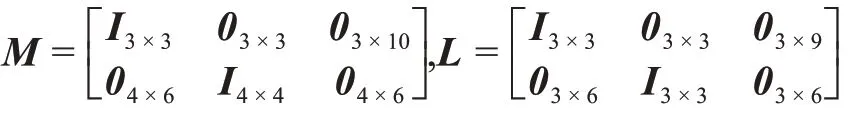
2.2 观测方程

对于导航相机，以特征点在像平面的位置为观测量，对于特征点由式（10）可得观测方程为

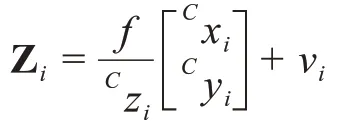
其中：vi为观测噪声，设其协方差阵为Rv。第i时刻导航陆标pj估计观测量为

则第i时刻的观测量残差为

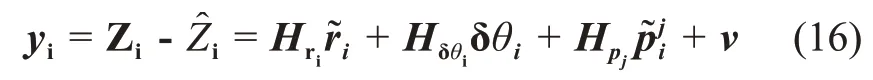
测量方程为

其中：H1=[H1103×3H1303×303×3]

其中

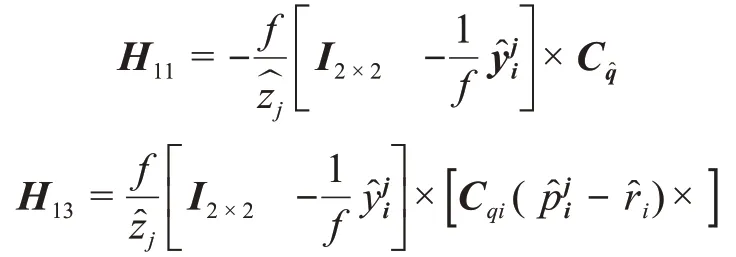
对于测距测速敏感器，由（11）可得观测方程为

其中测量敏感矩阵为

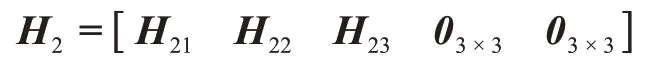
其中

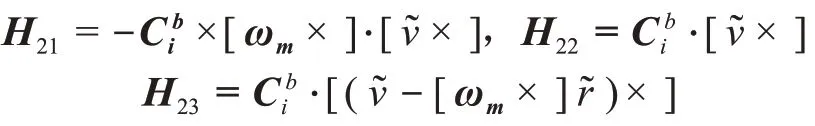
2.3 小天体探测器自主导航滤波器

2.3.1 预测滤波算法基本原理

设一个非线性系统方程为

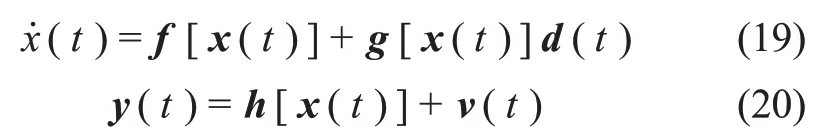
其中：x(t)∈是状态向量；f∈是模型向量 ；d(t)∈是模型误差向量；g∈是模型误差扰动矩阵；h∈是测量向量；y(t)∈是测量输出向量；v(t) 是零均值的高斯白噪声，其方差阵R ∈。将输出估计方程泰勒展开，并运用李导数知识，得

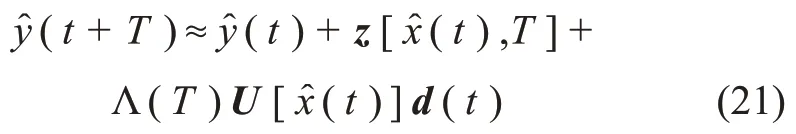
其中：T为时间间隔；z[(t),T]的第i个元素为

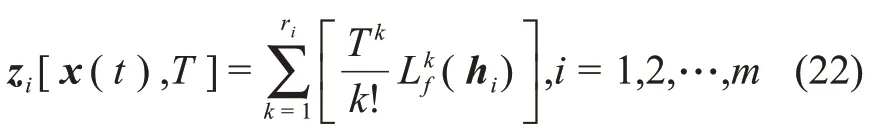
其中：ri是与第i个输出对应的相对阶，为d(t)出现在hi[x(t)]的微分中的最低阶数；Λ(T)∈是对角矩阵，对角元λii=Ti/ri!,i=1,2,…,m；U(x)∈为灵敏度矩阵。

基于预测输出与实际测量输出的残差最小的思想来估计系统的模型误差。由此建立的目标函数是由测量输出与预测输出间残差以及模型误差修正项的加权平方和组成的，即

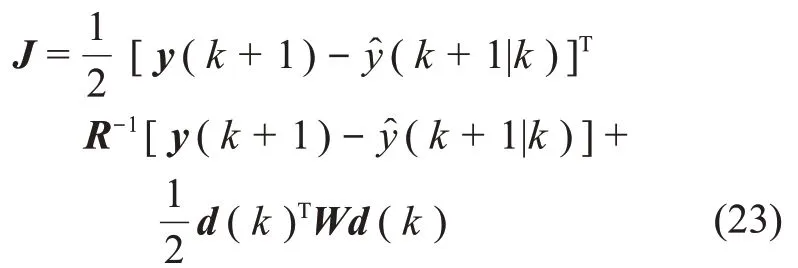
其中：括号中的k表示第k个采样时刻；y(k+ 1)是t(k + 1)时刻的测量输出。预测输出为

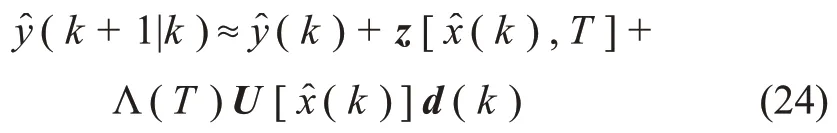
将（24）式代入（23）式，并令∂J/∂d(k)= 0，可得模型误差估计为

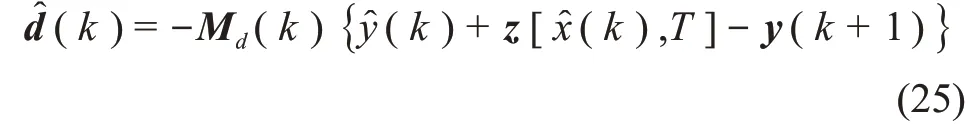
其中

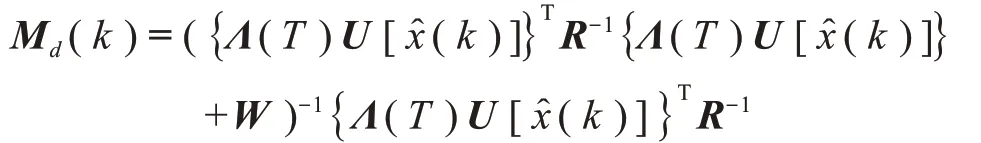
2.3.2 改进的预测滤波算法

基于预测滤波原理，并针对探测器自主光学导航系统运动学、运动学模型和测量噪声的非线性特性，以及小天体模型中存在的引力参数不确定性，将NPF与EKF 进行结合，在状态方程中引入模型误差，将探测器的位置、姿态和四元数作为状态变量，使用测速敏感器和光学相机的测量值，求得探测器的位置、速度和姿态的估计值。

为了表达方便，将同时考虑模型误差和过程噪声的非线性系统的状态方程写成如下形式

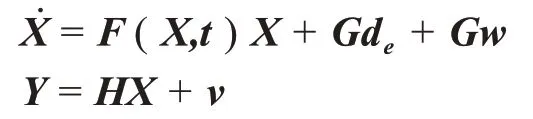
令采样时间间隔为T，预测滤波和扩展卡尔曼滤波相结合的滤波步骤如下：

1）由（25）式计算模型误差d(k)；

对于2.1节、2.2节组成的导航系统进行推导，灵敏度矩阵U、对角阵Λ(T)和在预测输出时用到的z[(t),t,T]的计算公式分别如下

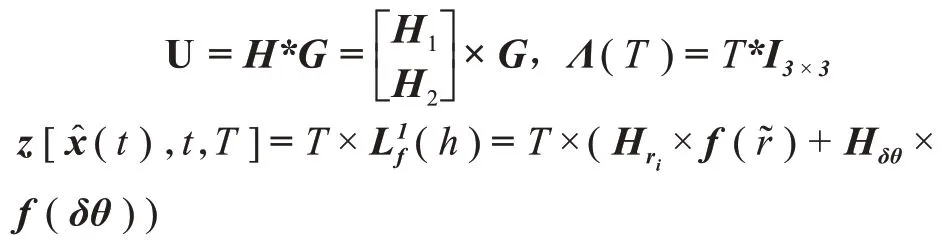
2）将d(k)代入一步预测估计值中

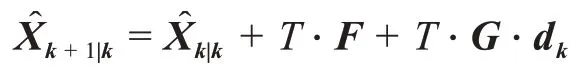
3）由EKF计算滤波值为

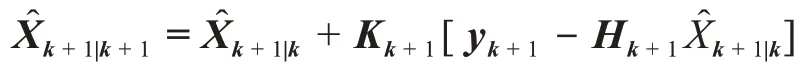
4）计算滤波增益阵

5）一步预测方差阵为

估计方差阵为

2.4 导航系统的可观性分析

测量系统的可观性，反映系统通过测量在有限时间内的观测量确定系统状态的能力。导航系统的基本任务就是确定航天器的位置和速度，所以判断导航系统能否满足任务要求的第一步，就是分析其可观性。为了分析导航系统的可观性，这里引入非线性系统局部弱可观的概念[12-13]。

定义1：如果对于定义区间内的每个X,系统Σ 都局部弱可观，那么称系统Σ局部弱可观。记系统Σ的观测矩阵为

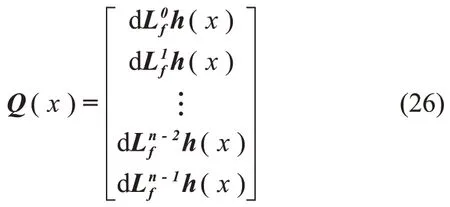
其中：n为状态向量X的维数；(X)为k阶李导数。

定义2：如果rank(Q(X0))=n，那么称系统Σ在X0点满足可观性秩条件。

这里利用非线性系统的可观性秩条件来分析自主导航系统的可观性。

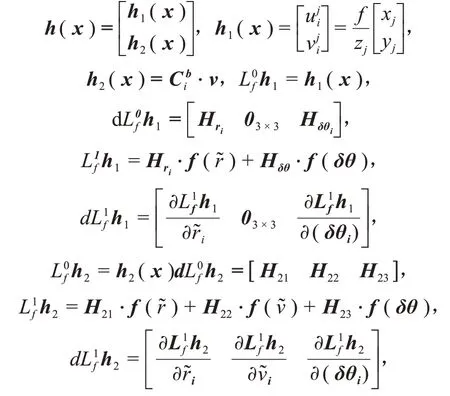
容易看出，的具体表达式将非常复杂，所以，观测矩阵的数学表达式也非常复杂，但是，已可决定Q的秩，且rank(Q0)= 9，故在此将不再计算，且定义。

需要估计的参数维数m= 9（位置、速度和姿态信息），由上述分析可知rank(Q0)= 9，根据定义2可得，对应的导航系统在X0点是局部弱可观的。

3 仿真结果

3.1 仿真验证

为验证本文提出的采用预测滤波的小天体探测自主光学导航系统的有效性和可行性，取小行星Eros433作为目标天体进行数学仿真，Eros433小天体物理参数如表1所示。

表1 仿真分析参数列表Table 1 The parameter list of simulation analysis

仿真初始条件为位置各方向存在50 m 的随机误差，速度各方向存在1 m/s 随机误差，姿态各轴指向存在1°的随机误差，导航陆标位置各方向存在1 m随机误差，测速仪各方向存在0.01 m/s随机误差。设导航相机焦距为3.5 mm，导航相机和测速仪以1 s的采样间隔输出，图像处理精度为1个像素，仿真采用模拟陆标进行。探测器在着陆过程中采用Apollo多项式制导方法，仿真初始状态如表2所示，陀螺相关参数和加速度计相关参数如表3～4 所示，状态误差协方差阵初值P0= 103⋅I15×15。

表2 探测器仿真初始状态Table 2 The initial simulation state of the detector

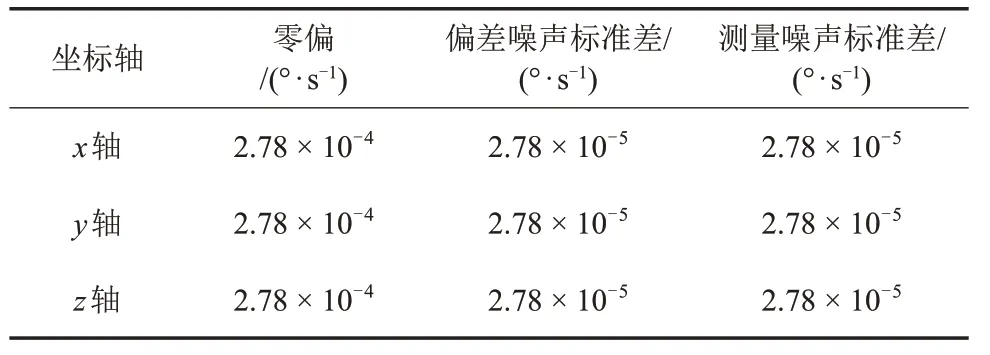
表3 陀螺相关参数Table 3 The parameters of the gyros

表4 加速度计相关参数Table 4 the Parameters of the Accelerometers

在上述设定参数下，采用改进的预测滤波算法的仿真结果如图2（a）和（b）所示。从图2 中的仿真结果可以看出，使用改进的NPF 算法较EKF 实时性更好，位置、速度和姿态曲线收敛速度与EKF 相比更快趋于收敛，且具有较高的导航精度。

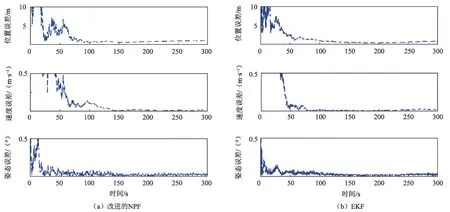
图2 改进的NPF和EKF滤波曲线Fig.2 The filter curve of improved NPF and EKF

3.2 误差分析

由于滤波模型中的小天体参数存在不确定性，这里假设小天体引力场模型存在x%的不确定性（x=20,50，100），进行了仿真，给出了导航滤波的误差值，结果分别如下图所示：图3～4 为模型参数存在20%不确定度时的滤波误差，图5～6 为模型参数存在50%不确定度时的滤波误差，图7～8 为模型参数存在100%不确定度时的滤波误差。

为研究不同模型误差对导航精度的影响，此处引入均方根误差（Root Mean Squared Error，RMSE）为评价指标，均方根误差按下式计算

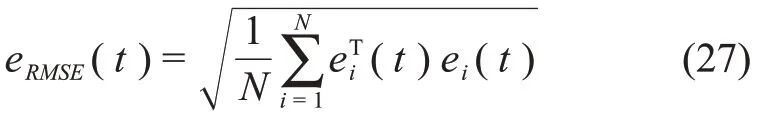
其中：N为仿真次数，本节仿真中取N= 10；ei(t)为第i次仿真得到的状态误差。表5 给出了不同模型误差下由10 次Monte Carlo 仿真得到的着陆器各状态分量在仿真结束时刻的平均估计误差。

从表5～6仿真数据和图3、图5和图7可以看出，随着模型误差的增大，EKF 的估计误差也随之增大。而图4、图6 和图8 改进的NPF 的误差增加幅度却不明显，这是由于EKF 只针对白噪声的模型误差进行处理，导致精度下降，而改进的NPF 对模型误差做一步估计并进行补偿，不限制模型误差的类型，从而提高了估计精度。由此验证了NPF 对模型误差的估计和补偿的有效性。

1）当存在20%误差不确定度时：

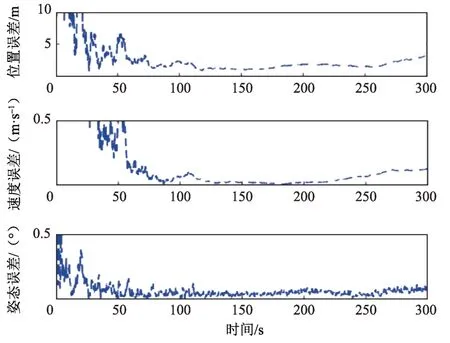
图3 EKF滤波精度Fig.3 The accuracy of EKF

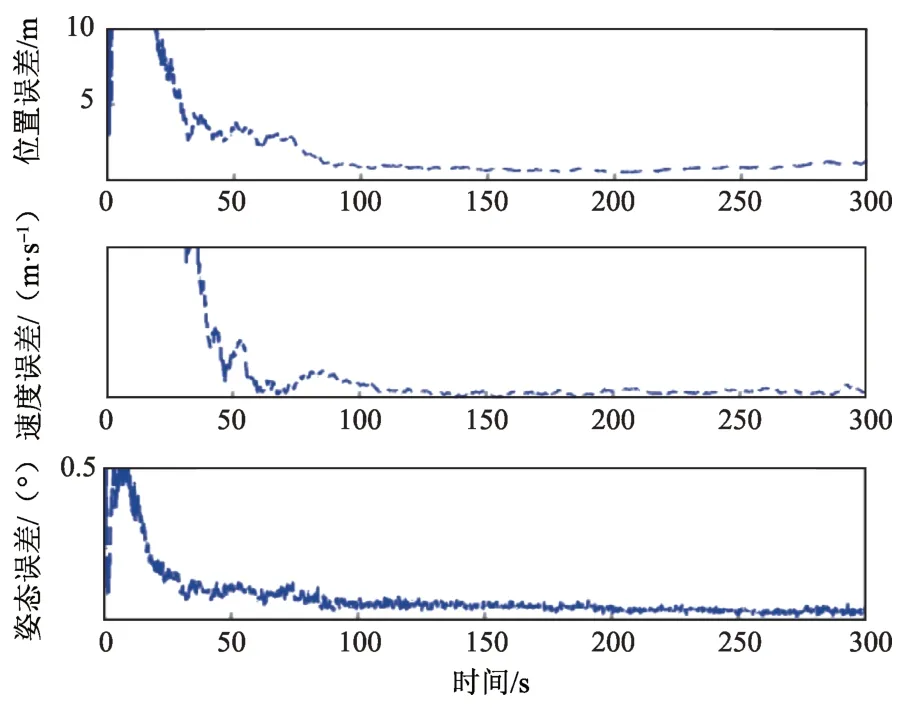
图4 改进的NPF滤波精度Fig.4 The accuracy of improved NPF

2）当存在50%误差不确定度时：

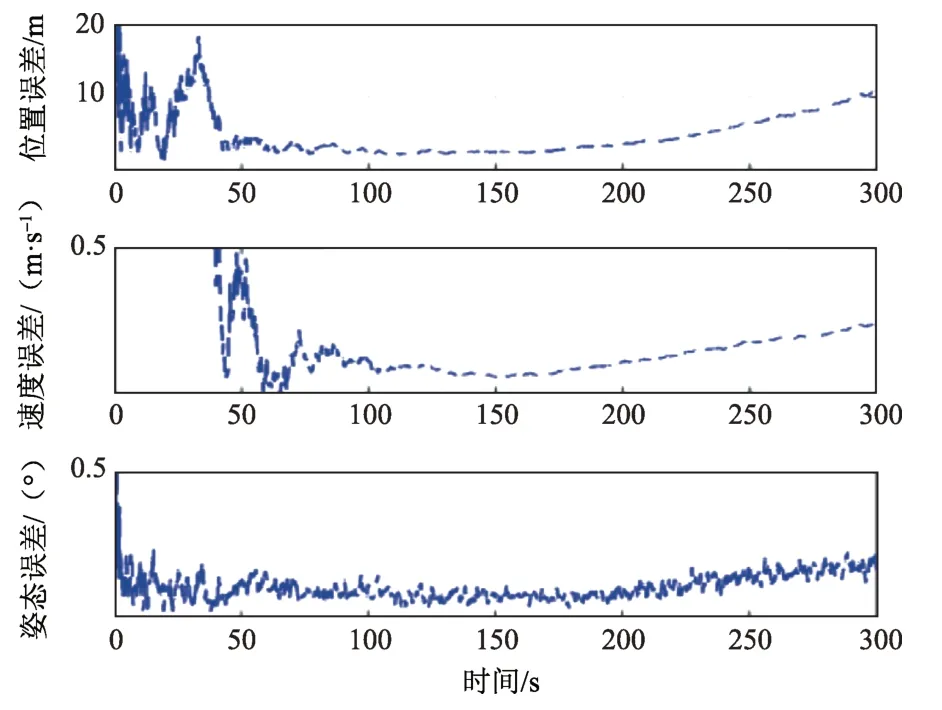
图5 EKF滤波精度Fig.5 The accuracy of EKF

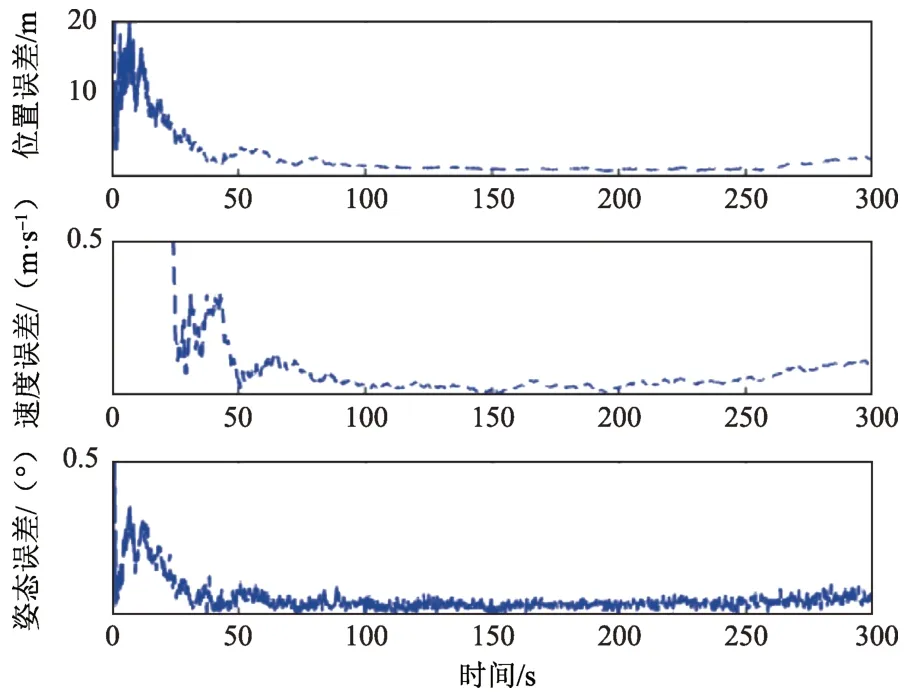
图6 改进的NPF滤波精度Fig.6 The Accuracy of improved NPF

3）当存在100%误差不确定度时：

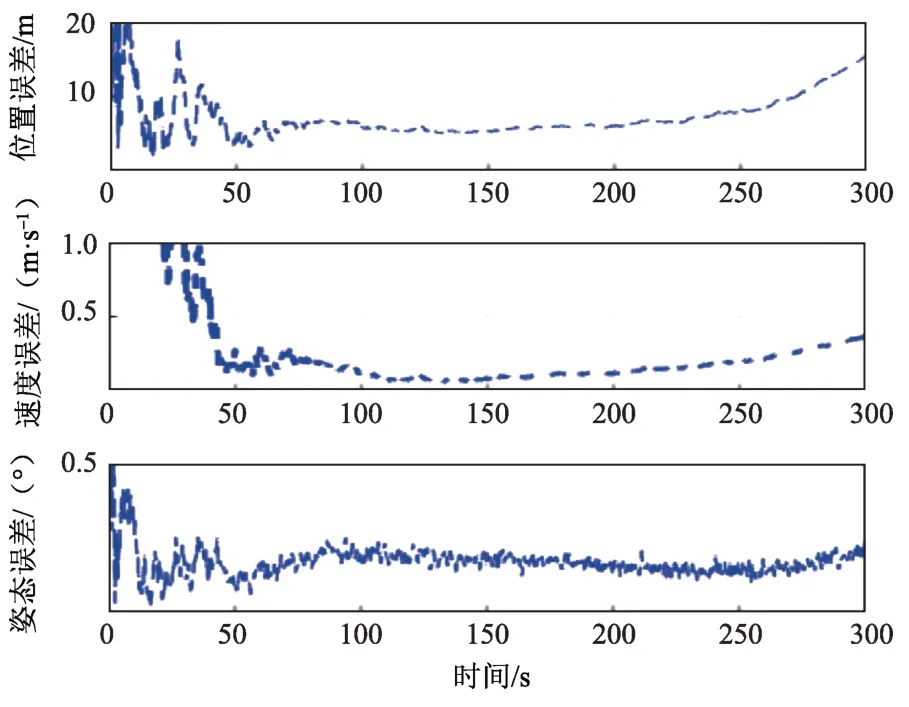
图7 EKF滤波精度Fig.7 The accuracy of EKF

图8 改进的NPF滤波精度Fig.8 The accuracy of improved NPF

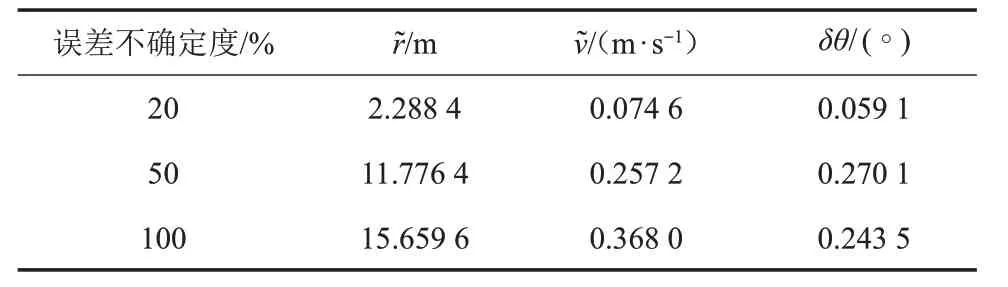
表5 不同模型误差下EKF蒙特卡罗导航误差Table 5 The Monte Carlo navigation errors under different model error of EKF

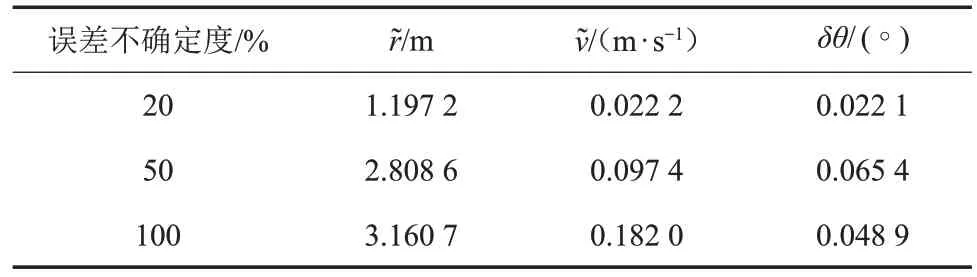
表6 不同模型误差下改进的NPF蒙特卡罗导航误差Table 6 The Monte Carlo navigation errors under different model error of improved NPF

4 结 论

本文提出了一种用于探测器着陆小天体的光学自主导航滤波方法，该方法首先在惯性导航加测速修正的基础上，将光学成像敏感器加入到导航系统。通过下降过程中拍摄天体表面陆标图像以获得着陆器相对陆标的方位信息，在进行状态估计是采用基于预测滤波与扩展卡尔曼滤波相结合的滤波器，并通过仿真验证了在存在较大模型误差时，改进的预测滤波方法可以有效地估计探测器的位置和速度信息，且算法对模型不确定性具有一定的适应性，可适应小天体复杂多变的环境。