基于改进弧段切点弦的多椭圆检测
张鹏,季爱明
(苏州大学 轨道交通学院,江苏苏州 215100)
椭圆检测是图像处理中的一个重要技术。椭圆检测被广泛应用于相机校准[1]、工业零部件检测[2]、细胞检测[3]、瞳孔识别[4]等领域。而在实际应用中,图像中往往存在多个待检测的椭圆,因此,多椭圆检测具有十分重要的研究价值。
椭圆检测算法大致可以分为三类:基于霍夫变换的方法[5-6]、基于最小二乘的方法[7]和基于弧段提取的方法。
霍夫变换方法往往计算量过大,运行时间较长。最小二乘方法则对噪声较为敏感。这两种方法均是基于边缘点来检测椭圆,忽视了边缘的连续性,且不太适用于多椭圆的快速检测。基于弧段提取的方法则从边缘段出发,寻找属于同一椭圆的弧段组,通过弧段组检测目标,能有效实现多椭圆的快速、高精确度检测。文献[8]利用梯度信息与凹凸性将弧段分类到四个象限,组合不同象限的弧段,利用椭圆弧段间的位置关系和椭圆中心应与平行弦中点共线的特点筛选弧段组以检测椭圆。文献[9]同样将弧段分类到四个象限,并基于椭圆内包多边形为凸多边形的性质对弧段组进行筛选。弧段组筛选效果越好,基于弧段进行多椭圆检测的效果越好。因此,如何快速准确地筛选弧段组是基于弧段提取检测多椭圆方法的关键点。
为了提高图像中多椭圆检测的精确度,该文在弧段分象限的基础上提出了基于改进弧段切点弦的多椭圆检测算法。使用弧段切点弦方法计算弧对椭圆中心,筛选弧段组。为了减小切点数字化误差对中心计算的影响,一方面在弧对上多次取不同切点计算多个椭圆中心坐标,然后采用中值滤波;另一方面使用抑制数字化误差影响的弧段切线斜率估计方法估计弧段上点的切线斜率。最后,通过实验验证了该文方法的性能。
1 弧段分象限检测
弧段分象限检测首先对输入图像进行边缘检测,提取物体边缘轮廓;然后结合边缘点梯度信息和弧段凹凸性将边缘弧段按象限分为四类;再对由不同象限弧段组成的弧段组合进行筛选;拟合筛选后的弧段组;验证并聚类候选椭圆。
筛选弧段组时常用位置约束和中心约束方法。中心约束筛选时通过弧段组构造两个弧对,计算每个弧对的椭圆中心。基于切点弦计算椭圆中心的示意图如图1 所示。在弧段αa上取两个相异点P1、P2,过该两点作切线交于点Pa,连接P1、P2构成弦P12,连接Pa与弦P12中点的直线经过椭圆中心。同理,在另一条弧段上也能得到经过中心的直线。两直线交点即为弧对的椭圆中心。

图1 基于切点弦计算中心示意图
切点弦方法简便、易于计算,但它的精确度易受边缘切点数字化误差的影响。对此,该文对切点弦方法作出了改进。
2 切点弦弧段筛选
首先通过椭圆两个相邻象限弧段间的位置关系初步筛选出弧段组[10]。然后通过弧段组τabc构造两个弧对(αa,αb)和(αb,αc),利用弧对的中心约束进一步筛选弧段组。
基于切点弦计算弧对中心的方法只计算单个中心,易受边缘切点数字化误差的影响而出现较大偏差[11],从而影响弧段筛选的准确度。为了降低边缘切点数字化误差对弧段筛选的影响,该文对切点弦弧段筛选算法作出了改进。改进的切点弦弧段筛选算法如算法1 所示。
算法1:改进的切点弦弧段筛选算法
输入:三个弧段的边缘点集Pa、Pb、Pc;中心数Ns。
输出:若弧段组τabc满足中心约束则输出true,不满足则输出false。

该算法多次从弧对的两个弧段上取不同切点计算过中心线,由多对过中心线计算得到多个椭圆中心坐标,然后采取中值滤波的方法减小数字化误差的影响。实验表明中心坐标数Ns取6 时可以较好地平衡精确度和时间。为了使切点的寻找范围尽可能大,从弧段的中点处开始向左右两端取切点计算过中心线。计算两个弧对中心Cab(xab,yab)和Cbc(xbc,ybc)的欧式距离discenter。如果discenter小于阈值Thcenter,则该弧段组满足中心约束,认为该弧段组的三个弧段属于同一个椭圆。Thcenter取M×N×0.05[8],M×N为图像大小。
3 抑制数字化误差弧段切线斜率估计
切线斜率估计如图2 所示。

图2 切线斜率估计
如图2 所示,对于椭圆上的点P0(x0,y0),设以P0为圆心,R为半径的圆与椭圆交点为P1(x1,y1)、P2(x2,y2),P1为左交点,P2为右交点。用直线P1P2的斜率来近似P0处的切线斜率m0。的计算公式如式(1)所示:

为了使足够近似m0,R的取值有上限约束,如式(2)所示[12]:

其中,Δθmax为P1与P0的离心角最大差值,b为椭圆短半轴长。Δθmax取π10,则有R≤0.174 3b。此外,受边缘点数字化误差的影响,实际计算出的与理论值之间存在误差,可以用实际计算出的切线与理论切线间的角度差∂φ衡量该误差[13]。设P1、P2坐标的数字化误差为Δx1、Δy1、Δx2、Δy2,变化范围在±0.5 之间,则∂φ如式(3)所示:

基于Δx1、Δy1、Δx2、Δy2所能取的最大、最小值对∂φ的公式进行讨论,可得到误差最大值∂φmax如式(4)所示:
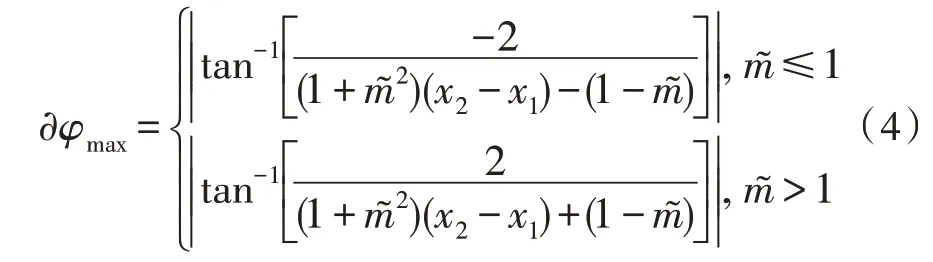
由式(4)可以看出,(1+2)(x2-x1)越大,则∂φmax越小。直线P1P2的方程如式(5)所示:

点P1、P2的欧式距离公式如式(6)所示:

将式(5)代入式(6)可得式(7):

所以,P1P2的距离越大,∂φmax越小。而R值越大,P1P2的距离越大。因此,R值越大,∂φmax越小。当R取0.174 3b时,∂φmax最小。
因为椭圆短半轴长b无法预先得知,所以该文基于椭圆的最小外接矩形估计短半轴长。如图3 所示,椭圆最小外接矩形的宽等于椭圆的短轴长。对弧段组(αa,αb,αc)提供的点集,使用旋转卡壳法找到弧段组的最小外接矩形,根据该最小外接矩形的宽估计短半轴长。由于弧段组中各个象限的弧段可能因为噪声而并不完整,由弧段组找到的最小外接矩形可能略小于完整椭圆的最小外接矩形。因此,估计的短半轴长等于或略小于实际的椭圆短半轴长b,使得R值可能略小于0.174 3b,从而使得∂φmax比理论可取的最小值稍大,但确保了可以足够近似m0。

图3 椭圆最小外接矩形
基于误差分析选取合适R值的抑制数字化误差影响的弧段切线斜率估计算法如算法2 所示。
算法2:抑制数字化误差影响的弧段切线斜率估计算法


4 实验与分析
为了验证该文算法的性能,通过在Matlab 平台上编程来实现该算法。首先使用自适应Canny 边缘检测器检测边缘点;然后利用梯度信息与弧段凹凸性将边缘弧段分类到四个象限;选取三个象限的弧段构成弧段组后,使用位置约束和基于改进弧段切点弦方法的中心约束进行筛选;对筛选出的弧段组用最小二乘法进行拟合;最后对拟合出的候选椭圆进行验证和聚类。
实验使用的数据集为虚拟图像集Dataset #1 和真实图像集Prasad 数据集。Dataset#1 数据集为100张600×600 像素的虚拟图像,其中,包含残缺椭圆和遮挡椭圆。Prasad 数据集为椭圆检测常用数据集,包含198 张真实图像,图片大小为170×138 像素到800×540 像素。实验评价标准为椭圆检测常用的精确度P、召回率R、F 值和运行时间T,时间单位为s。P、R、F 值计算如式(8)-(10)所示:

其中,Ψ 为检测到的椭圆个数,γ为检测出的真实椭圆个数,Ω为图像中的真实椭圆个数。当检测到的椭圆与真实椭圆的重叠面积比大于0.8时,视为真实椭圆。
在计算弧对中心坐标时,弧段中心个数Ns越大,最终的中心坐标精确度越高,使得检测算法的精确度越高,但也会增加算法的计算时间。为了选取合适的Ns值,从Prasad 数据集中选取了50 幅图像,测试Ns对F 值和时间的影响,如图4-5 所示。

图4 Ns 对F 值的影响
由图4、图5 可以看出,随着弧段中心个数Ns的增大,时间在不断增加,而当Ns大于6时,对F 值的提升变得微弱。因此,Ns取6 时可以较好地平衡算法的精确度和时间。

图5 Ns 对时间的影响
为了对比算法的检测效果,在Matlab平台上复现了其他几种基于弧段的算法,并与该文算法进行比较。实验结果如表1-2所示,实验对比图如图6所示。
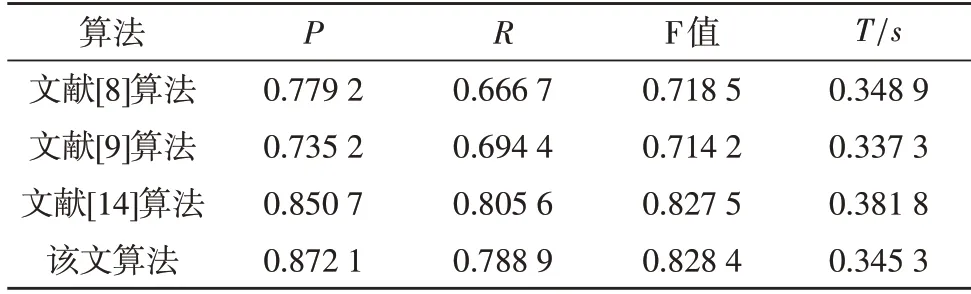
表1 Dataset#1数据集上的对比结果

图6 Prasad数据集上的对比图
从表1 可以看出,在Dataset #1 数据集上,与文献[8]算法相比,该文算法在P、R、F 值和运行时间上都取得了更好的效果。与文献[9]算法相比,虽然运行时间增加了2.4%,但是P提高了13.7%、R提高了9.5%,F 值提高了11.4%。与文献[14]算法相比,虽然R损失了1.7%,但是P提高了2.1%,F 值提高了0.09%,运行时间减少了9.6%。因此,综合考虑可知,该文算法性能更好。
从表2可以看出,在Prasad数据集上,与文献[8]算法相比,该文算法在P、R、F 值和运行时间上都取得了更好的效果。与文献[9]算法相比,虽然运行时间增加了0.8%,但是P提高了12.3%、R提高了2.3%,F 值提高了4.6%。与文献[14]算法相比,虽然R损失了3.0%,F 值损失了1.9%,但是P提高了4.8%,时间上减少了18.4%。因此,综合考虑,该文算法性能更好。

表2 Prasad数据集上的对比结果
5 结论
为了提高图像中多椭圆检测的精确度,该文提出了基于改进弧段切点弦的多椭圆检测算法。改进了基于弧段切点弦计算弧对中心的方法,计算多个椭圆中心坐标,然后使用中值滤波。使用抑制数字化误差影响的弧段切线斜率估计法计算切线。有效减小了切点数字化误差对弧对中心计算的影响。实验表明,该方法有效提高了图像中多椭圆检测的精确度,能快速有效地检测出多椭圆图像中的目标。

