基于立德树人的复习课教学——以复习“全等三角形”为例

☉安徽省安庆市开发区实验学校 秦 奋

一、学情分析

全等三角形是研究几何中角、线段相等的重要工具，判定三角形全等的方法是研究角、线段相等的常用方法，三角形全等的应用是中考考查考生时必关注的一种能力.学生的知识零散地存储在记忆中，这些知识点之间尚未建立一定的逻辑联系，学生的逻辑推理能力尚未健全，尚不能在全局上、宏观上驾驭和调控解题推理，时会时不会，得分增添了太多的偶然性.本节课从学生的心理特点、认知水平、思维方式和考前状态出发，既立足于基础，又螺旋拔高，兼顾了中等及中等以上学生的发展.

二、复习目标

（1）了解全等三角形的概念，掌握两个三角形全等的条件.

（2）建立本章的知识网络，应用相关知识解决实际问题.

（3）在图形变换中，挖掘隐含条件，能熟练地找出全等三角形，关注学生逻辑思维能力、直观想象能力、解题能力的培养，实现立德树人的目标.

（4）鼓励学生积极主动地参与到教学活动中，感受运用数学知识解决实际问题的乐趣，获取成功的激励，增强学生复习迎考的信心.

三、范例设计

1.知识梳理

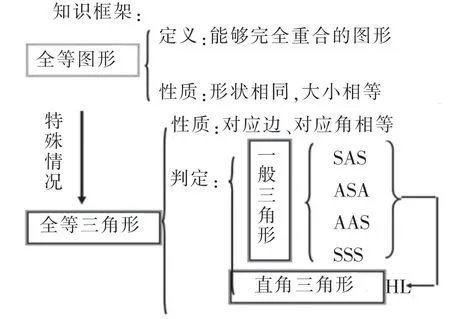
图1

例题：如图2，请你选择合适的条件填入空格内，使△DEF△DGF.

（1）因为DF=DF，___________，___________，根据SAS，可知道△DEF△DGF.

（2）因为___________，DF=DF，___________，根据ASA，可知道△DEF△DGF.

（3）因为___________，___________，DF=DF，根据AAS，可知道△DEF△DGF.

（4）因为DF=DF，___________，___________，根据SSS，可知道△DEF△DGF.

（5）若∠E=∠G=90°，___________，DF=DF，根据HL，可知道Rt△DEFRt△DGF.

设计说明：教师引导学生回顾三角形全等的相关知识.梳理本章知识结构，以例题为切入点，引导学生灵活选择不同条件下三角形全等的判定条件，既厘清了学生对知识的系统性理解，又加强了学生学习能力的训练.

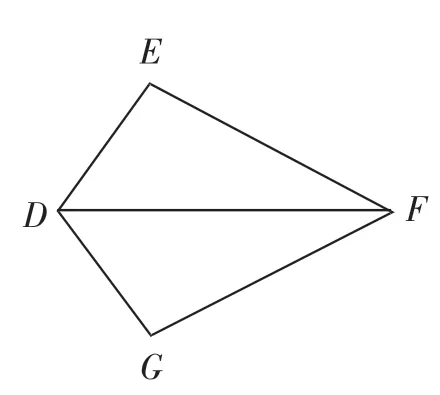
图2

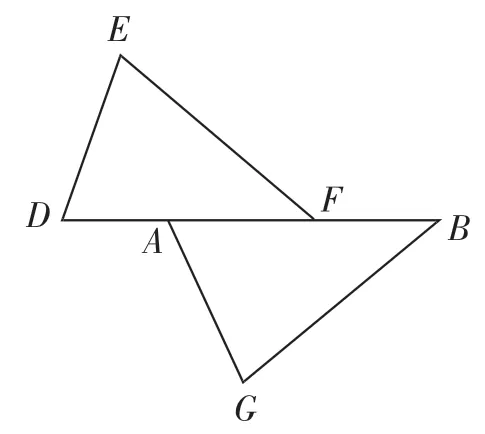
图3

2.例题呈现

如图3，若△DEF AGB，你能得到哪些结论？

变式1：如图4，若AC⊥BC，AD⊥BD，垂足分别为C、D，AC=BD，△ABC △BAD吗？为什么？

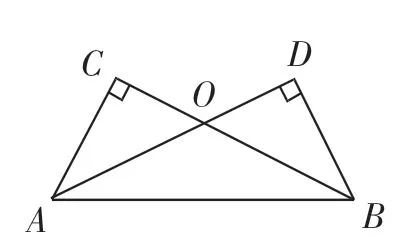
图4

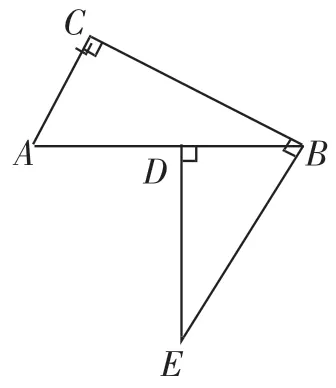
图5

变式2：如图5，AC⊥BC，ED⊥BD，BE⊥BC，垂足分别为C、D、B，AB=BE.试探究BE与AC+AD的关系.

变式3：如图6，AC⊥BC，AD⊥BD，垂足分别为C、D，AD=BC.

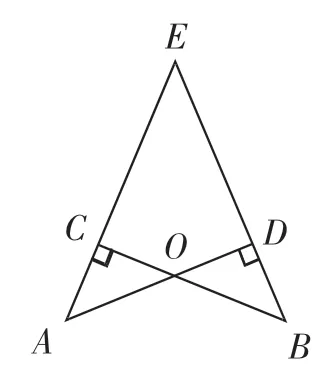
图6

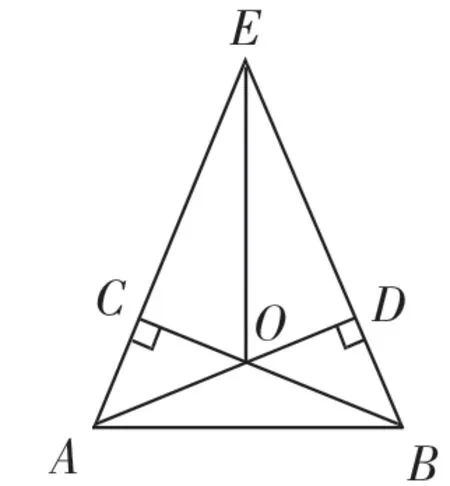
图7

（1）AE=BE吗？请说明你的理由.

（2）如图7，在上述条件不变的情况下，连接AB、OE，请判断AB与OE的位置关系，并说明你的理由.

设计说明：通过呈现变式，展示问题的共性与变化.在题组解题思路的分析过程中，达到强化知识点的目的，渗透逻辑思维素养的培养.在教学中，教师应围绕试题与解题两个角度组织学生交流讨论，激活思维.

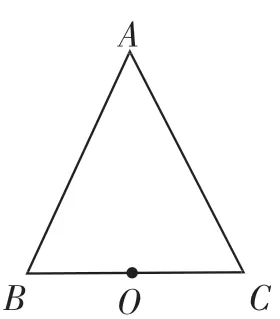
图8

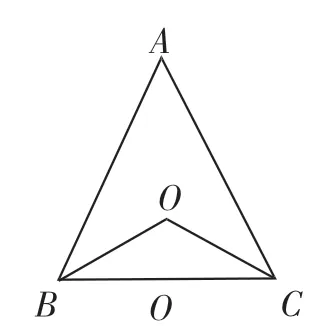
图9

3.中考题赏析

已知：点O到△ABC的两边AB、AC所在直线的距离相等，且OB=OC.

（1）如图8，若点O在BC上，求证：AB=AC；

（2）如图9，若点O在△ABC的内部，求证：AB=AC；

（3）若点O在△ABC的外部，AB=AC成立吗？请画图表示.

设计说明：本题是安徽省中考题，考查的知识点主要是三角形全等的判定方法的运用和分类讨论的数学思想.教师要引导学生分析题意，严密证明，写出规范的证明过程，达到再次强化基础、训练技能的目的.尤其是第（3）题，该题对学生的作图能力有较高的要求，教师在复习时应该予以强调，对相关知识之间的联系与规律也要高度重视，增强知识迁移能力，使不同的学生有不同的收获，达到数学学科立德树人的目的，让学生感受成功的喜悦.

4.精选练习

练习1：如图10，给出下列四组条件.

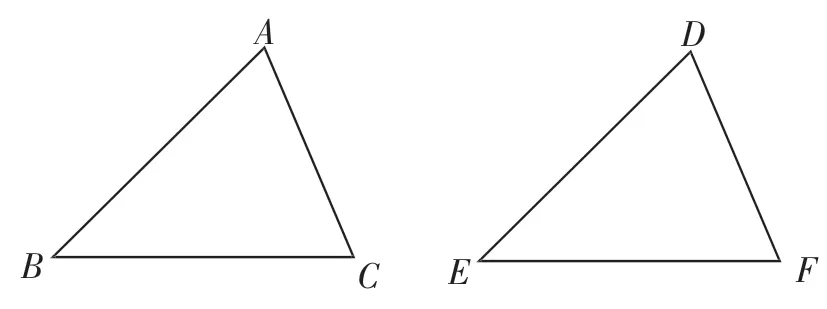
图10

①AB=DE BC=EF AC=DF

②AB=DE ∠B=∠E BC=EF

③∠B=∠E BC=EF ∠C=∠F

④AB=DE AC=DF ∠B=∠E

练习2：如图11，△ABC中，D是AB的中点.将△ABC沿DE所在直线翻折，使点A恰好落在BC上的点F处.若∠B=50°，则∠BDF=______，∠ADE=___________.

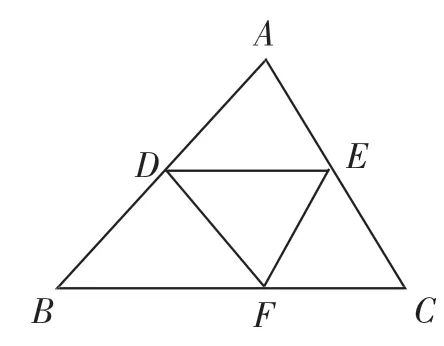
图11

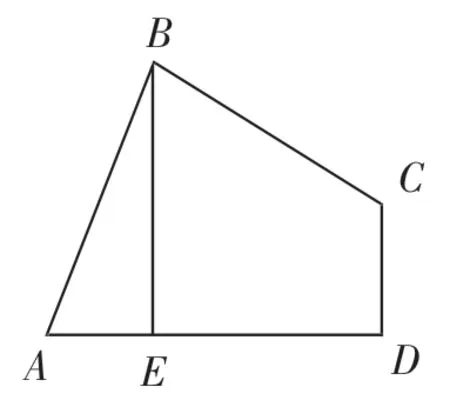
图12

练习3：如图12，四边形ABCD中，AB=BC，∠ABC=∠CDA=90°.BE⊥AD于点E，且四边形ABCD的面积为8，则BE=___________.

设计说明：根据本节课的复习内容，设置针对性强的练习，让学生在实战训练中得以巩固和提高，并通过有梯度的练习逐步拉伸学生的思维深度，提升解题能力.

四、教学思考

1.重视基础知识和基本技能

在复习课的教学中，许多教师都片面地认为要拔高，要增加难度，其实基本知识点和知识框架仍然要给学生厘清，基础不牢，地动山摇.而且在历年的中考中，“三角形全等”经常会出一些中等难度的题目，所以教师在复习时不能走入误区.

2.重视学生终身学习能力的培养

在复习课的备课中，教师首先要明确本节课要落实什么目标，如何组织教学以实现目标的落地有声，选取什么样的例题传递出目标信息.复习课的教学不是教什么知识或回忆什么知识，而是要培养学生的综合素养，教给学生那些能让学生具有终身学习能力的素养.学生的知识梳理、知识迁移、问题洞察、自变问题、自拓问题等，都是落实教学目标的体现，这是复习课教学的最终目的.教师在复习课中引导学生达成目标，是复习课教学的宗旨所在，即培养学生终身学习和终身发展的能力，也就是常说的学科核心素养.

总之，复习课教学尚是一个值得研究的课题，让一节复习课收到事半功倍的效果，我们正在路上！