初中几何折叠问题探究教学的实践与研究

☉江苏省清江中学 张绍俊

折叠问题是中考常考题型，主要考查考生的空间想象能力、动手操作能力、说理计算能力等综合素养.从近几年中考命题看，这类问题着眼点日趋灵活，能力立意逐年加强.因而成为学生应试的痛点与难点.在数学中考复习阶段，探究课应该成为数学复习的常态课.那么，初中几何折叠问题的复习探究课如何上呢？笔者结合教学实践谈谈自己的看法，供大家参考，并提出宝贵意见.

一、几何折叠问题复习探究课的设计

1.引出问题

问题是数学的心脏，复习探究课也不例外.那么，问题来源于何处？笔者认为，问题应来源于课本或最新中考题，应具有典型性.通过典型问题的解决让学生感悟这种题型的特点，感悟这类问题的基本解法.例如：

引题1：（选自新课标人教版数学八年级下学期P126）折纸做30°、60°、15°的角，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平，再次折叠纸片，使点A落在折痕EF上的点N处，并使折痕经过点B得到折痕BM，同时得到线段BN，观察所得到的∠ABM、∠MBN和∠NBC，这三个角有什么关系？

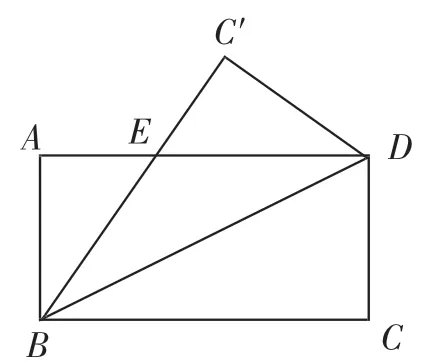
图1

引题2：（2018·四川凉州）如图1，将矩形ABCD沿对角线BD折叠，使点C落在点C′处，BC′交AD于点E，则下列结论不一定成立的是（ ）.

A.AD=BC′

B.∠EBD=∠EDB

通过以上两个问题，引导学生感悟折叠问题的实质就是轴对称的实际应用，对称轴就是折痕所在的直线，折叠前后的图形是重合的，因而它们全等，于是出现了对应边、对应角分别相等.

2.发现问题

上述两个问题，是本节探究课的导火索，后续问题又从哪里来？我认为应来自学生.当然，不是让他们自己编题，而是根据这类问题的特点找题，为了避免他们找题的盲目性，增强合作探究的意识，可以分学习小组合作完成.可以让学生上网查询，也可以让学生查阅资料，进行开放式教学，真正做到开卷有益.

例如，有一组学生经过上网查询，翻阅资料，找到了如下问题：

问题1：如图2，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C与AD边上的点K重合，FH为折痕.已知，则BC的长为_____.

图2

图3

问题2：如图3，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB=___________.

问题3：在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为点E且在AD上，BE交PC于点F.

（2）如图5，①求证：BP=BF；

②当AD=25，且AE＜DE时，求cos∠PCB的值；

③当BP=9时，求BE·EF的值.

图4

图5

3.解决问题

学生发现问题，是探究性复习的第一步，而解决问题才是根本，既然问题是学生提出的，教师应让学生自主完成，让每一个学生小组展示风采，合作完成问题的解决过程.在展示过程中，实现资源共享、共同提高的教学目的.

例如，对于上述三个问题中的问题1，学生在合作探究后，又分工合作如下讲评：

生1：（分析）由题意知∠3=180°-2∠1=45°，∠4=180°-2∠2=30°，BE=KE，KF=FC，作KM⊥BC.设KM=x，可知EM=x，MF=x.根据EF的长求得x=1，再进一步求解可得.

生2：（解答）根据题图与已知条件，∠3=180°-2∠1=45°，∠4=180°-2∠2=30°，BE=KE，KF=FC.如图6，过点K作KM⊥BC于点M，设KM=x，则EM=x，，所以，解得x=1，所以，KF=2，BC=BE+EF+FC=EK+EF+KF=.所以BC的长为

图6

生3：（感悟）解答本题的关键是利用折叠变换的性质，即折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等.同时注意数形结合思想和方程思想的应用，这类几何计算题，往往可以借助列方程来解决，也就是说几何问题代数化.

师：刚才这组同学回答得十分精彩！大家鼓掌！（学生热情鼓掌）他们提供的题目都是以长方形为背景，都是些经典的好题！同学们在解题时请注意以下几点：

第一，折叠问题是一类常见的几何探究性开放题，在三角形、四边形和圆中都可能出现，解决这类问题的根本方法是利用对称轴的性质.我们要根据轴对称的性质去图形中找出折叠前后哪些量发生了变化，哪些量没有发生任何改变，再利用几何知识（如三角形的全等、相似）和代数知识（如函数、方程）建立有关线段、角之间的联系.

第二，折叠图形一定会产生轴对称，就会出现相等的线段和角，为了解题方便，我们通常把它们集中在一起.当题目中含有直角时，我们可将条件集中到较小的直角三角形中，再利用勾股定理求解.

第三，矩形中的折叠问题，往往可依据折叠性质与平行线性质，求出有关角的度数，也可以依据折叠性质和勾股定理，求出线段长度.

第四，当几何图形中出现“折叠”二字时，我们应该马上想到图中一定存在一组全等图形，从而快速找出与题目有关的相等的量.

师：今天的探究课同学们配合得十分默契，体现了互相帮助、共同提高的合作精神.希望大家一如既往地坚持下去！今天的作业，就是请大家选择课上没有交流的3～4个继续探究完成！

（铃声响起，教师宣布下课）

二、关于探究性复习课的几点感想

感想1：探究性复习课的教学模式怎样实施？

中国式教学往往限制在课堂上，而要想让学生真正尝到探究的甜头，必须让他们走出课堂，走向学校的图书馆和电子阅览室，在脱离教师监控后，如何实施？笔者认为，完全可以让学生自己管自己，因为这样做更能体现探究性复习的自主性.当学生查到相关题目后，由学习小组选派代表进行交流，其步骤如下：

第一步：公布本组找到的折叠问题的实例，一般3～4例即可；

第二步：择其中1例进行剖析并解答；

第三步：归纳解题方法和解后反思，允许同组成员适当补充；

第四步：教师加以适当点评，并鼓励学生，让学生获得成就感；

最后，教师要求学生在大家提供的题目中选择3～4个作为本节课的作业.

感想2：探究性复习课中，教师应扮演什么样的角色？

探究性复习课更能体现学生的主体性，教师把探究权完全交给学生，让学生顿生“我的地盘我做主”的感觉，从而激发他们探究的热情，感受探究的成果与乐趣.在这当中，教师不是放任不管，教师不仅要善于放，更要善于收，这就给教师提出了更高的要求，同时更能体现出教师的主导地位.探究内容是由教师定的，教师是组织者，而当学生遇到问题时，教师就是指导者，尤其是对问题认识的高度，离不开教师的悉心指教.教师应信任学生，但不可放任学生.

感想3：中考探究性复习课的适用范围有哪些？

虽然探究性复习课能让学生自由发展，展示个性与才能，但并不是每一节复习课都适宜搞探究性复习，如基础知识的回顾；从另一个角度讲，如果天天如此，学生也会乏味.笔者认为，探究性复习课型以习题课为主，以中考探究性问题为切入点，教师必须精心安排与组织，不可走过场，否则会起到负作用.因为任何事物都有两面性，只有把握恰当，才能让探究性复习课发挥效益.