论数学教学过程中的教与不教
☉四川省成都双流中学实验学校 文传福
数学教学活动需建构在学生的认知基础和知识经验水平之上.教师通过让学生参与数学活动,引导他们通过自主探究、合作交流,理解和掌握数学知识和技能,渗透数学思想方法,从而获取充分的数学活动经验.新课改风向标下,教师在数学课堂教学中,需创设有效的教学情境,提出合理的问题,把控好“教与不教”的尺度,艺术性地处理好“教与不教”的矛盾,激发学生的探究意识,提高学生学习数学的兴趣,让数学学科核心素养在数学课堂上真正得以落实,从而提升教学质量.下面笔者就自身教学中的一些做法和感悟,与同仁交流.
一、教是为了不教
教学过程中,作为课堂教学的组织者和引导者,教师需创设恰如其分、行之有效的教学情境,启发学生多方位、多角度地分析问题、解决问题,充分调动学生的学习积极性,让学生的潜能在最大程度上得以发挥.所谓“教”,就是教师在教学中以启发式引导,激发学生的主观能动性,逐步渗透数学学习方法,激励他们勇于发现、乐于思考、勤于探究,最终实现自主学习.
案例1:学生基本掌握运用直接开方法求解一元二次方程根的问题后,可以引导学生运用配方法求解二次项系数为1的一元二次方程.如果教学过程中,教师直接引入问题“如何求解方程x2-4x-5=0”,学生必定一筹莫展,不知从何下手.笔者创设了以下教学情境,引导学生思考,培养数学思维,启迪学生发现和解决问题:
师:如何解方程(x-2)2=9?
生1:由(x-2)2=9,可得x-2=±3,则x=2±3.则x1=5,x2=-1.
师:很好.能否尝试解方程x2-4x+4=9?
生2:可以看出x2-4x+4=(x-2)2,再将其转化为以上同样形式即可解决.
师:不错.如何解方程x2-4x=5呢?
生3:只需在方程的两边同时加上4即可,即x2-4x+4=5+4.
师:那么如何解方程x2-4x-5=0?
生4:由x2-4x-5=0,得x2-4x=5,则x2-4x+4=5+4,则(x-2)2=9,则x-2=±3,则x=2±3,则x1=5,x2=-1.
师:我们再尝试解方程x2-6x+8=0.
…………
之后笔者引导学生归纳解题方法,如下:
(1)先移动常数项至方程右侧;
(2)再将方程两侧均加上一次项系数一半的平方,使得方程左侧可化为完全平方式;
(3)最后直接用开方法求解.
通过有意识、有计划的引导,激发学生自主发现和探究问题的兴趣,从而促进学生积极、主动思考问题,形成正确解题路径.
案例2:教师出示问题:小红同学通过以下方法求解方程是否正确?请说明原因.
解方程:(x+2)2=4(x+2).
解:方程两边都除以(x+2),可得x+2=4.
则x=2.
大部分学生都认为不正确,原因在于他们认为一元二次方程的解为两个,并非上述解答中的一个.很显然,这是依据表象进行的基本判断.
师:我们可以思考一下,以上解题过程中,问题出在哪一个步骤上呢?
生1:当方程两边同时除以(x+2)时,会出现x+2=0的情况,所以这一步错了.
师:回答得很好.
…………
借助情境的参与,激发学生自主思考和深度探究,让学生在想象、发现、创造的过程中,打开思维空间,感受数学思想方法,提升思维的广阔性和灵活性,培养学生的解题能力,进而提升教学效益.
二、不教也为教
教学中所谓的“不教”,是指对于一些学生可以借助自主思考、探究、合作讨论得出结论的数学问题和数学知识,不需要直接讲授,只需留足时间和空间,引导学生积极思考、自主探究、合作学习,进而解决数学问题.当然,这里所说的不教并不是“完全放养式”,而是恰到好处地教,让学生通过学习数学知识,提升数学素养,创设高效课堂.
案例3:笔者在教完“平方根”后,借助以下教学情境导入“立方根”这一内容:
师:假设我们一起制作一个正方体纸盒,它的容积是27cm3,此纸盒的棱长是多少呢?
生(很快得出答案):3cm.
师:我们再一起制作一个正方体纸盒,它的容积是15cm3,此纸盒的棱长是多少呢?
学生小声讨论,但得不到答案.
师:你们认为这个棱长是否存在?
生:肯定存在.
师:既然一定存在,是多少呢?该如何表示呢?
分析:从以上梯度式情境中引导学生进行对比,感悟出容积为15cm3的正方体纸盒是存在的,进而得出其棱长也是存在的.基于学生的已学知识“平方根”,继续推进教学过程:
师:我们带着这个问题去书本上找寻答案,通过书本内容回答以下几个问题:
①什么是“立方根”?它的意思是什么?
②什么是“开立方”?8的立方根是多少?-125呢?
以上教学设计,一方面,使知识实现正迁移;另一方面,提升学生的阅读理解水平.
案例4:笔者在教学“直角三角形全等的判定”第2课时时,为了引导学生感悟角平分线的性质及判定,提出以下问题:
如图1所示,OC平分∠AOB,OC上有一点P,且PD⊥OA,D为垂足,PE⊥OB,E为垂足,求证:PD=PE.
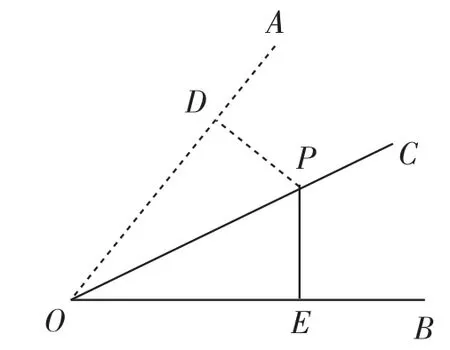
图1
在解题过程中,学生自主观察和思考,而后完整、顺利地写出了解题的过程,并归纳出以下性质:“位于角平分线上的任意一点到角两边的距离都相等.”笔者适时追问:“倘若我们将定理的条件和结论互换,也就是以下命题‘如果有一个点到一个角两边的距离相等,那么这个点一定在这个角的平分线上’,此命题是真命题吗?能否证明?”此刻,学生兴趣盎然,激发了火热的思考、深度的合作探究、思想的碰撞,促进了智慧的生成,证明过程跃然纸上.让笔者最为欣喜的是,整节课中学生自主参与学习过程,可以说深度思考真正实现了,学生的能力自然而然就形成了.
三、教与不教完美统一
在课堂教学中,教师作为学生学习行为的“创设者”,引导学生思考、发问,激发学生深入探究和深度思考.学生既是教学的“客人”,又是教学的“主人”,在学习中引发思考、主动参与、感悟成功,得到发展、促成智慧.所以,学生对教师有一定意义上的依赖性,又具有一定程度上的独立性.课堂教学中,若离开了教师的“教”,学生就无法实现从不会到会,从无知到知,从不行到行,进而实现“不需教”的过程.当然,若离开了学生的“主动学”,主动参与、独立思考、迁移运用所学知识,那么学习则仅仅是浮于表面,毫无深度,教师的“教”也是苍白无力、毫无效果.只有两者完美统一,才能满足学生的求知欲、表现欲和发展欲,提升学生的思维能力,引导学生从数学思想的高度建构知识,进而获得较好的教学效果.
多年的教学与实践显示,教学中需做到“有所教,有所不教”,将教与不教完美统一,才能消除教学中的机械重复,使教学过程生动、有趣,使学生由“学会”走向“会学”,充分调动学习的兴趣,学会学习方法,培养学生自主学习的能力,从而实现终身享用.当然,对于学生自主学习能力的发展而言,教师还有很长的路要走,需要做到钻研教材和探究学生的具体学情,并基于教材和具体学情,创设行之有效的教学情境,促进学生思维的发展.当然,有效的教学情境创设仅仅是其中的一个环节,掌握好“教与不教”的艺术才是关键,使数学课堂尽可能鲜活、生动,全面激活学生的思维,让学生在自主、合作、探究的过程中,感悟数学知识,积累数学技能,促进数学学科核心素养的提升.

