小题需大做，“滚”动出精彩*——一节综合与实践活动课的教学实录与思考

☉江苏省南京市雨花台中学 梁海波

一次九年级测验后，学生对一道选择题的答案争议较大并展开了热烈的讨论.笔者结合学生的讨论和思考，设计并上了一节综合与实践活动课“滚动的圆”，在公开课展示活动中受到广泛好评.本文把课堂教学实录整理如下，并将笔者的教学思考整理成文，以期与各位同行研讨交流.

一、教学实录

1.开门见山，抓住知识生长点

问题1：（原题改）将两枚同样大小的硬币放在桌上，固定其中一枚，另一枚则沿着其边缘滚动1圈，此时滚动的硬币滚动了几圈？

生1：1圈，两枚同样大小的硬币说明这两枚硬币的周长是相等的，所以一枚硬币沿着另一枚滚动1周，刚好就滚动了1个周长，也就是1圈.

师：有不同的答案吗？

（大部分学生沉默，几名学生站起来说“不对”，但讲不清问题在哪儿）

师：既然通过思考无法确定结果，我们可以动手操作体验一下.

学生活动：小组合作实验，用瓶盖模仿硬币的滚动，动手操作验证猜想，提醒学生注意滚动的过程中不要出现滑动.

（学生操作，教师提醒学生操作要规范）

师：大家都完成了实验，实验的结果是什么呢？

（多数学生说2圈，少数学生说1圈）

师：下面请一名同学来操作演示.

（生2实物投影展示，结果是2圈）

师：有没有同学知道为什么呢？

（学生沉默）

师：本节课我们带着这个问题来探究滚动的圆，刚才的操作中大家已经初步体会了图形的滚动，但在圆上滚动的情形比较复杂，我们如何去研究一个复杂问题呢？

生：从简单入手.

师：圆在什么图形上运动比较简单？

生：在直线上.

师：下面我们就从圆在直线上的滚动开始研究.

设计意图：利用生活中的数学问题，创设有效的问题情境，让学生的思维受到适度挑战，激发学生的学习兴趣.同时，通过回顾学生已有的知识和经验，回归解决问题的本质，将复杂的问题简单化，从简单、特殊的问题开始探究.

2.化“疑”为简，寻找问题突破口

问题2：如图1，将一个半径为r的圆在直线上滚动1圈，则这个圆滚过的路径长为？思考图2中哪条线段长是圆滚过的路径长.（动画展示滚动过程）

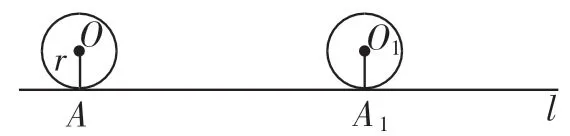
图1

生3：路径长为2πr，线段AA1的长就是圆滚过的路径长.

追问1：在圆滚动的过程中，什么没有变？什么发生了改变？

生4：圆的大小和形状都没有改变，圆的位置发生了改变.

生5：圆与直线的位置关系也没有改变，始终是相切.

追问2：圆心所经过的路径是什么图形？

（动画展示滚动过程，如图2）

图2

生6：一条线段，圆心到直线的距离没有改变，始终等于半径.

追问3：这条线段多长？你有何发现？

生6：是2πr，我发现圆心经过的路径长等于圆滚过的路径长.因为圆O始终与直线l相切，所以OA和O1A1都与直线l垂直，那么OA平行且等于O1A1，则四边形OAA1O1是矩形，即OO1等于AA1.所以圆心经过的路径长等于圆滚过的路径长.

问题3：若线段AB=4πr，则此半径为r的圆从点A无滑动地滚动到点B需转几圈？

生7：2圈，用4πr除以2πr得2.

师：当圆在直线上滚动时，圆滚动的圈数应该怎么求？

生8：圆滚动的圈数等于圆滚过的路径长除以圆周长，即等于圆心经过的路径长除以圆周长.

设计意图：回归学生思维的最近发展区，探究圆在直线上滚动的过程，在变化中寻求不变.在操作中搭建学生思维的桥梁，寻求主线问题的突破口，体会直线上圆的滚动过程即平移与旋转的复合运动.

3.拾级而上，操作中探究方法

图3

问题4：如图3，将总长为4πr的线段AB在中点C处折成90°，此时这个半径为r的圆从点A到点B需滚动几圈？

生9：还是2圈，因为线段长度还是4πr.

追问1：有不同意见吗？

生10：我认为不是2圈，感觉比2圈多一点.

追问2：为什么会多一点？

生10：在折点C处，圆多转了一些.

师：请大家动手操作并思考能否得到滚动的具体圈数.

（学生动手操作）

（学生自发鼓掌）

师：精彩！一起看滚动的过程！（动画展示滚动过程，如图4）

追问3：有其他思路吗？可以从圆心经过的路径来解释吗？

生12：可以的，圆心经过的路径是两条线段加一条圆弧，两条线段的长度一共是4πr，圆弧的半径为r，圆心角为90°，弧长是，所以圆心经过的路径长是.然后用圆心经过的路径长除以圆周长，也可以得出圈.

师：这名同学的回答很精彩，说明这个问题既可以用角度去解决，又可以用圆心经过的路径来解决.（学生自发鼓掌）

图5

问题5：如图5，将总长为4πr的线段AB在中点C处折成60°，此时这个半径为r的圆从点A到点B需滚动几圈？

师：还有其他思路吗？

设计意图：探究圆在折线上滚动的过程，在操作中感受折点处圆的运动，体会在折点处即圆的自转与公转的复合运动，以圆公转的角度和圆心运动的路径刻画运动过程，由表及里，逐步发现解决问题的关键.

4.破解难点，极限思想转化核心问题

图6

问题6：如图6，连接AB，此时这个半径为r的圆沿△ABC的外侧滚动1周需滚动几圈？

师：你能分别从旋转的角度和圆心运动的路径来解释吗？

生15：圆在三角形三个顶点处做旋转运动，加起来一共旋转了360°，所以转了1圈.圆心在三个顶点处的运动路径合起来恰好是1个圆周，所以通过圆心经过路径除以圆周长也是1圈.最终的答案是3圈加1圈，即4圈.

师：精彩！如果将特殊的三角形变为特殊的四边形呢？

问题7：如图7，将等边三角形改为正方形，则这个圆沿正方形的外侧滚动1周需滚动几圈？

（学生略加思考后齐答：5圈）

师：继续增加难度，如果将特殊的图形换成一般的多边形，结论还成立吗？

图7

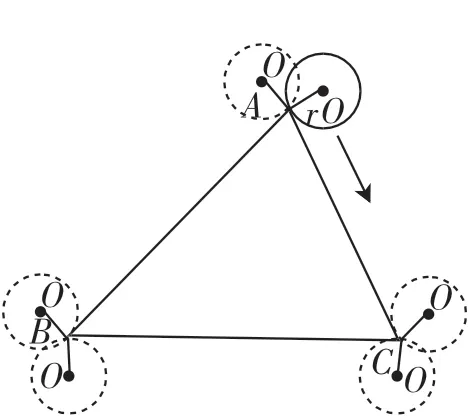
图8

问题8：如图8，将等边三角形改为任意三角形，且该三角形的周长为a，则这个半径为r的圆沿△ABC的外侧滚动1周需滚动几圈？独立思考后小组讨论.

（两分钟后，陆续有学生举手）

师：为什么圆在三角形顶点处滚动的角度和为360°？

生16：顶点处滚动的角度与每个内角是互补关系，数值上等于外角，三角形的外角和是360°，所以圆在几个顶点处滚动的角度之和为360°.

师：如果继续将四边形改为任意的多边形呢？

师：你能否归纳出圆在多边形的外侧滚动的圈数如何计算？生16：圆滚动的圈数=+1.

师：你回答得很好，下面大家来一起回顾我们的探究过程.

问题9：若多边形的周长为2π，滚动1周需滚动几圈？

生：（齐）2圈.

师：如图9，如果无限增加多边形的边数，此时多边形将会接近于一个圆，让半径为r的圆沿着该圆外侧滚动1周，滚动几圈呢？

生：（齐）2圈.

图9

设计意图：层层递进，探究圆在封闭的多边形上滚动的过程，在操作中感知圆滚动的过程中变与不变的元素.在探究中发现问题的本质，从特殊到一般，在不断增加边数的过程中体会极限的数学思想.

5.回归主线，交流中探寻原理

图10

师：回到开始的问题，现在你能结合本节课所探究的经验，解释为什么硬币滚动的是2圈吗？

（动画展示滚动过程，如图10）

生：从旋转角度来看，滚动的硬币滚动了1个圆周长，同时也旋转了1个圆周360°，所以是2圈.

生：从圆心经过的路径长来看，圆心的路径是一个半径为2r的圆，路径长为2π乘以2r等于4πr，用圆心经过的路径长除以圆周长，即4πr除以2πr，结果为2圈.

设计意图：回归探究圆在圆周（曲线）上滚动的过程，首尾呼应，突破本节课的难点，在一系列问题的解决和探究中，让学生感悟数学探究的魅力.

6.课堂小结，提炼核心思想

师：回顾解决问题的过程，你学到了哪些知识？有什么收获？

生：研究圆的滚动，可以从两个方向去探究，一个是圆在滚动过程中旋转的角度，另一个是圆心经过的路径长.

生：探究问题可以先易后难，从简单出发，逐步深入探究复杂问题.

设计意图：通过小结，梳理探究思想，总结探究活动中获得的经验，提炼核心思想，同时锻炼学生的语言表达能力，培养学生勇于发表自己见解的能力.

二、教学思考

1.激发兴趣，探究中积累活动经验

《义务教育数学课程标准（2011年版）》（以下简称《标准》）中明确提出，教师教学应该以学生的认知发展水平和已有的经验为基础，面向全体学生，注重启发式和因材施教.教师要发挥主导作用，处理好讲授与学生自主学习的关系，引导学生独立思考、主动探索、合作交流，获得基本的数学活动经验.

为了激发学生的学习兴趣，教师需要悉心准备和策划合理的教学过程，设计的教学活动应以学生的数学认知规律为基础，给学生提供更广阔的探究空间.以本节课为例，教师以硬币滚动的问题设计引入，学生提出猜想，发现操作结果与猜想不一致，激发了进一步探究的兴趣.教师引导学生发现硬币滚动问题本质上是圆的滚动，接着让学生思考如何去探究这一问题.学生从圆在直线上的滚动开始，延伸到折线上的滚动，再到特殊多边形乃至任意多边形上的滚动，最终回归到圆的滚动上，遵循了从特殊到一般的研究思路.

2.着力基础，探究中把握知识生长

综合与实践活动课需要以学生课内知识为基础进行生长.笔者认为基础的知识点有两处：一处是图形的运动，学生对于图形三种基本的运动方式已经非常熟悉，但是对于复合的运动方式尚且生疏；另一处是圆的相关知识，特别是点与圆的位置关系及直线与圆的位置关系等，为本节课的探究提供了有效的知识铺垫.

课堂教学中，教师宜从这两处入手.（1）从基本的图形运动方式进行知识生长，可看作平移和旋转的复合运动.当圆在直线上滚动时，可以看作“整体平移与局部旋转的复合”，从整体看是整体的平移，从局部看是圆自身的旋转；当圆在折线上滚动时，直线部分与前一种情形是一致的，学生探究的难点在于圆在折点处的运动.（2）从复合运动的角度进行知识生长，折点处圆的滚动可以看作“整体旋转与局部旋转的复合”，即折点处圆整体绕着折点做旋转运动，同时自身也在转动.同样，圆在多边形和曲线上的滚动都可以看作平移与旋转的复合运动.

值得注意的是，教师在课堂上的关键环节需要放慢节奏，给予学生充分的操作和思考时间，学生探究的过程即是知识不断联系、重塑和发展的过程，更是知识生长的过程，教师要帮助学生把握好这一过程.

3.立足实践，探究中提升数学素养

《标准》中还明确指出，数学是人类文化的重要组成部分，数学素养是现代社会每一个公民应该具备的基本素养.数学综合与实践活动的教学本质是思维的教学，综合与实践活动课应以操作和实验作为基础，引领学生的思维，通过课堂上的操作活动启迪学生的思考.

课堂上教师不仅要关注学生掌握解决问题的方法，更要关注学生数学素养的提升.在本节课中，学生从具体的硬币滚动中抽象出基本图形即圆的滚动，积累了从具体到抽象的活动经验，发展了学生数学抽象的能力.同时，学生从已有的知识和经验出发，有目的地探索圆在不同图形上滚动的过程，在不断深入的探究和思考中，学生进一步发展了几何直观和空间想象的能力.整节课，通过师生间的共同探究，让学生经历知识的发生过程，从而获得数学活动经验，进而让综合与实践活动成为提升学生数学学科核心素养的载体.