张量E-特征值包含集及其应用

桑彩丽, 赵建兴

(贵州民族大学 数据科学与信息工程学院, 贵州 贵阳 550025)

1 预备知识

设n为正整数,n≥2,令N={1,2,…,n}.用C(R)表示复(实)数域.设A=(ai1i2…im),若

ai1i2…im∈R,ij∈N,j=1,2,…,m,

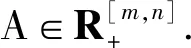
ai1i2…im=aπ(i1i2…im),

则称A为对称张量.

若齐次多项式

满足▽Axm=mAxm-1,则称A为弱对称张量[1].由文献[1]知,当m=2时,对称张量和弱对称张量是一样的.当m≥3时,对称张量是弱对称张量,反之,不一定成立.

若存在数λ∈C和向量x=(x1,x2…,xn)T∈Cn{0}满足

Axm-1=λx,xTx=1,

则称λ为A的E-特征值,x为相应于λ的E-特征向量,其中Axm-1为n维向量,其第i个分量为

用σE(A)表示A的所有E-特征值作成的集合.若λ和x均为实数,则称λ为A的Z-特征值,x为相应于λ的Z-特征向量[2-3].用σZ(A)表示A的所有Z-特征值作成的集合,称

(A)=max{|λ|:λ∈σZ(A)}

为A的Z-谱半径[1].

由于张量的Z-特征值及其Z-特征向量与统计数据分析中的最佳秩一逼近联系密切[4],引起了广泛关注[5-17].最近,许多专家学者对张量A的Z-特征值进行了定位[10-14],其中文献[10]给出了A的Geršgorin-型Z-特征值包含集和Z-谱半径的一个上界.

定理 1.1[10]设A∈R[m,n],则

其中

Ki(A)={z∈C:|z|≤Ri(A)},

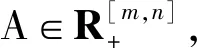
为了对Z-特征值进行更精确的定位,文献[10]获得了如下Brauer-型Z-特征值包含集.

定理 1.3[10]设A∈R[m,n],有

其中

Ni,j(A)={z∈C:(|z|-(Ri(A)-

进一步,N(A)⊆K(A).

由定理1.3中Z-特征值包含集,文献[10]获得Z-谱半径的如下更精确的上界.

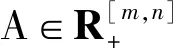
本文在定理1.1和定理1.2的基础上考虑张量A的E-特征值定位问题,首先将定理1.1和定理1.3中的Z-特征值包含集推广到E-特征值包含集.其次,利用不等式放缩技巧给出张量A的更精确的E-特征值包含集.最后,作为应用,给出弱对称非负张量Z-谱半径的更精确的上界,改进了定理1.2和定理1.4中的结果.

2 主要结果

应用类似于文献[10]中定理3.1和定理3.4的证明,易将定理1.1和定理1.3中的Z-特征值包含集推广到如下E-特征值包含集.

定理 2.1设A∈R[m,n],则σE(A)⊆K(A)且σE(A)⊆N(A).

下面给出比定理2.1中包含集K(A)和N(A)更精确的E-特征值包含集.

定理 2.2设A∈R[m,n],则

其中

证明设λ为A的任意E-特征值,其对应的E-特征向量为x=(x1,…,xn)T∈Cn{0},即

Axm-1=λx且xTx=1.

(1)

令|xt|≥|xs|≥max{|xi|:i∈N,i≠t,s},显然,0<|xt|m-1≤|xt|≤1.由(1)式的第t个方程

得

|λ||xt|m-1≤|λ||xt|≤

即

(2)

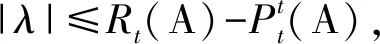
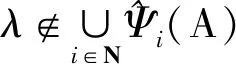
得

|λ||xs|m-1≤|λ||xs|≤

即

(3)

由(2)和(3)式相乘，并消去|xt|m-1|xs|m-1>0得

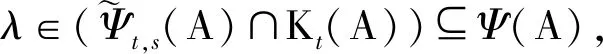
下面对定理2.1和定理2.2中的E-特征值包含集进行比较.在此之前,先引入一个引理.

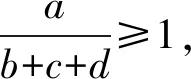
定理 2.3设A∈R[m,n],则定理2.2中的E-特征值包含集比定理2.1中的E-特征值包含集精确,即

Ψ(A)⊆N(A)⊆K(A).

下面分2种情形证明.

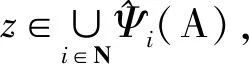
此时对任意j∈N,j≠i0,有

因此z∈Ni0,j⊆N(A).

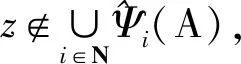
(4)

此时

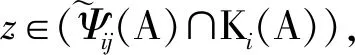
|z|≤Ri(A),

(5)

且

(6)

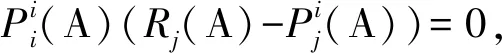
(7)

由(5)和(7)式相乘得

此时z∈Nji(A)⊆N(A).

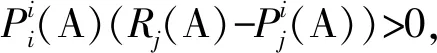
(8)

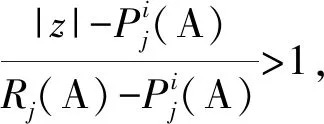
再由(8)式得

由此得

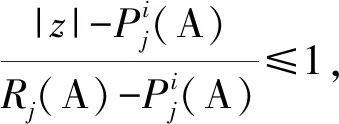
此时z∈Nji(A)⊆N(A).

综合情形1和情形2可知结论Ψ(A)⊆N(A)成立.证毕.

下面应用定理2.2中的E-特征值包含集给出弱对称非负张量Z-谱半径的一个新上界.

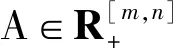
(A)≤Ψmax=

其中

证明由文献[10]中引理4.4知(A)是A的Z-特征值，因此由定理2.2知

(A)∈Ψ(A)=

(9)

((A)-

由(10)式得

因此

(11)

由(9)和(11)式可知结论成立.

由定理2.3易得如下比较定理：

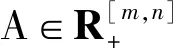
3 数值算例

例 3.1设A=(aijk)∈R[3,3],其中

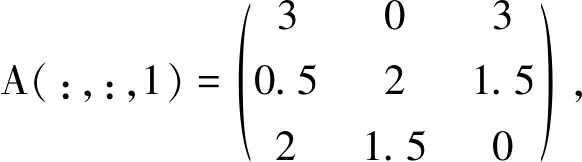
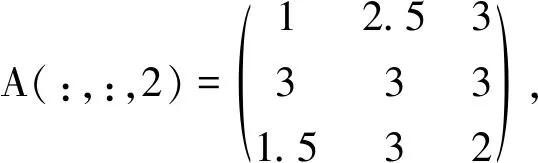
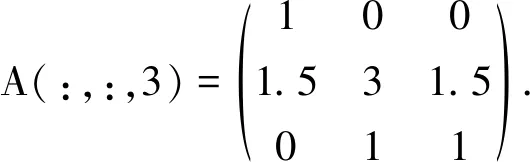
易知A是弱对称非负张量.经计算,得A的所有E-特征值±9.102 6,±2.997 8±0.260 0i,±1.779 3,±1.573 7,±0.889 5,±0.153 2和Z-谱半径(A)=9.102 6.

1) 首先下面对A的所有E-特征值进行定位.由定理2.1得

K(A)={z∈C:|z|≤19}

和

N(A)={z∈C:|z|≤17.793 5}.

由定理2.2得

Ψ(A)={z∈C:|z|≤17.189 5}.

张量A的E-特征值包含集K(A)、N(A)、Ψ(A)和所有E-特征值(见图1),其中K(A)、N(A)和Ψ(A)分别为外侧实边界、中间虚边界和内侧实边界标出,所有E-特征值用“+”号标出.由图1可以看出

σE(A)⊆Ψ(A)⊂N(A)⊂K(A).

2) 其次,对A的Z-谱半径(A)进行估计.由文献[5-13]中相应定理得到的数值结果见表1.

表 1 (A)的下界

Tab. 1 The nether of (A)

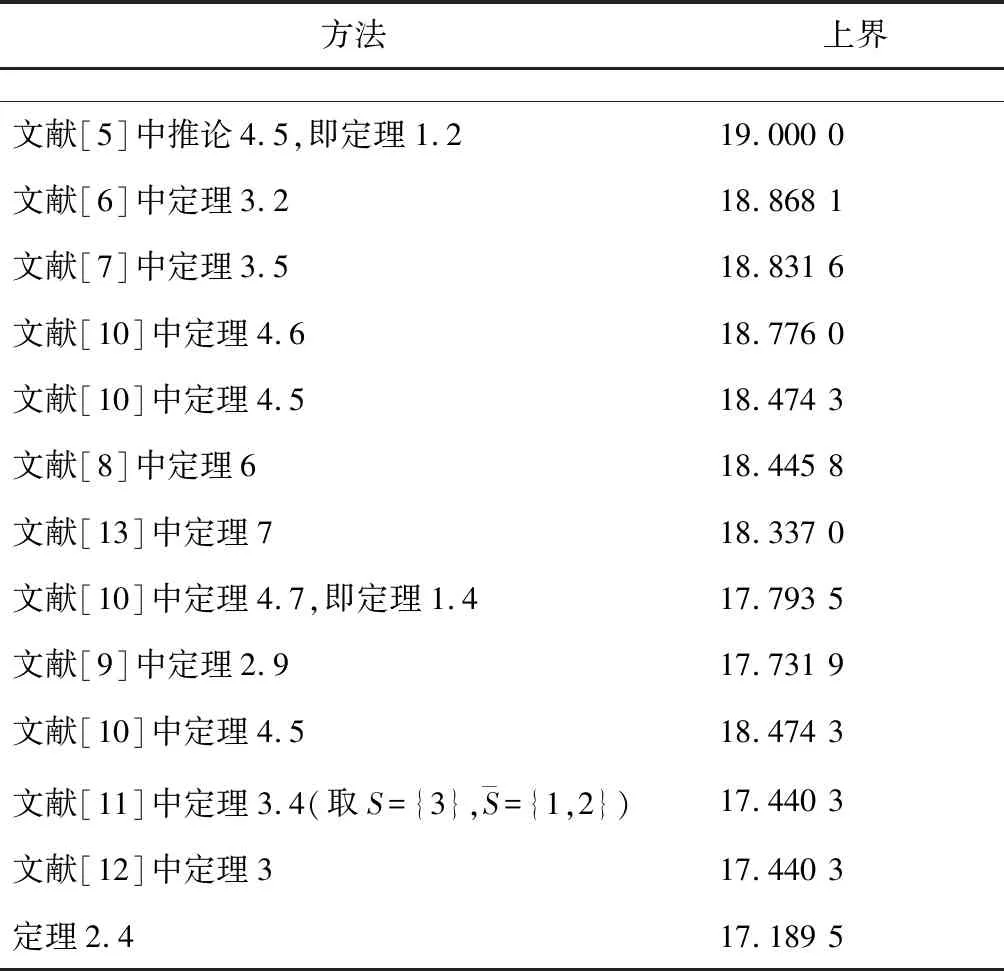
表 1 (A)的下界

方法上界文献[5]中推论4.5,即定理1.219.000 0文献[6]中定理3.218.868 1文献[7]中定理3.518.831 6文献[10]中定理4.618.776 0文献[10]中定理4.518.474 3文献[8]中定理618.445 8文献[13]中定理718.337 0文献[10]中定理4.7,即定理1.417.793 5文献[9]中定理2.917.731 9文献[10]中定理4.518.474 3文献[11]中定理3.4(取S={3},S={1,2})17.440 3文献[12]中定理317.440 3定理2.417.189 5

例 3.2设A=(aijkl)∈R[4,2]为对称张量,其中a1111=7,a1112=3,a1122=2,a1222=3,a2222=7.经计算,得A的所有E-特征值0.5、12.5、25和Z-谱半径(A)=12.5.下面对A的所有E-特征值和Z-谱半径(A)进行定位或估计.由定理2.2得

Ψ(A)={z∈C:|z|≤25}.

由定理2.4得

(A)≤25.

张量A的所有E-特征值及其包含集Ψ(A)见图2,其中Ψ(A)用实边界标出,所有E-特征值用“+”号标出.由图2可以看出，σE(A)⊆Ψ(A)且Ψ(A)恰好包含了A的所有E-特征值.

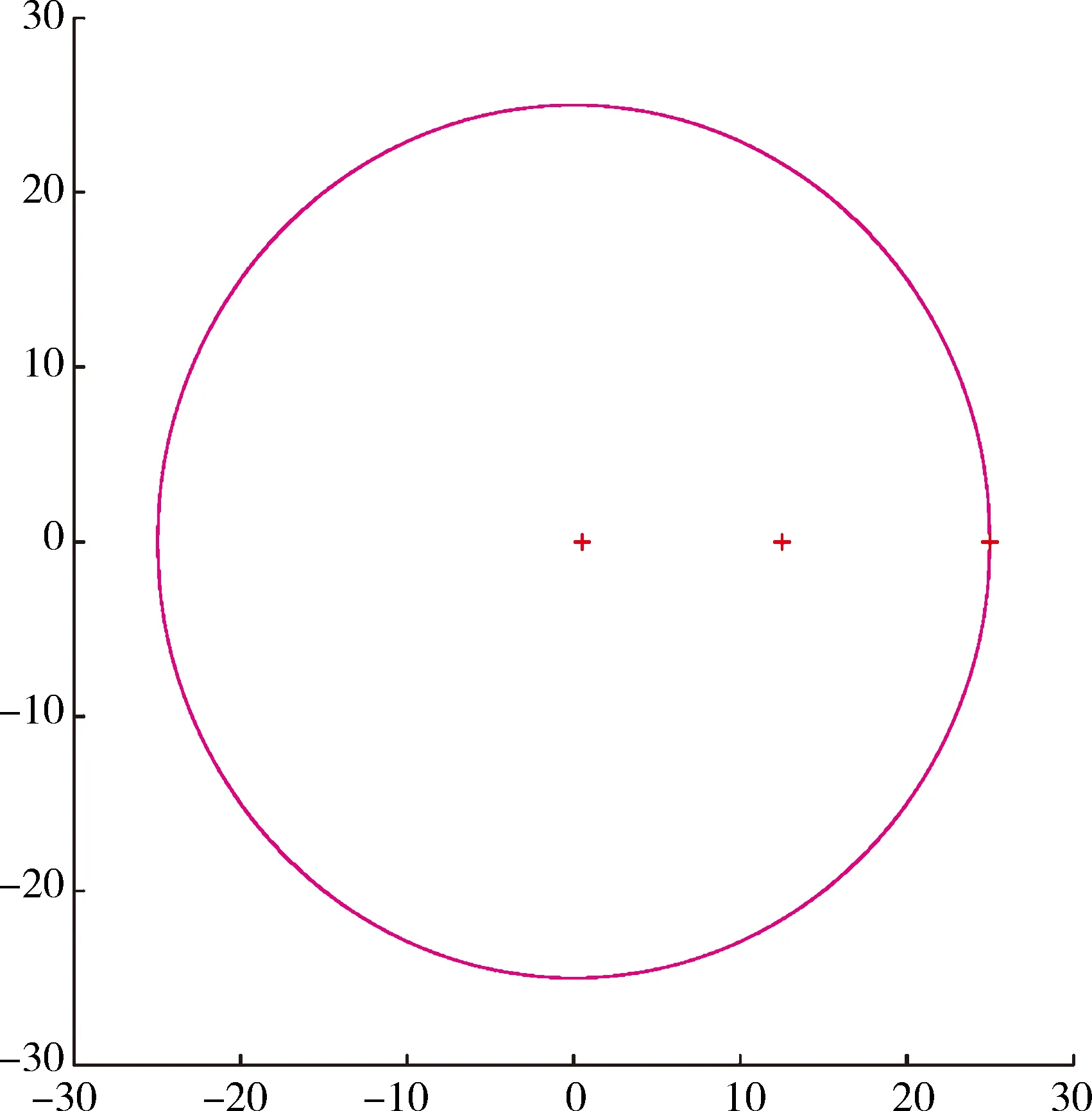
图 2 张量A的E-特征值及其包含集Ψ(A)