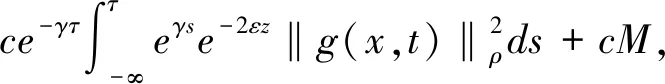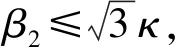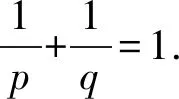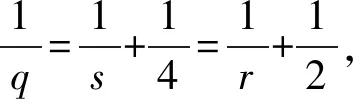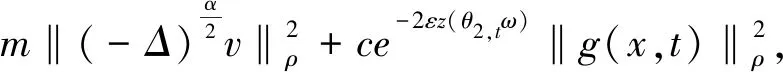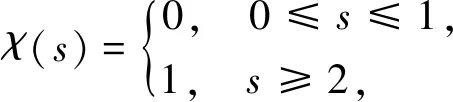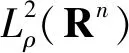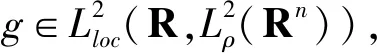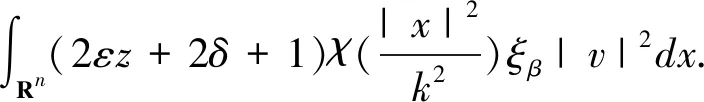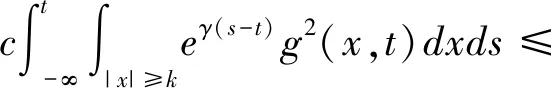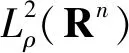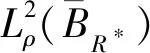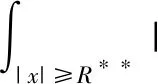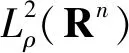加权空间中带乘性噪声的随机分数阶非自治Ginzburg-Landau方程
王云肖, 舒 级, 杨 袁, 李 倩, 汪春江
(四川师范大学 数学科学学院, 四川 成都 610066)
1 引言及预备知识
近年来,在物理、生物、化学等领域关于分数阶偏微分方程已被广泛研究与应用,例如分数阶Schrödinger方程[1-3]、分数阶Landau-Lifshitz方程、分数阶Landau-Lifshitz-Maxwell方程和分数阶Ginzburg-Landau方程[4-7].
分数阶Ginzburg-Landau方程能在分形色散的介质中描述动力过程.文献[8-12]讨论了关于确定性的Ginzburg-Landau方程,并讨论了其长时间行为以及分数阶Ginzburg-Landau方程的适定性和动力学行为.对于随机分数阶Ginzburg-Landau方程,文献[13-18]讨论了其渐近动力学和随机吸引子的存在性.无界区域中以及非自治的情况在文献[19-21]中有所介绍.由于L2和L2×L2空间具有平移不变性,得到的解不包含行波解,从而就遗漏了一些解.因此,选取更大的相空间使其包含行波解等其他重要的解,同时又要保证吸引子的存在性,其中一个难点就是得到解的渐近紧性,渐近紧性可以用来得到紧吸收集的存在性.因此,需要在加权空间中讨论其随机吸引子[22-23].
本文考虑如下加权空间中带乘性噪声的随机分数阶非自治Ginzburg-Landau方程
du=[-(λ+iβ1)(-Δ)αu-
(κ+iβ2)|u|2σu+δu+g(x,t)]dt+
uεh(x)dW(t),x∈Rn,t>τ,
(1)
具有初始条件
u(x,τ)=uτ(x),x∈Rn,
t>τ,τ∈R,
(2)
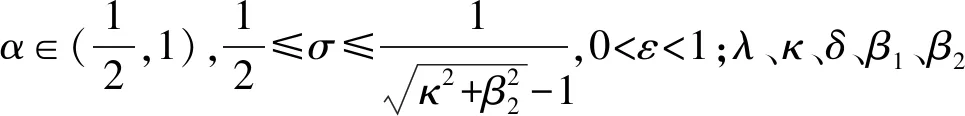
首先给出随机动力系统的一些相关知识.若(Ω,F,P)是一个概率空间,{θ:Ω→Ω},t∈R+是一簇保测度变换,并且映射(t,ω)|→θtω是可测的,θ0=IX,θt+s=θt·θs,其中,s,t∈R,则(θt)t∈T是一个流,((Ω,F,P),(θt)t∈T)是一个可测动力系.
定义 1[14]设(X,d)是可分的距离空间,F是Borelσ-代数,θt是(Ω,F,P)对应的保测度变换,若可测映射
在X上满足:
1)S(0,ω)=IX;
2) 对任意的s,t∈R,ω∈Ω,有
S(t+s,ω)=S(t,θsω)∘S(s,ω),
其中∘ 代表复合算子;
3)S(t,ω):X→X是连续的;
那么称S是一个连续随机动力系统.
定义 2[14]给定一个随机集K,集合
称为K的Ω-极限集.
定义 3[17]若S是随机动力系统,存在随机紧集ω|→A(ω)满足以下条件:
1)A(ω)是严格不变的,即对于所有t>0,S(t,ω)A(ω)=A(θtω);
2)A(ω)吸引所有确定有界集B⊂X;
那么称A(ω)为S的随机吸引子.
定理 1[18]假设S是Polish空间上的随机动力系统,若存在紧集ω|→K(ω)吸收每一有界非随机集B∈X,那么集合
是S的随机吸引子.
接下来给出交换子估计的相关引理[15].
引理 1设u∈Lq,并且对于u的m阶导数为Dmu∈Lr,1≤q,r≤∞.对于Dju,0≤j 并有 引理 2假设S>0,并且p,p2,p3∈(1,∞).如果f,g∈S,并且 则有 ‖f‖Hs,p3‖g‖p4), C(‖▽f‖p1‖g‖Hs-1,p2+‖f‖Hs,p3‖g‖p4). 下面给出分数阶拉普拉斯算子和分数阶Sobolev空间[23]. 令H2α(Rn)表示在标准α下这个完备Sobolev空间 根据定义(-Δ)α,有引理3. 引理 3若f,g∈H2α(Rn),则 其中α1和α2是非负的且α1+α2=α. 给出在加权空间中对于随机分数阶非自治Ginzburg-Landau方程生成一个连续的随机动力系统.研究问题(1)和(2)的解在加权Sobolev空间下的一个加权函数 ξ(x)=(1+|x|2)-b,x∈Rn 其中{u:Rn→R}有界,且 且 ξβ(x)=(1+|βx|2)-b,x∈Rn, 且 规定t∈R,在R上定义一个转化θ1,t为 θ1,t=τ+t,τ∈R, 表示为 Ω=ω∈C(R,R):ω(0)=0. 接下来,考虑概率空间(Ω,F,P),F是由Ω中产生的Borelσ-代数,P是在(Ω,F)上对应的Wiener测度,同时对于时间变换定义为 θ2,tω(·)=ω(·+t)-ω(t),ω∈Ω,t∈R, 则(Ω,F,P,(θ2,t)t∈R)是度量动力系统. 接下来,讨论带有乘性噪声的随机分数阶非自治Ginzburg-Landau方程可以生成一个连续的随机动力系统.由于带有乘法噪声的非自治随机分数阶非自治Ginzburg-Landau方程可以简化为带有可以根据合适变化的随机参数的方程,则有 且有随机偏微分方程: dy+ydt=dW(t), z(θ2,tω)=h(x)y(θ2,tω), e2σεz(θ2,tω)≤r(ω), (3) 其中在P-a.e.ω∈Ω下r(ω)满足 (4) 因此,对于P-a.e.ω∈Ω有 (5) 令 v(t,τ,ω,v0)=u(t,τ,ω,u0)e-εz(θtω), 其中u(t,τ,ω,u0)是问题(1)和(2)的解,v(t,τ,ω,v0)满足 (κ+iβ2)e2σεz(θ2,tω)|v|2σv+δv+ g(x,t)e-εz(θ2,tω)+εz(θ2,tω)v, (6) 初值条件 v0=u0e-εz(θ2,tω),x∈Rn, 且 γ<0. φ(t,τ,ω,u0)=v(t,τ,ω,v0)= u(t,τ,ω,u0)e-εz(θ2,tω). φ(t,τ,ω,v0)=u(t,τ,ω,u0), 值得注意的是,这2个随机动力系统φ和φ是等价的.若φ有一随机吸引子,容易证得φ也有一随机吸引子.因此,仅仅需要考虑随机动力系统φ. 在此,对当τ 引理 4对于任何τ∈R,ω∈Ω,存在T(τ,ω,B)≥0,使得v(t,τ,ω,v0)满足 t≥T(τ,ω,B), t≥T(τ,ω,B). 证明(6)式与ξβv作内积且取实部,有 (7) 首先,估计(7)式等号右边第二项,有 (8) 对于第一项和第三项,有 (9) (10) 根据(8)~(10)式,有 (11) (11)式两边同时乘eγt且在(τ-t,τ),t∈R+上积分,有 (12) 将ω替换为θ2,-τω,有 v(s,τ-t,θ2,-τω,vτ-t)|2dxds≤ 则存在T=T(τ,ω,D)≥0,vτ-t∈D(τ-t,θ2,-tω)且D具有缓增性,有 e-γt‖vτ-t‖2≤1,t≥T, t≥T(τ,ω,B). 通过以上不等式,有 t≥T(τ,ω,B). 证毕. 引理 5对于任何τ∈R,ω∈Ω,存在T(τ,ω,B)≥0,则解v(t,τ,ω,v0)满足 t≥T(τ,ω,B). 证明注意到eγs≥eγ(1-τ)对于所有s∈(τ-1,τ).因此,通过(13)式有 引理 6对任何τ∈R,ω∈Ω,存在T(τ,ω,B)≥0,则解v(t,τ,ω,v0)满足 t≥T(τ,ω,B). 证明(6)式与ξ(-Δ)αv作内积且取实部,有 e2σεz(θ2,tθ-τω)|v|2σv(-Δ)αvdx+ (14) 首先,估计(14)式等号右边第三项,有 (15) |v|2σv(-Δ)αvdx|= (16) 有 m=2(δ+εz(θ2,tω)+ 令t≥0,t∈R,ω∈Ω.对(17)式在s∈[τ-1,τ]下进行积分,得到 (18) 将ω替换为θ2,-τω,得到 因此 证毕. 引理 7对任何τ∈R,ω∈Ω,存在T(τ,ω,B)≥0,则解v(t,τ,ω,v0)满足 证明有 m=2(δ+εz(θ2,tω)+ 令t≥τ,t∈R,ω∈Ω.对(17)式在s∈[τ-t,τ]下进行积分,得到 且 因此 引理 8对任何τ∈R,ω∈Ω,存在T(τ,ω,B)≥0,则解v(t,τ,ω,v0)满足 t≥T(τ,ω,B). 证明通过引理7,将τ替换为t且t≥T1,有 引理 9对任何τ∈R,ω∈Ω,存在 且 R*=R*(τ,ω,ε)>0, |v(τ,τ-t,θ2,-τω,vτ-t(θ-τω))|2dx≤η. 证明假设一光滑函数χ,对任何s≥0,使得0≤χ(s)≤1,有 (19) 首先,估计(19)式等号右边第一项,有 (20) (21) 通过以上不等式有 通过引理4和引理6,存在T1=T1(B,ω)>0使得对所有t≥T1,有 (23) (22)式两边同乘eγt,在(T1,t)上积分,使得对所有t≥T1有 (24) 将(24)式中ω替换为θ2,-τω,对所有t≥T1有 (25) 接下来,将对(25)式等号右边的每项进行估计.对第一项,将τ替换为T1且对引理4中将ω替换为θ2,-τω,有 (26) 因此,存在T2=T2(B,ω,ε)>T1使得对所有t≥T2,有 通过引理1,存在T3=T3(B,ω)>T1,将τ替换为t,对(25)式等号右边第二项,有 且 通过引理8,存在T4=T4(B,ω)>T1,对(25)式等号右边第四项,有 将s替换为t,得 对所有t≥T5和k≥R2,有 令 T*=T*(B,ω,ε)=max{T1,T2,T3,T4,T5}. 通过以上不等式,对所有t≥T*,k≥R*=max{R1,R2},有 这意味着对所有t≥T*和k≥R*,有 证毕. 接下来,证明在无界区域Rn中,由问题(6)生成的随机动力系统的随机吸引子的存在性.通过引理4,则D中φ有闭的随机吸收集.φ的D-拉回渐近紧被证明,其中会运用到尾估计. φ(τn,tn,θ2,τn-tnω,vτ-t,n(θτn-tnω)) B={B(ω)}∈D, 且 v0,n(θτn-tnω)∈B(θτn-tnω), 其中tn→∞. 证明令τn,tn→∞,B={B(ω)}∈D且 v0,n(θ2,τn-tnω)∈B(θ2,τn-tnω). 根据引理4,ω∈Ω时, φ(τn,tn,θ2,τn-tnω,v0,n(θ2,τn-tnω))→ 根据引理4和引理8,存在 T1B=T0B(ω)+1 使得对所有t≥T1B, (29) 令N2=N2(B,ω)充分大,当n≥N2时有tn≥T1B.根据(29)式,对所有n≥N2,有 (30) 令 通过嵌入 的紧实性,同(30)式,根据R*到子序列, φ(τn,tn,θ2,τn-tnω,vτ-t,n(θ2,τn-tnω))→, N3=N3(B,ω) 对所有n≥N3有 ‖φ(τn,tn,θ2,τn-tnω,vτ-t,n(θ2,τn-tnω))- (31) R**=R**(ω)>0, 使得 (32) 令R′=max{R*,R**}和N′=max{N1,N3},则根据(28)~(30)式,对所有n≥N′, ‖φ(τn,tn,θ2,τn-tnω,vτ-t,n(θ2,τn-tnω))- ‖φ(τn,tn,θ2,τn-tnω,vτ-t,n(θ2,τn-tnω))- 由此可知 φ(τn,tn,θ2,τn-tnω,vτ-t,n(θ2,τn-tnω))→ 根据定理1得:
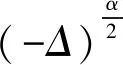
2 随机分数阶非自治Ginzburg-Landau方程的解及其对应的随机动力系统
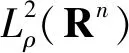

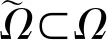
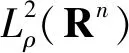
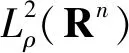
3 解的一致估计以及随机吸引子的存在