一类具有无穷时滞Lotka-Volterra模型的鲁棒稳定性和部分变元鲁棒稳定性

钟玲莉, 李树勇

(1. 四川师范大学 数学科学学院, 四川 成都 610066； 2. 绵阳师范学院, 四川 绵阳 621000)

具有时滞的Lotka-Volterra模型大量出现于生物、人口等生态领域,为学者们广泛关注和讨论,尤其是解的稳定性等渐近性质更为学者们所重视[1-11],但由于测量等误差,种群间相互作用的参数往往无法获得精确值而只知道其上下界,这时研究区间动力系统的鲁棒稳定性和部分变元鲁棒稳定性就显得非常重要.最近,文献[12]讨论了具有有限时滞的Lotka-Volterra模型的鲁棒稳定性和部分变元鲁棒稳定性,通过构造适当的Lyapunov泛函,利用区间动力系统稳定性理论,获得了具有有限时滞的Lotka-Volterra模型的鲁棒稳定性和部分变元鲁棒稳定性的充分条件;文献[13]进一步讨论具有有限时滞的Kolmogorov系统的鲁棒稳定性和部分变元鲁棒稳定性,通过构造Lyapunov泛函,利用区间动力系统稳定性理论,获得了具有有限时滞的Kolmogorov系统的鲁棒稳定性和部分变元鲁棒稳定性的充分条件.受上述文献的启发,本文研究一类具有无穷时滞的Lotka-Volterra模型的鲁棒稳定性和部分变元鲁棒稳定性,通过构造Lyapunov泛函,使用区间动力系统的稳定性理论[14],运用Lyapunov-LaSalle定理[2],给出了系统全局渐近鲁棒稳定和部分变元鲁棒稳定的充分条件.

1 预备知识

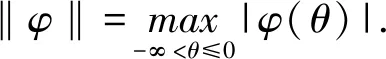
考虑如下一类参数不确定的具有无穷时滞的Lotka-Volterra模型

(1)

本文假设:

(H2) 向量或矩阵的集合为

(H3) 对任意的r∈rI,A∈AI,B∈BI,D∈DI,方程(1)存在唯一的全局正解x(t;t0,φ);

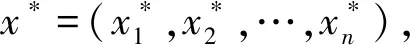
考虑自治时滞微分系统

(2)

其中,xt=x(t+θ)(-∞<θ<0),f:C→Rn是一个连续映射且f(0)=0.假设系统(2)存在唯一解且连续地依赖于初始函数.记系统(2)过(t0,φ)的解为x(t;t0,φ).

对连续的泛函V:C|→R,定义

(3)

为V沿着(2)式的解的导数.

定义 1.1设x*=(y*,z*)是系统

(4)

的平衡态,其中,x=(y,z),y=(y1,y2,…,yk),z=(z1,z2,…,zl),k+l=n.

(i) 若对任意的ε>0,t0∈R,存在δ(ε,t0)>0,使得当‖(φ,ψ)‖≤δ时,有

|y(t;t0,φ,ψ)-y*|<ε,t≥t0,

则系统(4)的平衡态x*关于变元y部分稳定.

(ii) 若对任意的ε>0,t0∈R,存在b0(t0)>0和T(t0,ε,φ),使得当‖(φ,ψ)‖≤b0(t0)且t≥t0+T(t0,ε,φ)时,有|y(t;t0,φ,ψ)-y*|<ε,则系统(4)的平衡态x*关于变元y部分吸引.

(iii) 若系统(4)的平衡态x*关于变元y部分稳定且部分吸引,则系统(4)的平衡态x*关于变元y部分渐近稳定.

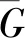
定义

M=方程(2)在E中的最大不变集.

(5)

引理 1.4[2](Lyapunov-LaSalle定理) 若V是G上的Lyapunov泛函,xt(φ)∈G是(2)式的有界解,则ω(φ)⊂M,即x(t;t0,φ)→M,当t→+∞.

2 主要结论

定理 2.1假设:

1)aii<0,i=1,2,…,n;

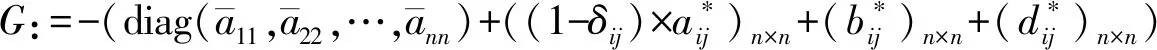
i=1,2,…,n.

(6)

因为G是M矩阵[15],所以对每一个βi>0,存在常数ci>0(i=1,2,…,n)使得

j=1,2,…,n.

(7)

构造Lyapunov泛函

(8)

由(3)式得

G={φ:φ∈C,φ(0)>0},

(9)

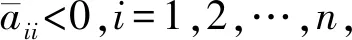
1)aii<0;

2)G:=-(diag(a11,…,ann)+((1-δij)×

|aij|)n×n+(|bij|)n×n+|dij|n×n)是M矩阵,

则确定方程

(10)

定理 2.4假设:

2) 存在常数cj>0,j=1,2,…,n,使得

(11)

j=m+1,m+2,…,n,

(12)

则系统(1)的平衡态x*关于变元x1,x2,…,xm部分鲁棒稳定,关于变元xm+1,xm+2,…,xn部分全局渐近鲁棒稳定.

证明构造Lyapunov泛函

(13)

则

(14)

所以

V(t0),t≥t0.

(15)

因为

V(t0)<∞,

(16)

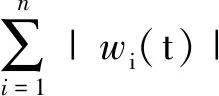
Q<∞,

(17)

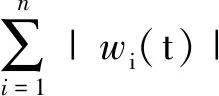
V(t0), t≥t0,

(18)

这意味着|ewj(t)-1|∈L1[0,∞).

下面,通过构造一个不同的Lyapunov泛函,得到系统(1)更方便应用的部分鲁棒稳定的充分条件.

定理 2.5假设下面成立:

(19)

(20)

其中

|aij+aji|*=max{|aij+aji|},

则系统(1)的平衡态x*关于变元x1,x2,…,xm部分鲁棒稳定,关于变元xm+1,xm+2,…,xn部分全局渐近鲁棒稳定.

证明取正常数di,i=1,2,…,n,使得

i=1,2,…,m,

(21)

i=m+1,m+2,…,n.

(22)

构造Lyapunov函数

(23)

(ewi(t)-1)(ewj(t)-1)|+

类似定理2.4的讨论可证.

(24)

i=m+1,m+2,…,n,

(25)

3 例子和数值模拟

例 3.1考虑如下2维参数不确定的具有无穷时滞的Lotka-Volterra系统

(26)

为讨论方便,不妨取

rI:={r=(0.8,0.4)T},

容易计算出

(27)

对任意的B∈BI,因为

(28)

是M矩阵,则由定理2.1,系统(26)全局渐近鲁棒稳定.

现在,使用Milstein方法[16]证实这个结果.设ξ1(θ)=0.32eθ,ξ2(θ)=0.18eθ,μ12(θ)=μ21(θ)=eθ,θ∈(-∞,0].考虑下面的离散化方程:

x1(k+1)=x1(k)+[r1+a11x1(k)+

b11x1(k-τ11/Δt)+0.09d12e-kΔt+

(29)

x2(k+1)=x2(k)+[r2+a22x2(k)+

b22x2(k-τ22/Δt)+0.16d21e-kΔt+

(30)

在图1中,取μ12(θ)=μ21(θ)=eθ,ξ1(θ)=0.32eθ,ξ2(θ)=0.18eθ,τ11=τ22=1,r1=0.8,r2=0.4,a11=-3,a22=-2.5,b11=-1.3,b22=-1,d12=-0.9,d21=-0.9,Δt=0.01,则x*=(0.171,0.070),因为G为M矩阵,由推论2.3,x*全局渐近稳定,图1证明了这个结果.在图2中取b11=-5,b22=-3,其余参数与图1相同,此时G不是M矩阵,图2表明系统(26)不稳定.

图 1 当b11=-1.3,b22=-1时系统(26)全局渐近稳定

图 2 当b11=-5,b22=-3时系统(26)不稳定