“三态”模型:化学平衡移动教学有效的教学思维模型
洪云龙
一、问题的提出
“化学平衡移动”是中学化学基本理论的重要组成部分,是化学教学的重点和难点。笔者调查发现,许多教师在教学中尽管对此内容讲授得很充分,耗费时间很长,但效果往往不尽如人意,学生仍然觉得“理论性强,思维难度较大,理解透彻较为困难”;教师尽管对学生进行了多次和较长时间的训练,但学生仍然在分析、解决平衡移动问题时感到困难、抽象,力不从心。如何改变这种教学现状,如何把这些笼统、抽象、理论性强的知识内容变得具体、形象、直观,以便于理解、掌握和运用,如何更有效地分析和解决平衡移动问题,等等,是笔者近年一直研究的课题。笔者发现,在教学中帮助学生建立有效的教学思维模型进行分析和讲解,是其中一种效果良好的方法和策略。
二、教学思维模型的研究
(一)传统教学思维模型的不足
化学平衡的移动,就是改变外界条件,破坏旧的平衡状态,建立起新的平衡状态的过程。[1]在教学中教师常常使用图1[2]的思维模型进行讲解,以帮助学生理解相关知识,分析和解决有关问题。
此思维模型只有“二态”——旧平衡态、新平衡态,故暂且命名为“二态”模型。笔者发现,此“二态”模型应用在教学中明显存在一些不足,具体为:“旧平衡态”过渡到“新平衡态”的中间过程比较笼统、抽象,学生较难把握,易被“改变条件”所迷惑,对“改变条件后隐藏着的各种变化”不能很好地挖掘,因而教学效果不甚理想。显然,很有必要建立一种具体、形象、直观的思维模型,以便于更好地理解和掌握相关知识,更有效地分析和解决有关问题。
(二)建立新的、有效的教学思维模型——“三态”模型
“三态”模型,就是为弥补“二态”模型的不足而在其“二态”(“旧平衡态”与“新平衡态”)之间虚拟、假设出一种特殊过渡状态——“瞬间态”,从而形成“三态”分析的一种有效的教学思维模型。所谓“瞬间态”,就是旧平衡在改变条件的瞬间,平衡还来不及移动时的状态。“三态”模型如图2所示。
“旧平衡态”到“瞬间态”由改变条件的瞬间造成,此时平衡还来不及发生移动。平衡发生移动实则始于“瞬间态”,终于“新平衡态”。
“三态”模型中标注的有关量可以是:浓度、体积、压强、温度、物质的量、正反应速率、逆反应速率等。其中,“瞬间态”的量由“旧平衡态”的量与“改变条件”的量两部分复合而成。
“三态”模型能变“二态”模型的笼统、抽象为具体、形象。在教学中只需引导学生比较、分析某个或某几个有关量分别在“三态”模型之中发生了怎样的变化(增大、减小或不变),就能深刻理解相关知识,成功解决有关问题。
三、“三态”模型在教学中的应用
(一)便于深刻理解勒夏特列原理
勒夏特列原理是“化学平衡移动”教学的重点和难点,其内容为:改变影响化学平衡的一个因素,平衡将向着能够减弱这种改变的方向移动。只有引导学生深刻理解勒夏特列原理,才能帮助他们熟练地运用它来解决问题。
1.如何才算是“改变影响化学平衡的一个因素”?
在教学中用“二态”模型来考察勒夏特列原理,学生往往对“改变条件”与“改变影响化学平衡的一个因素”分辨不清,理解模糊,但用“三态”模型能很好地解决这个问题。
在“三态”模型中,勒夏特列原理实际是针对“旧平衡态”与“瞬间态”而言的,是通过比较“旧平衡态”与“瞬间态”之间的某个量(浓度、温度、压强等)的变化情况来判断平衡移动方向的。改变条件后,只有导致“瞬间态”的浓度、压强、温度中的某一量真正比“旧平衡态”增大或减小了,才能算是“改变影响化学平衡的一个因素”,平衡才“向着能够减弱这种改变的方向移动”。如果表面上改变了某个条件,但实际上并不造成“瞬间态”与“旧平衡态”之间浓度、压强、温度的不同,则不算是“改变影响化学平衡的一个因素”,不会引起平衡的移动。
例如,反应2A(g)+B(g)?2C(g)在一容积可变的容器中达到平衡时,A、B、C的物质的量分别为4mol、2mol、4mol。现在恒温恒压的前提下“改变条件”:将平衡混合物中A、C减少1mol ,B减少0.5mol。这种“改变条件”算不算是“改变影响化学平衡的一个因素”呢?
在教学中若以“二态”模型来考察,很容易得出“既然是改变了条件(A、C减少1mol,B减少0.5mol),那肯定是改变了影响化学平衡的一个因素”的错误结论。但若改用“三态”模型来分析,便能排除干扰,看清真相(见图3)。
算不算是“改变影响化学平衡的一个因素”,要通过比较“瞬间态”与“旧平衡态”的浓度大小来回答。“瞬间态”A、B、C的物质的量分别为3mol、1.5mol、3mol,“旧平衡态”A、B、C的物质的量分别为4mol、2mol和4mol。“瞬间态”A、B、C的物质的量之和是“旧平衡态”A、B、C的物质的量之和的倍,故恒温恒压下“瞬间态”的容器体积亦应是“旧平衡态”的倍,用c=n/V进行计算,得知“瞬间态”A、B、C的浓度分别与“旧平衡态”A、B、C的浓度对应相等,即浓度不改变,且已知温度和压强亦不改变,故不算“改变影响化学平衡的一个因素”,平衡不发生移动。
2.化学平衡移动有关量将如何变化?endprint
勒夏特列原理告诉我们:平衡移动的结果只是“减弱这种改变”,但不能“抵消这种改变”。有些同学对此感到抽象,难以理解,且看教学中如何用“三态”模型来直观地表示这个问题(图4为增大某一因素后“三态”有关量的变化、图5为减小某一因素后“三态”有关量的变化)。
从图4、图5可以看出,增大(或减小)某一因素后,“瞬间态”的有关量(浓度、压强、温度等)比“旧平衡态”增大(或减小)得很多,平衡移动后,“新平衡态”的有关量虽然比“瞬间态”减小(或增大)了,但不会恢复回“旧平衡态”,仍然比“旧平衡态”大(或小),只是增大量(或减小量)变少了一些而已。所以说,平衡移动的结果只是“减弱了这种改变”,但不能“抵消这种改变”。因此,“新平衡态”的相应量应介于“旧平衡态”与“瞬间态”之间,即量的关系是:“旧平衡态”<“新平衡态”<“瞬间态”;或“瞬间态”<“新平衡态”<“旧平衡态”。
(二)便于系统总结和深刻理解判断平衡移动方向的各种方法
判断平衡移动的方向,究竟有哪些方法?在教学中只须引导学生认真研究“三态”模型,便会发现,平衡移动方向的判断实际就是任意“二态”的比较,即只需比较任意“二态”之间的某个或某几个有关量的大小,便能成功判断平衡移动的方向。这为我们系统总结更多判断方法,并从一定高度上理解和掌握这些方法提供了很好的思路。任意“二态”共有3种组合:“旧平衡态”与“瞬间态”、“瞬间态”与“新平衡态”、“旧平衡态” 与“新平衡态”。据此可总结出5种判断方法(见图6)。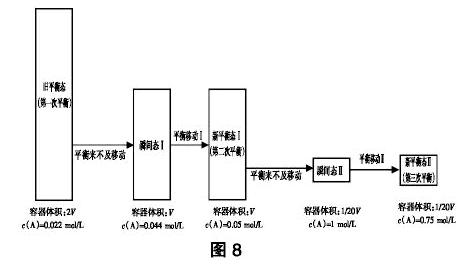
1.“旧平衡态”与“瞬间态”之间的判断方法
方法1:勒夏特列原理
在“三态”模型中的实质:
如前所述,是通过比较“瞬间态”与“旧平衡态”的浓度、压强、温度中的某一量的大小来判断平衡移动方向的。
方法2:化学反应速率角度
在“三态”模型中的实质:
通过比较正、逆反应速率由“旧平衡态”变为“瞬间态”的变化程度的大小,进而推知“瞬间态”的正、逆反应速率的相对大小来判断平衡移动的方向。
若“瞬间态”的正反应速率>“瞬间态”的逆反应速率,平衡正向移动;若“瞬间态”的正反应速率<“瞬间态”的逆反应速率,平衡逆向移动;若“瞬间态”的正反应速率=“瞬间态”的逆反应速率,平衡不移动。
2.“瞬间态”与“新平衡态”之间的判断方法
方法3:化学平衡常数角度
在“三态”模型中的实质:
通过比较“瞬间态”的浓度商Q与“新平衡态”的化学平衡常数K的相对大小来判断平衡移动的方向。
当“瞬间态”的Q <“新平衡态”的K时,平衡正向移动;当“瞬间态”的Q >“新平衡态”的 K时,平衡逆向移动;当“瞬间态”的Q =“新平衡态”的K时,平衡不移动。
例如,对于某一吸热反应,处于旧平衡态时,浓度商本来等于化学平衡常数,升高温度后,虽然“旧平衡态”变为“瞬间态”时浓度商保持不变,但“旧平衡态”转为“新平衡态”时化学平衡常数却变大了(变大了的平衡常数显然应是“新平衡态”的平衡常数,须用“新平衡态”而非“旧平衡态”的平衡常数来与“瞬间态”的浓度商进行比较判断),导致Q 方法4:同种物质前后量的比较 平衡发生移动实则始于“瞬间态”,终于“新平衡态”。所以,可以通过比较同种物质在“瞬间态”与“新平衡态”之间的量的变化(变多、变少或不变)来判断平衡移动的方向。 例如,反应aA(g)?bB(g)在一密闭容器中达平衡后,保持温度不变,将容器体积增加一倍,当达到新的平衡时,B的浓度是原来的60%,此时平衡将如何移动呢?我们可以通过比较气体B在“瞬间态”与“新平衡态”之间量的变化来判断(见图7)。 “瞬间态”、“新平衡态”气体B的浓度分别是50%cB、60%cB,而容器体积均是2V,用公式n=cV进行计算,得知平衡从“瞬间态”移动到“新平衡态”时气体B变多了,故平衡正向移动。 3.“旧平衡态”与“新平衡态”之间的判断方法 方法5:同种物质前后量的比较 通过比较同种物质在“旧平衡态”与“新平衡态”之间量的变化(变多、变少或不变)也能判断平衡移动的方向。 例如在图7中,我们亦可通过比较气体B由“旧平衡态”变为“新平衡态”时量的变化来判断平衡移动的方向。因为“旧平衡态”、“新平衡态”气体B的浓度分别是cB、60%cB,而容器体积分别是V、2V,用公式n=cV进行计算,得知“旧平衡态”变为“新平衡态”后气体B变多了,故亦可推出平衡正向移动。 (三)便于突破解题上的思维障碍 在习题教学中,若能指导学生运用“三态”模型来分析平衡移动问题,那么一些抽象、复杂、疑难的问题将变得形象、简单、直观,从而有利于突破解题上的思维障碍。这是“三态”模型最能凸显应用价值的一个方面。 例 在温度为t℃、压强为1.01×106Pa的条件下,某密闭容器内,下列反应达到化学平衡:A(g)+B(g)?3C,测得此时c(A)=0.022mol/L;压缩容器使压强增大到2.02×106Pa,第二次达到平衡时,测得c(A)=0.05mol/L;若继续压缩容器,使压强增大到4.04×107Pa,第三次达到平衡时,测得c(A)=0.75mol/L。则下列关于C物质状态的推测正确的是( ) A. C为非气态 B. C为气态 C. 第二次达到平衡时C为气态 D. 第三次达到平衡时C为非气态 解析:此题看似复杂、抽象,但运用“三态”模型能很好地突破思维障碍(见图8)。
压缩容器使压强由1.01×106Pa增大到2.02×106Pa,“瞬间态Ⅰ”的容器体积应是“旧平衡态”的倍,故“瞬间态Ⅰ”的c(A)应是“旧平衡态”的2倍,为c(A)= 0.022mol/L×2 =0.044mol/L,又知“新平衡态Ⅰ”c(A)=0.05mol/L,且“新平衡态Ⅰ”与“瞬间态Ⅰ”的容器体积相等,可知“瞬间态Ⅰ”变为“新平衡态Ⅰ”时气体A的物质的量增多了,故推知平衡逆向移动。因为增大压强平衡逆向移动,根据勒夏特列原理,逆向移动方向应是气体体积减小的方向,即气体生成物的化学计量数之和应大于气体反应物的化学计量数之和,故物质C只能是气态。继续压缩容器使压强增大到4.04×107Pa,得“瞬间态Ⅱ”,“瞬间态Ⅱ”的容器体积应是“新平衡态Ⅰ”的倍,故“瞬间态Ⅱ”c(A)应是“新平衡态Ⅰ”的20倍,为c(A)=0.05mol/L×20 =1 mol/L,比“新平衡态Ⅱ”的c(A)=0.75mol/L大,且“瞬间态Ⅱ”与“新平衡态Ⅱ”的容器体积相等,可知“瞬间态Ⅱ”变为“新平衡态Ⅱ”时气体A的物质的量减少了,故平衡正向移动,气体反应物的化学计量数之和应大于气体生成物的化学计量数之和,推知物质C应为非气态。答案:CD。
四、教学反思
为什么我们会普遍感到“化学平衡移动”知识抽象?笔者认为,这与传统的“二态”模型有相当大的关系。具体地说,“二态”模型的笼统、抽象在很大程度上导致了“化学平衡移动”的知识抽象。倘若在教学中能用形象、直观的“三态”模型来分析、讲解,那么“化学平衡移动”的抽象将不复存在,学习知识将变得简单易懂。从这个意义上看,在教学中运用“三态”模型,可以说是抓住了“化学平衡移动”教学的关键,找到了提高教学效果的方法和策略。笔者曾在高二重点班的“化学平衡移动”教学中仅运用“二态”模型,而在普通班中运用“三态”模型,两班对比,效果迥异。重点班学生普遍反映知识抽象、思维难度较大;而普通班学生反而觉得直观易懂、学好并不是很难。这证明“三态”模型的教学效果明显优于“二态”模型。
总之,在教学中运用“三态”模型,利于形象、直观地理解知识和解决问题,不失为“化学平衡移动”教学效果良好的一种方法和策略。
参考文献:
[1] 王祖浩.普通高中课程标准实验教科书·化学反应原理(选修)[M].南京:江苏教育出版社,2014:52.
[2] 王朝银.步步高·高考总复习·新课标·化学[M].哈尔滨:黑龙江教育出版社,2011:159.endprint

