一道函数零点问题的处理策略

☉陕西省靖边中学 马海生

对于函数的零点个数及所在区间的问题，最让学生和教师感到头疼的是如何来寻找合理且有效的点a与点b，使得（fa）·（fb）＜0.其实，这类问题还是有规律可循的，只要我们能逐步探索出其规律，就能找到行之有效的方案，本文就如何取点a与b作一探讨，让零点问题不再神秘.

【知识概要】

零点存在定理：如果函数y=f（x）的图象是一条连续不断的曲线，若f（a）·f（b）＜0，则函数在区间（a，b）上至少存在一个零点.

思路1：直接取点

思路2：放缩取点

有时我们可以通过对给定的函数表达式进行放缩，然后再取特殊点来进行判断.放缩的手段通常有：利用常见的不等式；对表达式的一部分进行放大或缩小；在某种限制条件下放缩等.

思路3：调整取点

我们先选取一个值来进行判断，如果可行则万事皆休；如果不可行，则可以在这个值上作出一些调整再去判断，如此下去，总能找到一个可行的值出来.

题目：已知函数

试问：过点P（0，2）可作多少条直线与曲线y=f（x）相切？并说明理由.

分析：设过点P的直线l与曲线y=f（x）相切于点Q（x0，f（x0）），

因为切线过点P（0，2），

先对g（x）求导，可得

分类讨论：

①当a≤0时，g′（x）＜0，函数y=g（x）在（0，+∞）上单调递减，y=g（x）至多只有一个零点.

猜测函数只有一个零点，现在去寻找两个值m，n，使g（m）＜0，g（n）＞0.

所以取x=e即满足条件.

②当a＞0时，由

即g（x）在区间上单调递减，

由lnx≤x-1＜x，可得

然后，猜测函数有两个零点，现在只需要找m和n，使得

换个角度，使alnx-a-2=0，则

令x，此时，还是不对，有可能小于零！那么呢，行吗？

事实告诉我们，还是不行！那么问题出在哪儿？真的不能这样处理吗？

进一步改进！显然分母是一次多项式已经不可行了，调整为二次！

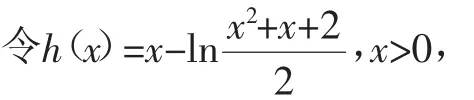
对h（x）求导，可得故h（x）在区间（0，+∞）上单调递增.

所以h（x）＞h（0）=0，结论成立.

变题：已知a∈R，求函数f（x）=2x-alnx-a-2的零点个数.

分析：先对函数求导，可得

分类讨论：（1）当a≤0时，f′（x）＞0，则f（x）在（0，+∞）上单调递增，

所以f（x）的零点个数至多有一个.

所以f（x）在（0，+∞）上有且只有一个零点.

（2）当a＞0时，令f（′x）=0，得

判断函数有两个零点！现在找m，n，使得n，且f（m）＞0，f（n）＞0.

先取特殊值，令n=ea，则，且有（fe）a=2ea-a2-a-2，可证得f（ea）＞0.

考虑令-alnx-a-2=0，则

所以当a＞0时，f（x）在（0，+∞）上有两个零点.

方法总结：对于此类难题的处理，一般没有现成的规律和方法可循.我们只能通过一些手段去探求问题的正确思路.比如：①化归，尝试着将问题转化为一个我们较为熟悉的问题或者是另外一种表达方式，看看是否有益于寻找正确的解题思路；②结合已知的表达式，弄清影响函数取值的主要因素，合理且有效地去猜测、验证、调整、再验证，必要的话，不断重复这样的过程；③结合常见的不等式去放缩，看看是否对解题有所帮助；④联想以前是否有过类似的问题，当时的解法是否有用或者改进后是否有用.通过这些手段，总能使问题得到解决.