基于“开展探究式教学，发展核心素养”的探究——以“三角形重心教学”为例

☉北京市密云区第二中学 王德臣

一、问题的提出

数学核心素养是一个人经过数学教育培训后所具有的数学特质.正如高中数学课程标准所述：“会用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言描述现实世界.”这是一个人通过数学学习逐步形成的关键能力和必备品质，也是基本知识、基本技能、基本思想及基本活动经验的综合体现.

重心是中学数学及物理学中的重要概念.三角形的重心是研究几何图形重心的基础，能够用尺规作图及坐标运算等方式进行研究.在用点的坐标来研究三种不同形态的三角形的重心的探究活动的教学设计中，我们要解决以下四个问题：重心的意义是什么？构成“三角形”的要素是什么？构成“三角形”的要素与重心之间有怎样的关系？确定“三角形”重心的方法及研究过程，以及对探究其他几何图形的重心有哪些指导意义？

二、以“三角形重心”教学为例，实施探究式教学

教师：在平面几何中，三角形的重心是如何定义的？

学生：三角形三条中线的交点是三角形的重心.

教师：在解析几何中，若△ABC的三个顶点分别为那么，重心G的坐标公式是什么？

学生：三角形的重心G的坐标为

教师：这个结论是正确的吗？三角形的重心公式的含义是什么？

设计意图：新知识的学习必须以学生已有的认知结构为基础，从学生已有的知识出发，提出富有挑战性的问题，激发学生的学习兴趣，使学生积极主动地参与到课堂学习之中，从而引发学生的理性思考、批判和质疑.

教师：为了回答上述问题，请同学们思考以下问题.

问题1：生活中的三角形有哪些呈现方式？如何理解数学中的三角形？

设计意图：打破学生的原有认知，激发学生思考三角形的其他呈现形态.引导学生观察生活现象并从中抽象出数学模型，理解三角形点系、三角形框架结构及常规三角形（面）的概念，初步认识到三角形的构成要素决定了三角形的重心（性质）.

学生：列举生活实例，交流各种三角形的模型.

教师：三角形有三种呈现形式，第一种是由三个点构成的“点系三角形”，第二种是由三条边构成的“边系三角形”，第三种是教材中提到的三角形，它是由三角形的平面构成的“面系三角形”.本节课重点研究不同形态的三角形的重心的求法，并比较各个重心公式的异同点.

问题2：平面内有质量相同的三个点A（x1，y1），B（x2，y2），C（x3，y3）组成的点系，则三点系Ω={A，B，C}的重心为

设计意图：数学的课堂教学不是单一地传授知识，更重要的是让学生体验获取知识的过程.在具体问题的引导下，学生通过探究设计解决问题的方案，用数学语言表达、推理与运算，用数学方法解决问题，从中培养学生数学建模、逻辑推理、数学运算的数学核心素养.

学生：分组讨论解决问题的方案，并给予证明.

证明：因为点系Ω1={A，B}的重心为点系Ω={A，B，C}的重心是点系Ω2={Ω1，C}的重心G（x，y），其中所以命题成立.

教师：听取学生的解题方案，给予学生适当的指导，最终达成共识，学生给出证明.

总结提升：利用转化思想，先求出其中任意两个点的重心G1，再求出G1和第三个点的重心G，从而把三个点的重心转化成两个点的重心，所得结论与平面三角形的重心公式一致.

问题3：若△ABC由三条粗细质地均匀的三条线段构成，其中三个顶点的坐标分别为A（x1，y1），B（x2，y2），C（x3，y3），则此“边系三角形”的重心G（x，y）满足：

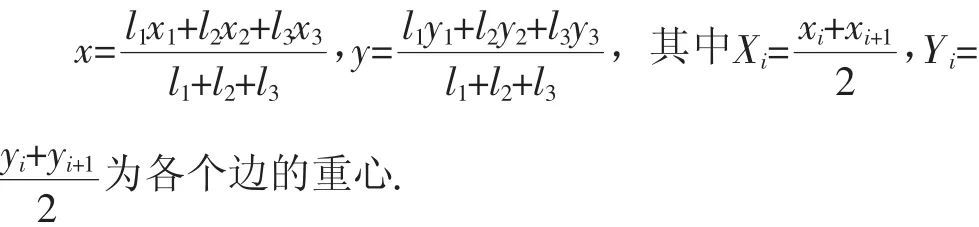
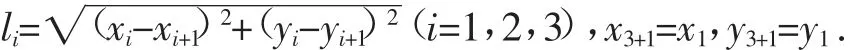
设计意图：通过层层递进的变式探究，激发更多学生的主动参与，学生的思维越来越活跃，通过各种解题方案的提出，解决问题的脉络也越来越清晰，学生头脑中的认知结构不断被激活，创造性的思想源源不断涌出，身在课堂，乐在其中.

学生：设计解题方案，确定解题思路，把“边系三角形”的重心转化成三条边的中点够成的“点系三角形”的重心.

图1

证明：为了便于书写，不妨设AB=l1，BC=l2，CA=l3，因为线段l1的重心是线段AB的中点线段l的重心2为其中点线段l的重心为其中点3各个点的质量与对应线段的长度成正比 ，设 线 段MN的 重 心 为Q（x0，y0），则x0=

点Q（x0，y0）的质量与l2+l3成正比，线段PQ的重心G（x，y）为△ABC的重心，则：

教师：引导学生对问题的结论做进一步的总结，并抽象出一般结论，“边系三角形”的重心是各个边的中点坐标与对应边长的加权平均值.

三、活动反思

“定性”与“定量”是数学几何学中研究的重点与难点，本节课的教学设计思路表面上看是研究三角形的重心公式，是定量的问题，实则是从“三角形”的构成要素出发，最终发现不同形态的“三角形”的重心公式的实际含义，是“定性”的问题，从“定性”的角度看各个形态的三角形的重心是相同的.通过学生的探究活动，学生获得了一定的数学基础知识、基本技能、基本思想和基本活动经验，进一步完善了学生的认知结构，感悟到数学的理性精神，从而提升了学生的数学核心素养.

章建跃在《数学教育随想录》中说：“要数学地认识事物，其基本结构是：定义概念——推导性质——建立联系——实践应用.定义概念从而明确数学对象；探索对象的要素与要素、要素与环境之间的关系和相互作用而获得性质；通过建立相关知识的联系而形成知识体系；应用所得知识解决数学的内外问题，并深化知识，拓展新知.这是一个螺旋上升、逐渐深入的过程”.本节课依托上述理论，从生活中的实际问题出发，定义了不同形态的三种“三角形”，并研究它们的重心与构成要素之间的关系，以及三种形态的三角形的重心之间的关系.

探究式教学的关键是问题串的设计，问题串应由浅入深、环环相扣，符合学生的最近发展区，每一个问题都富有挑战性，使得不同层次的学生凭借自己的生活经验及知识经验都能够积极地参与到探究活动之中，都有“发现”及“表现”的机会，通过生活观察、独立思考、逻辑推理、代数运算、转化与化归、几何直观及数形结合等数学思维的基本形式，最终形成统一的共识，使学生真正理解“三角形”重心的意义，并在探究过程中提升解题能力，丰富思维品质.（本文得到首都师范大学王安教授的悉心指导，并向王教授致谢）