“问题链”导向教学——以线性规划为例

☉浙江省玉环市玉城中学 张夏飞

数学是研究自然社会中存在的逻辑和数量关系的学科，数学产生于人们对自然现象的疑问，又被好奇心和思考推动着发展.从本质上来说，数学就是一门围绕“问题”展开的学科，综合了解决和提出问题的思想方法，以及对部分问题的回答.问题能够激发研究者探索的欲望，并且提供了一种精力和思考方向的聚焦，能极大地推动研究的进程，同样的，问题也能引起学生的兴趣，巧妙设计的问题还能让学生在探索与思考中抓住知识结构中的重点.所以，教师可以尝试以“问题”为线索展开课堂教学，将教学内容按照类别及难度等进行划分，并结合教学大纲和自己的教学思路，总结出具有导向性的问题，并利用问题传导概念，利用问题激发思考，利用问题引导学生探索数学的本质，同时，教师还可以设计一连串的问题，组成问题链，这样更能系统地提升学生的学习效果.下文中笔者就将结合自身的教学实践，以线性规划中用二元一次不等式表示平面区域这一节的教学为例，和读者分享自己在这方面的经验.

线性规划是一个非常重要的知识点，它综合了不等式、解析几何及方程组的知识，对提高学生的思维能力也有着很大的作用，在生产生活中，线性规划的思想方法也被广泛应用于资源分配等场景中.在高中阶段，用二元一次不等式组表示平面区域是学生最先接触到的线性规划知识，其中涉及了许多基本的概念，也涉及了数形结合、分类讨论及转化与化归等思想方法，是线性规划的入门知识.用二元一次不等式组表示平面区域这一模块建立在学生掌握不等式及基本解析几何知识的基础上，从概念性的知识来说并没有太多需要补充的地方，真正需要学生深入思考和学习的是知识之间的联系，以及如何用这样的方法实现规划目标，因此，笔者设计了如下的问题链来帮助学生建立知识体系.

一、“问题链”导向教学的具体过程

问题一：若已知某工厂有A种原料10吨，B种原料60吨，现市场对甲、乙两种商品有所需求，如果每生产一吨甲类产品需耗费A种原料4吨，B种原料12吨，能带来2万元的收益，每生产一吨乙类产品需消耗A种原料1吨，B种原料9吨，带来的收益为1万元，（上述信息见下表1）试问：在不超过原料限制的情况下，如何分配资源生产可以使得工厂的收益最高？

表1

问题转化：根据学生的知识水平，教师可以引导他们列出如下的不等式组.

设生产甲类产品x吨，生产乙类产品y吨，设总利润为P万元，则根据题设可得出不等式组：故将问题转化为在上述不等式组的约束下，求P=2x+y取最大值时，对应的x，y分别为多少.

设计意图：这是一道非常典型的线性规划类题目，需要用到数形结合等经典方法，通过设计这道题，笔者希望能让学生在不等式与直线区域之间建立起认知联系.在本题中，不等式4x+y≤10可以理解为两个条件，即4x+y=10和4x+y＜10，等式的几何意义比较容易理解，即为直线y=10-4x上的点，学生需要理解的是4x+y＜10的几何意义，于是为了帮助学生理解，笔者从直线方程的本质入手，设计了如下的题目.

问题二：假设在平面直角坐标系中有这样一条直线，试问和这五个点与直线l之间存在怎样的位置关系？点与直线的位置关系在代数层面上是如何体现的？能否根据上述结论，通过代数的方法，判断点F（3，-2.1）与直线l的位置关系？

设计意图：学生之前接触的大多数是直线上的点，很少关注直线外的点与直线的具体位置关系，通过设置一系列横坐标相同，纵坐标不同的点，学生会不由自主地关注到横坐标相等时，纵坐标的差别带来的位置变化，比如在本题中，D点和E点的横坐标都是2，由于纵坐标不同，它们分别位于直线的上下两侧.这个问题通过特殊的例子，让学生开始思考坐标与位置之间的关系，为后续进一步深入的思考打下了基础和铺垫.

问题三：承接问题二，有哪些点是在直线l的下方？有哪些点是在直线l的上方？对于同一侧的点，它们的横坐标与纵坐标之间有什么样的数量关系？

设计意图：通过聚焦同一位置的点的横坐标与纵坐标的数量关系，引导学生去思考不等式与平面区域之间的关系，并对一般规律做出一定的假设.

问题四：通过上述问题，你能否证明，点的横坐标与纵坐标满足不等式y＜10-4x是该点在直线y=10-4x下方区域的充分必要条件？（如图1所示）

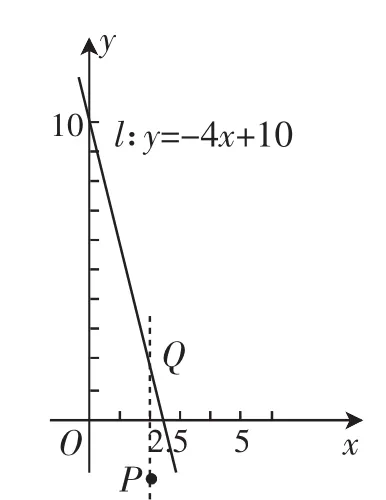
图1

问题解答：能证明.充分性：假设任意一点P（x0，y0）满足不等式y＜10-4x，则y0＜10-4x0，取直线y=10-4x上一点Q（x0，y1），则y1=10-4x0，且易知y1＞y0，在坐标图上表现为点P在点Q的下方，因此，满足不等式的点一定位于直线l的下方.必要性：取直线l下方的一点P（x0，y0），再取直线上与P横坐标相同的一点Q（x0，y1），由图1可知，在横坐标相等的情况下必有y0＜y1=10-4x0，满足不等式.

设计意图：问题二和问题三利用特殊情况激起了学生的思考，让学生对不等式的几何意义形成初步印象，问题四的设计是对零散示例的总结，让学生从理论的角度证明了一般规律，充分性证明帮助学生由代数关系过渡到几何关系，必要性证明帮助学生从几何关系的角度理解代数关系，将满足不等式的解与直线下方的点一一对应起来.

问题五：从问题四的结论中，推断y＜kx+b及y＞kx+b分别表示怎样的区域？

设计意图：由例子抽象到更一般的规律，为后续教学做铺垫.

问题六：试画出直线3x+y+1=0的图像，并用阴影表示出不等式3x+y+1＞0的区域，尝试总结出二元一次不等式Ax+By+C＞0（B≠0）代表的平面区域与A，B，C之间的关系.

设计意图：加深学生对所学概念的理解，让学生学会利用转化与化归思想，将更一般的情形转化为熟悉的情形，以便解决更普遍的问题.

问题七：试将下列不等式表示的平面区域在同一个直角坐标系中表示出来：（1）4x+3y＜20；（2）y≥0；（3）x≥0.同时思考，第一问中约束不等式的解和公共区域有什么关联？

设计意图：问题七的设置主要有两个目的，第一，结合了三种不同的情况，让学生得以巩固所学知识并加深理解；第二，呼应教学开始时的例题，达到首尾呼应的效果，同时让学生将不等式表示的区域画在同一个直角坐标系中，这样能激发他们思考公共区域与不等式组解集的关系，为接下来的教学埋下伏笔.当然，教师不用在这里就急于强调解集与公共区域的具体关系，因为这有可能会让学生觉得信息量大，难以接受.

问题八：尝试用不等式组表示图2和图3中的阴影部分.

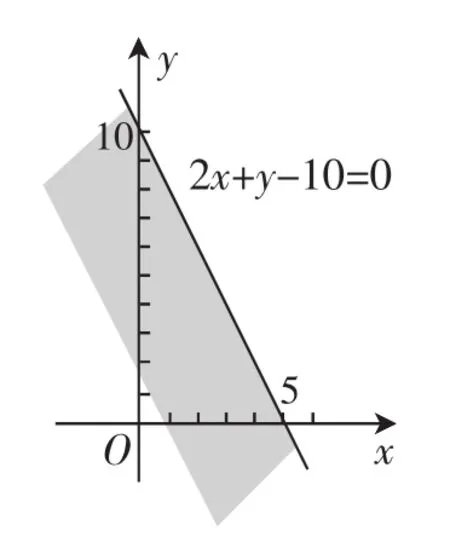
图2

图3

设计意图：之前的例题都是让学生从不等式过渡到几何区域，补充这个问题可以让学生换一种视角来思考问题，能让学生更全面、更透彻地理解知识，同时，笔者还补充了一些检验区域是否画对的方法，比如特殊点检验法、平移法等，让学生能更灵活精确地解决此类问题.

二、教学总结

在问题链的设计方面，笔者认为有以下几点需要注意：首先，问题链应该服务于教学内容，比如在线性规划的教学实践中，笔者设计的问题都是为了让学生理解相关概念；其次，问题链的设计要有梯度，要结合学生的知识水平与认知特点，由具体到抽象，由特殊到一般；接着，问题链中的问题应具有明确的主题，要让学生明白问题的意义所在；最后，问题链的根本目的是引导学生思考与探索，因此要留给学生足够的思考空间.