固定网格中基于边界描述的CAD模型快速分析方法
李心耀,张卫红,陈亮
西北工业大学 工程仿真与宇航计算技术实验室,西安 710072
固定网格与传统贴体网格的最大区别在于其采用独立于结构模型的规则网格,将传统有限元分析中的网格划分问题转换为单元识别问题[1-2]。实现单元识别的前提就是能够快速地判断固定网格中任意一个节点是否位于CAD模型区域之内,然后根据一个单元所包含所有节点的位置确定单元的属性。如果一个单元或者被细化而成的子单元所包含的节点分别位于CAD模型之内和之外,则该单元或该子单元需要采用四叉树或八叉树技术进行细化。
目前,用来实现固定网格中节点属性判断的方法主要有2种:一种是采用隐式函数描述CAD模型,通过函数在固定网格中每一个节点处的正负值来判断该点的位置[3-6];另一种是采用像素模型描述CAD模型,通过密集分布的像素点来识别固定网格中任意一个节点的位置[7-9]。然而,这2种方法都不能直接利用通过设计软件建立的结构CAD模型,均需要对CAD模型进行重构,且对于复杂结构重构困难、费时。
本文研究的基于边界描述的CAD模型在固定网格中的快速单元识别方法不同于现有的单元识别方法,它直接利用设计软件建立的CAD模型信息,避免了对CAD模型进行重构的操作,降低了模型转换过程中可能造成的精度损失,同时也降低了固定网格中单元识别的难度。结合加权B样条有限胞元法,本文建立了一种固定网格中由结构CAD模型转换成有限元分析模型,进而完成有限元仿真计算的新的设计框架。
1 CAD模型至分析模型的快速转换
1.1 CAD模型的边界描述法
在计算机辅助设计软件中,CAD模型的常用描述方法有边界表示法,构造实体几何法,单元分解表示法和特征表示法等[10]。其中采用边界表示法描述CAD模型时,模型的相关数据都可以显式地给出,有利于后续的数控加工和3D打印等操作。STL格式是CAD模型边界表示的一种重要方法,它采用若干个三角面片来近似CAD模型的边界,同时这些三角面片的法向量和顶点坐标可以直接获得。以一个带孔立方体为例,在给定近似精度的前提下,它可以利用包含96个三角面片的STL格式进行表示,如图1所示。

图1 带孔立方体的CAD模型及其STL格式Fig.1 CAD model of cube with hole and its STL format
1.2 基于射线交点法的模型转换
1.2.1 射线交点法原理
空间任意一点P(xP,yP,zP)与前述带孔立方体(STL格式)的位置关系如图2所示。在笛卡尔坐标系中,以点P为起点,沿x轴正向作一条射线LP,统计射线LP与带孔立方体的交点的个数,并记为nc。

图2 任意一点P与带孔立方体的位置关系Fig.2 Relative position between point Pand cube with hole
若nc为偶数,则点P位于带孔立方体的外部;若nc为奇数,则点P位于带孔立方体的内部。另外,点P位于带孔立方体边界上的情况可以通过坐标比较等方式确定。
1.2.2 交点统计原则
点与多边形的位置关系判断是计算机图形学的基本问题之一,国内外相关学者对此进行了深入的研究[11-13],相关技术发展较为成熟。比较而言,点与多面体的位置关系判断是点与多边形位置关系判断的延伸和拓展。然而,增加的一维空间使得点与多面体的位置关系判断变得更为困难。目前,点与多面体位置关系判断的方法主要有以下几种:Kalay[14]、Lane[15]和 Horn[16]等分别提出通过分解或降维的算法实现点与多面体位置关系的判断,但是这些方法应用较为复杂,并且容易出现奇异现象。像素空间法[17]通过密集分布的像素点来识别待判断点的位置。八叉树法[18]借助对空间的逐层划分进行点的位置判断。二元空间划分方法[19]通过对空间信息进行分类来判断点的位置。基于Jordan曲线定理的方法[20]是应用最普遍的一种方法,它通过统计从待判断点沿任意方向所引射线与多面体交点个数的策略实现点与多面体相对位置的识别。Feito-Torres方法[21-22]借助待判断点,将多面体拆分为多个四面体,然后基于这些四面体的符号体积实现点的相对位置信息判断。文献[23]对上述方法进行了详细的比较,并对每一种方法的优缺点和适用范围进行了阐述。
本文基于结构CAD模型的STL格式中三角面片的顶点和法向量信息,在Jordan曲线定理方法的基础上,提出了向量运算和坐标参数相融合的算法,解决了Jordan曲线定理方法中射线过顶点、边或面(共面)时,需要重新确定射线方向的问题,实现了初始射线与三角面片任意相交情况的判定。
1)一般情形
假定△ABC是任意一个结构CAD模型的STL格式中的任意一个三角形,A(xa,ya,za)、B(xb,yb,zb)、C(xc,yc,zc) 和 n△ABC分 别 为△ABC的顶点和法向量。在笛卡尔坐标系中,一般情形下射线LP与△ABC的相交情况如图3所示。

图3 一般情形下射线LP与△ABC的相交情况Fig.3 Intersection between LPand△ABC in common situation
如图3所示,P0为射线LP与 △ABC的交点。如果P0位于 △ABC内部,则向量可以由向量表示,其数学表达式为
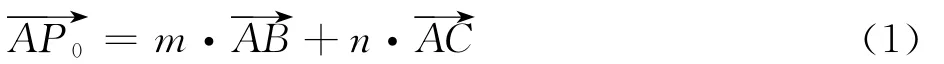
式中:0≤m≤1,0≤n≤1,0≤m+n≤1。
另外,射线LP的参数化方程可以表示为

式中:k≥0,nx= (1,0,0)。
根据式(1)和式(2)可得
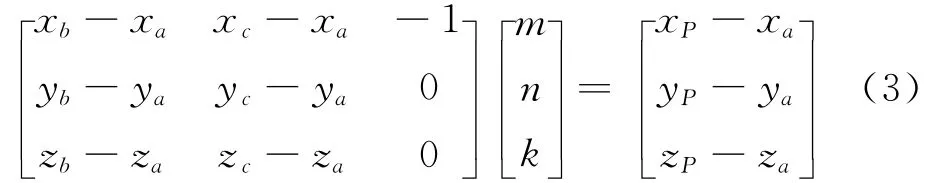
求解式(3),可得m,n和k的值如表1所示。表中,类别Ⅰ中P0位于△ABC的内部,因此记射线LP与△ABC之间有1个交点。类别Ⅳ中,可以直接确定P0位于结构CAD模型的边界上。类别Ⅱ和Ⅲ中,P0位于△ABC的一条边或一个顶点上,需要进行深入的讨论。

表1 m、n和k的取值与P0的位置Table 1 Values of m,n,kand positions of P0
2)交点位于三角形的一条边上
由CAD模型的STL格式可知,三角形的任意一条边都同时属于相邻的2个三角形,也就是说当P0位于△ABC的一条边上时,它同时也位于与△ABC相邻三角形的边上。如图4所示,2个相邻的三角形T1和T2,其法向量分别为nT1和nT2。nx= (1,0,0)为沿x 轴正向的单位法向量。
计算得到向量nT1和nx之间的夹角θ1,向量nT2和nx之间的夹角θ2。根据θ1和θ2之间的关系,可以得到此种情况下射线与三角形之间的交点统计方法如下:①θ1和θ2均为锐角或钝角时,记射线与CAD模型在此处有1个交点;②θ1和θ2分别为锐角和钝角时,无交点。

图4 交点位于三角形的一条边上Fig.4 Intersection lies on one edge of triangle
3)交点位于三角形的一个顶点上
由CAD模型的STL格式可知,三角形的任意一个顶点至少属于相邻的3个三角形,也就是说当P0位于△ABC的一个顶点上时,它同时也位于与△ABC共顶点的相邻三角形的顶点上。如图5所示,共顶点的4个三角形T1、T2、T3和T4,其法向量分别为nT1、nT2、nT3和nT4。
计算得到向量nT1和nx之间的夹角θ1,向量nT2和nx之间的夹角θ2,向量nT3和nx之间的夹角θ3,向量nT4和nx之间的夹角θ4。根据θ1、θ2、θ3和θ4之间的关系,可以得到此种情况下射线与三角形之间的交点统计方法如下:①θ1,θ2,θ3和θ4均为锐角或钝角时,记射线与CAD模型在此处有1个交点;② 其他情况,无交点。
4)射线与三角形位于同一个平面上
连接点P与△ABC的任意一个顶点(例如:顶点A),得到向量,如果向量与△ABC的法向量n△ABC之间是正交关系,则可以确定点P与△ABC位于同一个平面上。此时,可以分以下几种情况进行讨论:
当点P在△ABC内部时,式(1)可以写成如下矩阵形式:

式中:0≤m≤1,0≤n≤1,0≤m+n≤1。
为了方便对式(4)的解的讨论,定义

图5 交点位于三角形的一个顶点上Fig.5 Intersection lies at one vertex of triangle
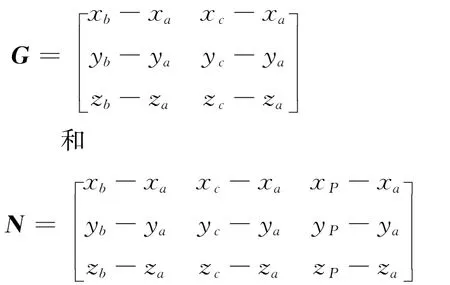
若矩阵G的秩为2,并且矩阵N的秩也为2,则式(4)有唯一解。同时,若此唯一解满足0≤m≤1,0≤n≤1和0≤m+n≤1的条件,则可以确定点P位于结构CAD模型的边界上。
当点P位于△ABC外部时,若点P在△ABC的右侧,此时射线LP与 △ABC无交点。因此,只需考虑点P位于△ABC左侧的情况,如图6所示。
实际上在结构CAD模型的STL格式中,射线LP可能会同时与多个三角形共面,如图7所示。
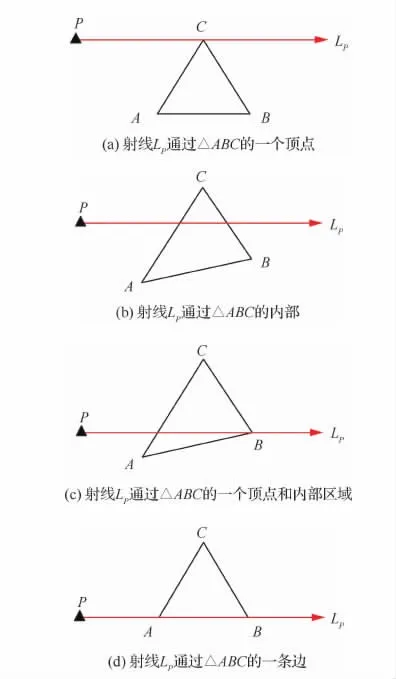
图6 点P位于△ABC的左侧Fig.6 Point Plies on the left side of△ABC
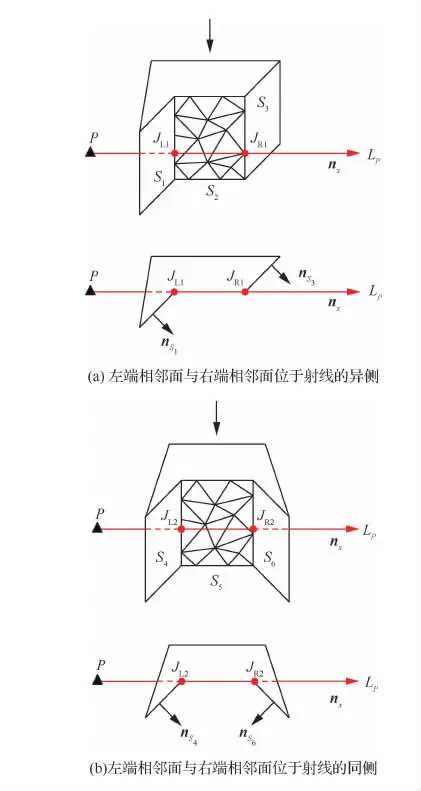
图7 射线与三角形共面情况的两种分类(除了共面曲面外,其余曲面上的离散三角形未画出)Fig.7 Two different categories of coplanar situation of ray and triangle (Besides on coplanar surface,discrete triangles on other surfaces are not plotted)
图7 (a)中,S2是与点P共面的曲面,S1和S3分别是与S2左相邻和右相邻的曲面,nS1和nS3分别为面S1和S3的法向量。JL1是射线LP与面S2在最左侧的交点,JR1是射线LP与面S2在最右侧的交点。图7(b)中,S5是与点P共面的曲面,S4和S6分别是与S5左相邻和右相邻的曲面,nS4和nS6分别为面S4和S6的法向量。JL2是射线LP与面S5在最左侧的交点,JR2是射线LP与面S5在最右侧的交点。
通过计算可以分别得到nS1和nx之间的夹角θ1,nS3和nx之间的夹角θ2,nS4和nx之间的夹角θ3,nS6和nx之间的夹角θ4。根据θ1和θ2,θ3和θ4之间的关系,可以得到此种情况下射线与三角形之间的交点统计方法为:①θ1和θ2同时为锐角或钝角,记射线与CAD模型在此处有1个交点;②θ3和θ4分别为锐角和钝角时,无交点。
特别地,CAD模型的STL格式中可能存在几个面与射线同时共面的情况,在交点统计时,只关注最左和最右端的两个面的法向量与射线的夹角之间的关系即可,上述射线与三角形共面时的交点统计方法仍适用。
1.3 单元识别与局部细化
以带孔立方体结构为例,由CAD模型向固定网格中有限元分析模型的转换过程如图8所示。
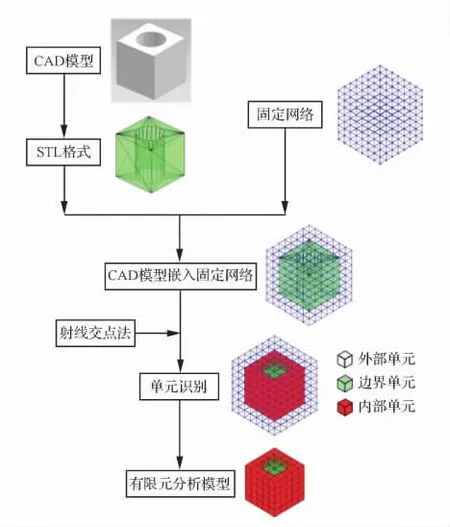
图8 CAD模型向固定网格中分析模型的转换流程Fig.8 Transform flow from CAD model to analysis model at fixed grid
在笛卡尔坐标系中,首先建立一个尺寸略大于结构CAD模型的六面体,并采用各向等比的方法将其划分成规则的网格结构;然后将STL格式的CAD模型嵌入网格结构中;接着根据1.2节阐述的射线交点法判断固定网格中每一个节点与CAD模型的位置关系,进而确定单元的属性,完成CAD模型向固定网格中有限元分析模型的转换。相对于当前固定网格中主要采用的2种模型转换方法而言,本文所提方法避免了采用隐式函数描述CAD模型方法中将CAD模型人为地分解成若干基元,再通过布尔运算进行组合的过程;避免了采用像素模型描述CAD模型方法中需借助专门工具生成像素模型的过程,不需要任何的预先处理,直接根据CAD模型的信息得到其在固定网格中对应的分析模型。
为提高固定网格中有限元分析模型对CAD模型的近似精度,采用八叉树技术对边界单元进行细化处理,并对细化后的子单元进行新的单元识别,如图9所示。
一般而言,固定网格越密,对边界单元的细化层级越多,有限元分析模型越接近CAD模型,但所耗费的时间也越长。以带孔立方体为例,固定网格中单元数量与CPU耗时之间的关系如图10所示。由图10可知,网格越密,转换模型所耗费的时间也越多。因此需要在模型近似精度和计算效率上进行合理的平衡。
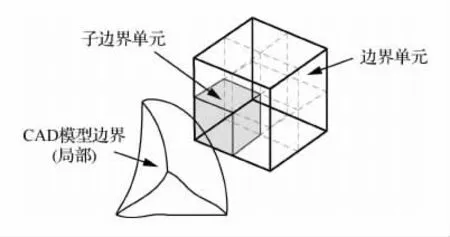
图9 基于八叉树技术的边界单元细化Fig.9 Refinement of boundary element based on octree technique

图10 固定网格数量与CPU耗时之间的关系Fig.10 Relationship between number of fixed grids and CPU times
2 加权B样条有限胞元方法
2.1 B样条有限胞元方法
B样条有 限胞元方法 (B-Spline Finite Cell Method,BSFCM)[3-6,24-25]作为计算力学领域中新兴的先进数值方法之一,其本质是一种采用高阶连续的B样条基函数作为待求物理场的插值函数,并使用四叉树/八叉树自适应积分策略处理被结构边界所分割的网格单元的虚拟区域法。
为求解结构Ωphy上的线弹性力学问题,虚拟区域法先将结构Ωphy嵌入到规则的计算域Ω中(如图11所示),然后采用固定网格离散Ω,并基于变分原理建立离散后的平衡方程组,最后求解此方程组得到结构的待求物理场。
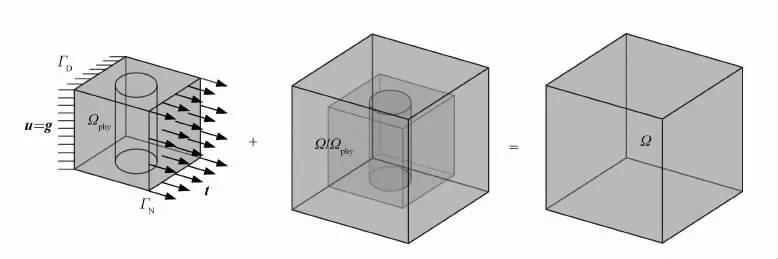
图11 结构域Ωphy扩展到简单规则的计算域ΩFig.11 Embedded domainΩextendedfrom structural domainΩphy
定义在计算域Ω上的线弹性问题为
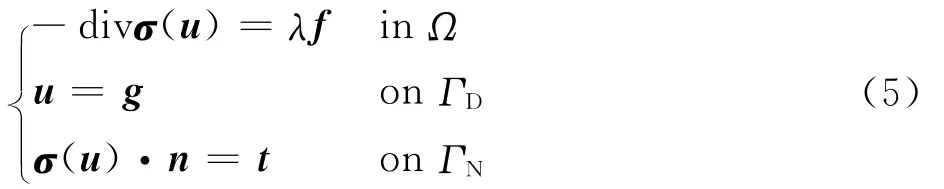
式中:σ为柯西应力张量;u为位移向量;g为边界ΓD上的给定位移;f为体积力向量;t和n分别为边界ΓN上的外界力和单位外法向量。标量因子λ定义为

相容方程及本构方程描述为
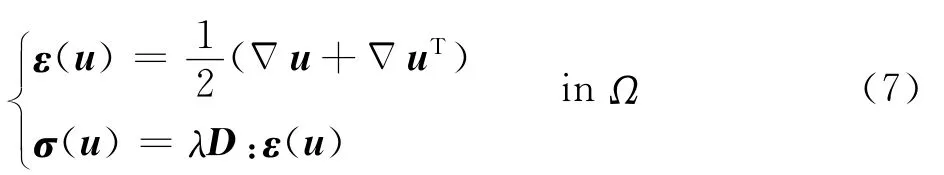
式中:ε为应变张量;D为Ωphy上的弹性本构张量。
定义以下2个可容位移场空间
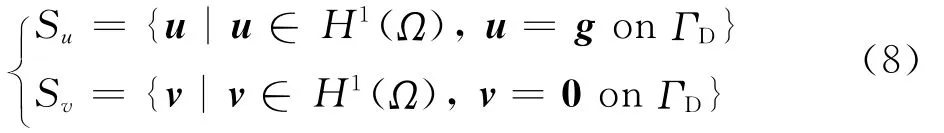
式中:H1(Ω)代表一阶希尔伯特空间。对于嵌入域Ω,式(5)的等效积分弱形式可以表示为
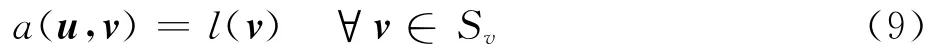
式中:

假定Shu是Su的有限维子空间,Shv是Sv的有限维子空间,因此上述问题的离散问题为寻找一个离散的解uh∈Shu,使其能够满足
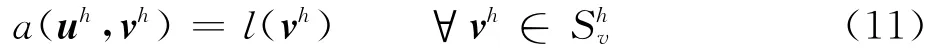
类似于有限单元法,计算域Ω可以离散成独立于结构域Ωphy的规则的网格单元(这些单元在BSFCM中也称为“胞元”),根据文章第1节所述的方法,可以将这些单元区分为内部单元、边界单元和外部单元。在BSFCM中,利用定义在固定网格上的高阶B样条形函数来离散插值位移向量uh和vh。对于三维问题,三变量B样条基函数可以表示为

式中:Ni,p(ξ)、Nj,q(η)和 Nh,r(γ)分别是p、q和r次单变量B样条基函数,分别定义在参数域坐标系下 的 Ξ = {ξ1,ξ2,…,ξns+p+1},H = {η1,η2,…,ηms+q+1}和ψ = {γ1,γ2,…,γks+r+1}节点矢量上,他们的个数分别为ns、ms和ks。对于计算域Ω内的任意一点P = [x,y,z]T,可由以下的映射关系确定
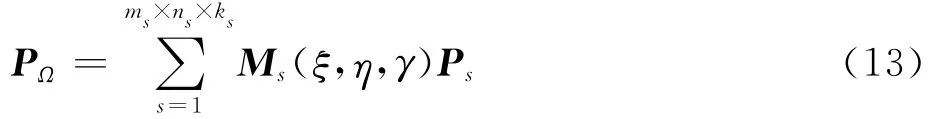
式中:Ps= [xs,ys,zs]T表示三维空间中的第s个控制点。计算域Ω内的点PΩ,可由以下简单的线性映射确定
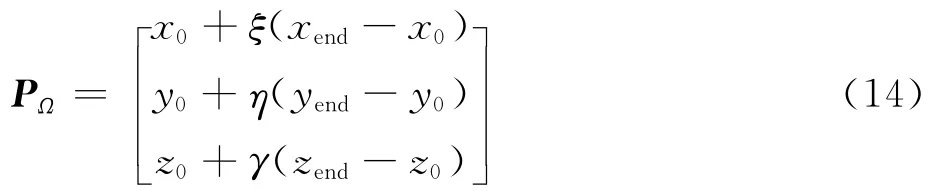
式中:x0和xend分别为计算域在x方向上的最小和最大值;y0和yend分别为计算域在y方向上的最小和最大值;z0和zend分别为计算域在z方向上的最小和最大值。
本文中采用统一开放的节点矢量来定义B样条基函数[26],根据考克斯-德布尔递推公式,定义在Ξ上的第i个p次B样条基函数Ni,p(ξ)的表达式为
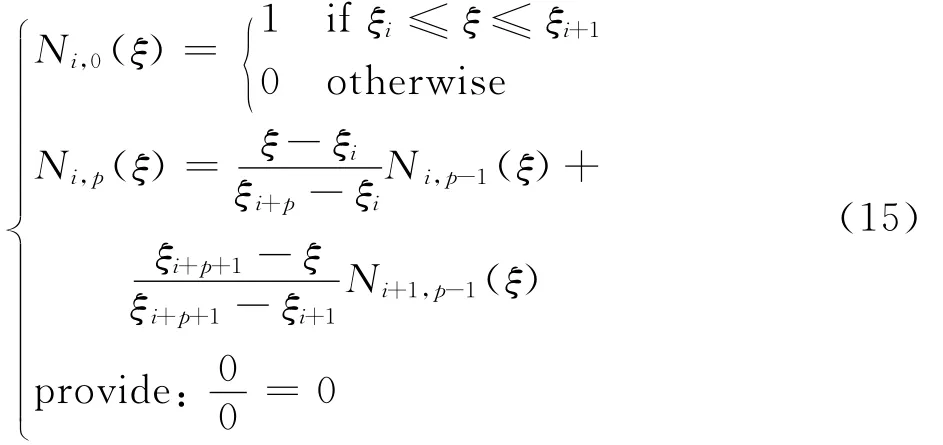
由式(8)可知,对于vh而言,基函数Ms在边界ΓD上的值需为0,则存在一组向量A,使得vh满足线性插值形式

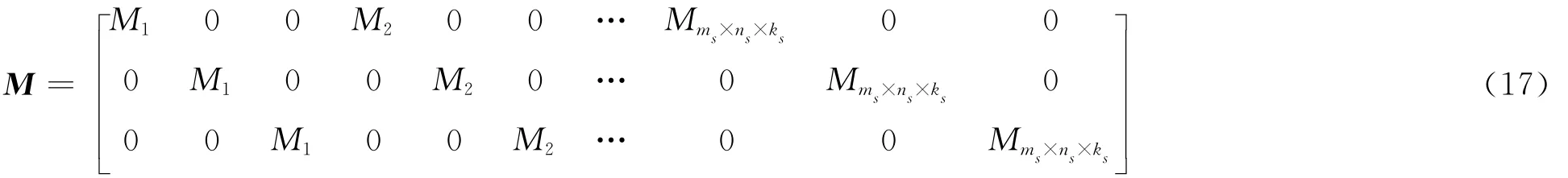
假设U是一组待求位移向量,表示控制点Ps的位移。对于给定的函数gh∈Sh,如果满足gh|ΓD=g,则位移的离散形式可以表示为

特别地,对于施加齐次Dirichlet边界条件的情况,g=0。根据Riz-Galerkin方法,将式(16)和式(18)代入式(11),可得到BSFCM 中的刚度方程

式中:K是整体刚度矩阵;F是整体载荷矩阵;具体为

式中所表达的总体刚度矩阵K和总体载荷矩阵F在BSFCM中均由单元的刚度矩阵和载荷向量组装而成。根据第1节所确定的单元属性不同,其刚度矩阵计算的方法也不同。对于外部单元,由于其对K和F没有贡献,因此无需计算;对于内部单元,直接按照传统有限元方法的单元积分方式进行计算;对于边界单元,根据1.3节的细化策略,采用自适应积分方法沿着CAD模型边界加密高斯积分点,对边界单元中的有材料部分进行高精度的积分计算。
式(20)中,B是应变位移矩阵(几何矩阵),表达式为

2.2 Dirichlet边界条件施加
不失一般性,本文仅考虑BSFCM框架下齐次Dirichlet边界条件的精确施加策略,并选择了简单且能精确施加齐次Dirichlet边界条件的加权B样条方法[27-28]。该方法的本质就是将B样条基函数Ms在齐次位移约束边界ΓD上的值修正为0,修正后的式(18)变为

式中:权函数ω(x,y,z)是隐式函数,且满足ω(x,y,z)|ΓD=0。对于实际CAD模型的约束边界,可以构造其隐式函数表达式,并将其直接作为权函数。
在使用权函数ω(x,y,z)修正B样条基函数M之后,式(21)定义的几何矩阵B也相应地变化为

此外,在求解一些对称问题时,常对结构的1/2、1/4或1/8结构模型进行力学分析。此时的位移边界条件需施加在对称边界上,如:在边界ΓDX上要求x方向的位移为0,在边界ΓDY上要求y方向的位移为0,在边界ΓDZ上要求z方向的位移为0,也即分别构造在ΓDX上的权函数ωx=0,在ΓDY上的权函数ωy=0和在ΓDZ上的权函数ωz=0。因此,基函数矩阵变化为

3 CAD模型分析流程
综合本文第2节和第3节的内容,可以建立一种由结构CAD模型至固定网格仿真分析的设计框架,如图12所示。

图12 固定网格中CAD模型分析流程Fig.12 Analytic flow of CAD model in fixed grid
首先通过设计软件建立结构的CAD模型,并将其保存成采用边界形式表示的STL格式;然后将CAD模型嵌入建好的固定网格中,并采用射线交点法进行单元识别,同时对识别出的边界胞元采用八叉树技术进行细化,以提高有限元分析模型的建模精度;再者对固定网格区域采用BSFCM,并通过加权B样条方法施加Dirichlet边界条件和载荷;最后求解获得CAD模型的有限元仿真结果。
4 数值算例
4.1 平板带孔结构
平板带孔结构作为计算力学中的经典算例,相关学者对此进行了深入的研究[8]。不失一般性,本文选用线弹性平板带孔结构算例来说明文中建立的基于边界描述的CAD模型快速分析方法的有效性。假定其杨氏模量和泊松比分别为2.074×105MPa和0.3。如图13所示,平板带孔结构沿±z向承受的均布载荷为t1=22.5MPa,沿±y向承受的均布载荷为t2=45MPa。为提高计算效率,将平板带孔结构简化为1/8模型进行分析,简化后模型的尺寸为R=1mm,L=4mm,H=0.5mm。
简化后的平板带孔结构模型的STL格式如图14所示。
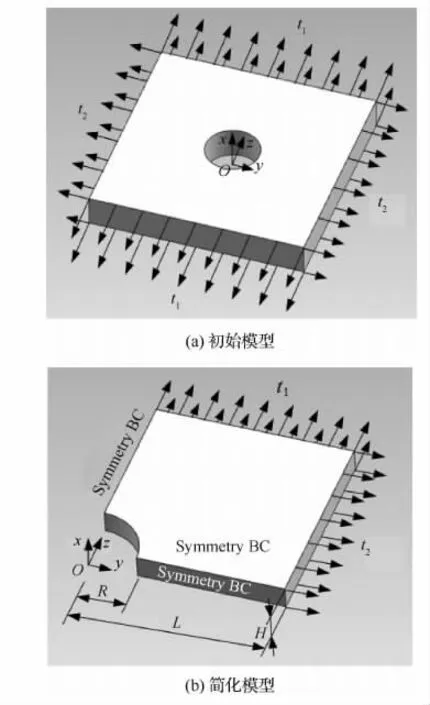
图13 均布载荷作用下的平板带孔结构Fig.13 Plate with a circular hole under uniform loads

图14 平板带孔结构简化模型的STL格式Fig.14 STL format of simplified model for plate with a circular hole
根据平板带孔结构的特点,建立一个尺寸略大于平板带孔结构且分辨率为8×8×2的固定网格,然后将平板带孔结构嵌入固定网格中,并应用射线交点法进行单元属性识别,建立固定网格中的有限元分析模型,如图15所示。
为提高固定网格中有限元分析模型的精度,采用八叉树技术对边界单元进行分层细化,然后在固定网格中应用BSFCM,并通过加权B样条方法施加齐次Dirichlet边界条件和载荷,可以得到平板带孔结构的应力云图如图16所示。由图16可知,最大应力发生在孔的上边缘处,且最大应力值约为133.04MPa。
当网格单元数量较少时,网格单元数量不同所得到的最大应力也不同,但当网格单元数量满足一定的值时,最大应力趋于稳定,如图17所示。图17中网格单元数量从16(4×4×1)~4 096(32×32×4)的变化过程中,当网格数量超过128(8×8×2)时,平板带孔结构的最大应力逐渐收敛。
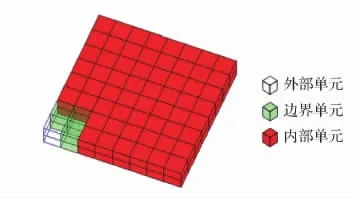
图15 平板带孔结构在固定网格中的分析模型Fig.15 Analytic model for plate with a circular hole in fixed grid
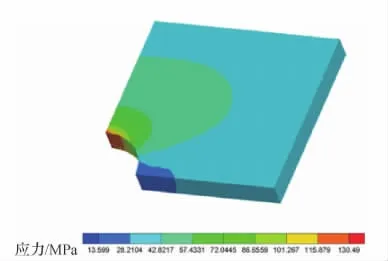
图16 固定网格中平板带孔结构的应力云图Fig.16 Contour of Von-Mises stress of plate with a circular hole in fixed grid
作为参考,当采用传统有限元方法求解上述平板带孔结构的应力分布时,使用线弹性四面体网格或六面体网格离散结构区域,获得的单元数量为2 637个,如图18所示。平板带孔结构的应力云图如图19所示,最大应力发生在孔的上边缘处,最大应力值约为130.49MPa。在传统有限元方法中,最大应力随网格数量的变化曲线如图20所示。

图17 固定网格中不同网格数量下的最大应力Fig.17 Maximum Von-Mises stress with different elements in fixed grid

图18 平板带孔结构在传统有限元方法中的分析模型Fig.18 Analytic model for plate with a circular hole in classical finite element method
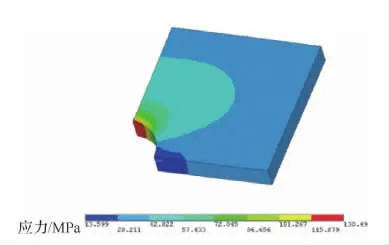
图19 传统有限元方法中平板带孔结构的应力云图Fig.19 Contour of Von-Mises stress of plate with a circalarhole obtained by classical finite element method

图20 传统有限元方法中不同网格数量下的最大应力Fig.20 Maximum Von-Mises stress with different elements in classical finite element method
对比本文方法和传统有限元方法可知,本文方法可以实现平板带孔结构CAD模型至固定网格中分析模型的直接快速转换,并且通过较少的单元即可获得与传统有限元方法同等精度的计算结果。由图16和图19可知,2种方法获得的应力云图基本一致,最大应力的相对误差约为2.2%。
4.2 连接结构
为了进一步说明本文所提方法的有效性,下面通过一个更复杂的例子——航空连接结构进行验证。连接结构的CAD模型及其载荷和约束情况如图21所示。
连接结构的主要尺寸为:L11=80mm,H11=80mm,H12=20mm,H13=20mm,R11=5mm,R12=10mm。连接结构所承受的载荷为集中力,位于连接结构左端孔中心处,其值为Fzz=5000N。连接结构的约束条件为其右端两个孔的位移约束。同时假定连接结构的杨氏模量和泊松比分别为2.074×105MPa和0.3。
连接结构CAD模型的STL格式如图22所示。建立一个尺寸略大于连接结构且分辨率为25×60×50的固定网格,然后将连接结构嵌入固定网格中,并应用射线交点法进行单元属性识别,建立固定网格中的分析模型,如图23所示。
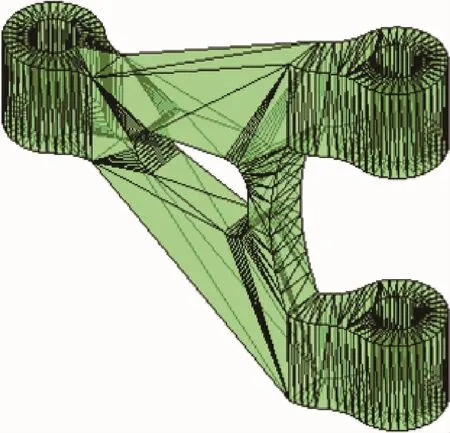
图22 连接结构的STL格式Fig.22 STL format of connector structure
对边界单元采用八叉树进行分层细化,提高分析模型对CAD模型的近似精度。然后在固定网格中应用BSFCM,并通过加权B样条方法施加Dirichlet边界条件和载荷,可以得到连接结构的应力云图如图24(a)所示。由图24(a)可知,最大应力发生在连接结构左端过渡处,且最大应力值约为222.16MPa。采用传统有限元方法计算得到连接结构的应力云图如图24(b)所示。由图24(b)可知,最大应力同样发生在连接结构的左端过渡处,且最大应力值约为219.02MPa。由图24可知,2种方法所得的应力云图基本一致,最大应力相对误差约为1.5%。

图23 连接结构在固定网格中的分析模型Fig.23 Analytic model for connector in fixed grid

图24 连接结构应力云图Fig.24 Contour of Von-Mises stress of connector
5 结 论
本文研究了复杂结构在固定网格中的力学分析问题,提出了一种基于CAD模型边界表示的结构模型至固定网格中分析模型的快速转换方法,在保证模型转换精度的同时,提高了模型转换的效率、降低了模型转换的复杂度。同时结合计算力学领域新兴的加权B样条有限胞元方法,建立一种固定网格中结构CAD模型的快速分析框架,实现了结构CAD设计与分析的有效集成,为结构设计与分析的一体化建设提供了一种思路。

