复合式旋翼飞行器多目标控制分配策略

郑峰婴＊，刘龙武程月华陈志明成锋娜

1.南京航空航天大学 航天学院，南京 2100162.南京林业大学 机械电子工程学院，南京 210037

复合式旋翼飞行器因同时具有推力装置、固定翼和旋翼，既能实现直升机飞行模式的垂直起降、悬停飞行，又具备固定翼飞机高速度、远航程和长航时飞行能力，近年来备受世界各国直升机研究机构及研究人员的关注，是旋翼类飞行器研究的热点。如：美国西科斯基飞机公司研制的X2试验样机［1］，欧洲空客公司制造的X3复合式直升机［2］，均结合直升机和固定翼飞机的优势，既提高巡航速度，又保证低速机动性。

与常规旋翼飞行器相比，复合式旋翼飞行器结构独特、气动特性更加复杂、飞行模式增多。在飞行过程中存在模式切换，悬停和低速飞行时，主要采用直升机模式飞行；在中速飞行时，直升机模式和固定翼飞行器模式同时参与；在高速飞行时，主要采用固定翼飞行器模式。复杂多变的工作模式为复合式旋翼飞行器控制系统的设计带来了较大的难度，如何设计切实可行的模式切换控制策略，有效处理操纵量控制受限、交叉强耦合及非线性特性，解决模式切换时的操纵冗余，实现过渡阶段的稳定控制，减轻飞行控制系统的设计难度，是复合旋翼飞行器控制亟待解决的关键问题。

目前，尽管美国等技术先进强国已研发出先进的复合高速直升机，但也尚处于起步阶段，由于技术保密等原因，此领域公开发表的文献较少。国内对复合式旋翼飞行器的研究主要集中在飞行器总体参数设计，空气动力学及其气动干扰如旋翼与机翼、旋翼与旋翼、旋翼与机体等，旋翼动力学及其飞行特性等方面［3－4］，复合式旋翼飞行器的飞行控制技术涉及甚少。从已发表的公开资料来看，复合式旋翼飞行器的控制技术相关研究都只针对特定的小型旋翼飞行器且局限于某一特定的飞行状态，如高速飞行［5］、悬停［6］等，尚未涉及模式切换的控制。

多操纵量飞行器控制分配的研究成果可为复合式旋翼飞行器多模式切换的控制策略提供较为理想的理论支撑。控制分配方法使得飞行控制律分成两个相对独立的模块：一是基本控制律模块；二是控制分配模块。当飞行器出现模式切换时，可以利用控制分配模块实现模式过渡控制，不需要重新调整复杂的飞行控制律，以此降低传统模式切换技术的设计难度。

控制分配的模式切换方法从分配原理上可分为线性和非线性两类分配方法。线性分配方法主要包括伪逆法［7］、链式分配法、直接分配法［8］、线性规划法［9］等；非线性分配方法主要包括截距修正法［10］、分段线性规划法［11］、非线性规划法［12］、智能控制分配法［13］等。国内外学者对于控制分配技术的理论研究和工程应用已取得较多成果。如：Cristofaro等［13］提出一种基于非线性观测器的控制分配技术，用于解决仿射非线性系统的容错控制问题；Pedro和Tshabalala［14］提出了基于遗传算法的控制分配方法用于某固定翼无人机（UAV）的容错控制；Hamayun和Edwards［15］结合积分滑模控制器和控制分配，可对控制信号进行重新分配，避免了对控制器重新设计的繁琐。路瑶等［16］在飞行器多目标控制分配方面，Buffington［17］将控制面偏转量最小作为约束优化控制分配目标，用于解决某无尾战斗机部分执行机构饱和问题；杨恩泉等［18］通过给出多目标非线性控制分配解的评价指标及评价方法，提出了一种解决多目标非线性规划的控制分配方案，实现飞行器不同飞行条件和任务下对多种目标的综合权衡分配。贾瑞和吴梅［19］提出基于寻优算法的动态控制分配方案，用于复杂多操纵舵面的多目标控制系统；Chollom等［20］应用粒子群算法调整加权矩阵以获得状态反馈控制增量，优化无人机横向运动轨迹跟踪能力；Lee等［21］提出了一种基于参数优化的倾转无人机自动驾驶系统，解决了倾转无人机的非线性、不确定性及众多设计条件和操纵条件限制性问题，保证了倾转无人机飞行过程具有良好的稳定性。

综上可见，研究复合式旋翼飞行器模式切换的控制策略时，可以借鉴其他飞行器舵面控制分配的方法，但还需要重点解决以下几个问题：①多目标控制分配技术中处理舵面动态特性的研究较少，没有综合考虑飞行器操纵量存在的强耦合、非线性、舵面受限等问题；② 针对复合式旋翼飞行器多控制通道及多目标性能函数，如何设计合适的通道权重系数和多目标赋权系数是提高模式切换控制效能的关键；③应用于实际系统时，模式切换控制的快速性、稳定性和鲁棒性仍是难点问题。此外，建立完整的复合式旋翼飞行器模型以用于模式切换控制能力的分析亦是需要解决的问题。

由此，本文提出一种基于赋权多目标混合优化的控制分配策略，选取控制指令跟踪误差最小，操纵量偏转量最小，操纵效率最高作为控制分配性能指标，设计带约束的赋权性能指标评价函数，有效处理操纵量控制受限、交叉强耦合及非线性特性。通过动态改变操纵量及控制通道的权重系数，充分发挥各操纵舵面效能。同时改进粒子群寻优算法对控制信号实时重分配，以此提高计算速度，快速求解操纵变量。最终实现飞行器不同模式的平稳快速切换，保证系统的安全性。

1 复合式旋翼飞行器动力学模型

复合式旋翼飞行器由于增加了固定翼和推力装置，结构更加复杂，各部件间存在强烈的气动干扰，具有高度非线性、强耦合、操纵舵面受限等特点，加大建模难度。此外，其飞行动力学特性与飞行模式密切相关，多变的飞行模式增加了建模的复杂性。

由于技术保密等原因，现役复合式旋翼飞行器基本无公开详细气动数据。本项目拟参考国外X-49、UH-60等典型旋翼飞行器的结构布局及部分建模数据，研究近似X-49的全量非线性模型，本文所研究的复合式旋翼飞行器外形结构如图1所示，采用分体建模方法，将飞行器分为旋翼、机翼、机身和涵道风扇4个模块，分别进行气动力模型分析，同时，考虑到机身和机翼的复杂结构，采用风洞试验数据进行拟合［22］，提高气动模型的可靠性。

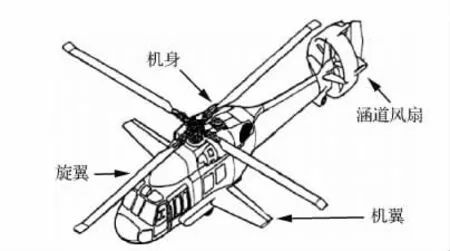
图1 复合式旋翼飞行器模型Fig.1 Model for compound rotorcraft

1.1 旋翼气动力模型

建立旋翼挥舞运动方程、旋翼诱导速度公式和旋翼气动力方程求解旋翼气动力模型。首先，由旋翼受力分析可知，所有力矩对挥舞绞的合力矩为零，即

式中：MG、MC、MF和 MT分别为重力、离心力、挥舞惯性力和升力对挥舞绞的力矩。

由力矩平衡方程可得旋翼挥舞运动微分方程为

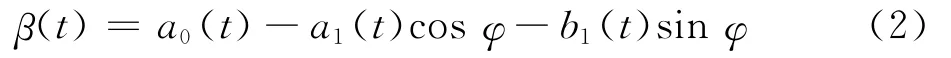
式中：β为挥舞角；a0为旋翼锥度角；a1为旋翼锥体后倒角；b1为旋翼锥体侧倒角；φ为方位角，并采用桨盘平面法可得到旋翼二阶挥舞运动方程［23］。

随后，依据叶素理论，在桨毂坐标系下，积分可以得到旋翼的拉力、后向力和侧向力，以及滚转、俯仰和偏航力矩［24］，再通过坐标变换即可得到旋翼在机体坐标系下的力和力矩为

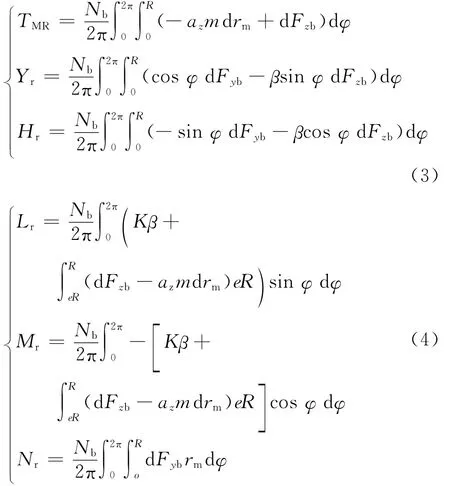
式中：TMR、Yr、Hr分别为旋翼的拉力、后向力和侧向力；Lr、Mr、Nr分别为旋翼产生的滚转、俯仰和偏航力矩；Nb为旋翼的桨叶片数；m为叶素微元的质量；az为桨叶剖面加速度的法向分量；Fzb、Fyb分别为叶素微元的垂向力和后向力；R为旋翼半径；rm为旋翼半径微元量；K为旋翼刚度系数；e为无刚量的等效挥舞铰偏置量。

依据动量理论可得旋翼诱导速度为

式中：Ω为旋翼转速；μ为桨叶前进比。

由诱导速度可得旋翼入流比与旋翼升力系数的关系为

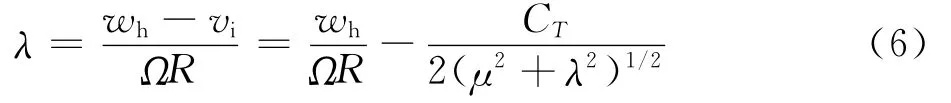
式中：wh表示桨毂速度在本体系下Obzb轴方向的分量。

旋翼拉力系数为

式中：ρ为空气密度；A为旋翼桨盘面积。

1.2 机翼气动力模型

由风洞试验数据拟合得到风轴系下的机翼气动力和力矩系数为［24］

式中：CL、CD、Cm分别为机翼升力系数、机翼阻力系数和机翼气动俯仰力矩系数；αw、θw分别为机翼迎角和桨距角。

机翼动压定义为

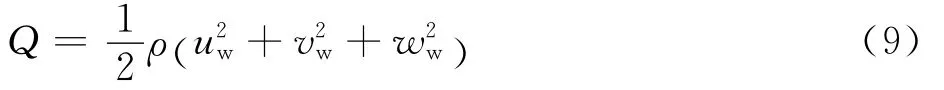
式中：uw、vw、ww分别为复合式旋翼飞行器风轴系的前飞速度、偏航速度和升降速度。

则风轴系下所受的气动力和力矩为

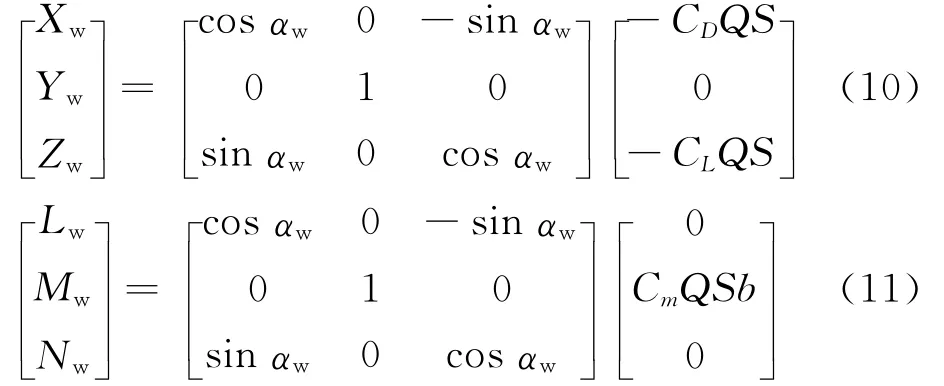
式中：Xw、Yw、Zw分别为风轴系下机翼产生的纵向、横向和轴向气动力；Lw、Mw、Nw分别为风轴系下机翼产生的滚转力矩、俯仰力矩和偏航力矩；S为稳定面面积；b为机翼展长。

1.3 机身气动力模型

假设复合式旋翼飞行器的纵向运动所受力和力矩系数与迎角和侧滑角相关，而对于横向运动，仅与侧滑角相关，且忽略角速率和旋翼尾流，求取机身动压和侧滑角为

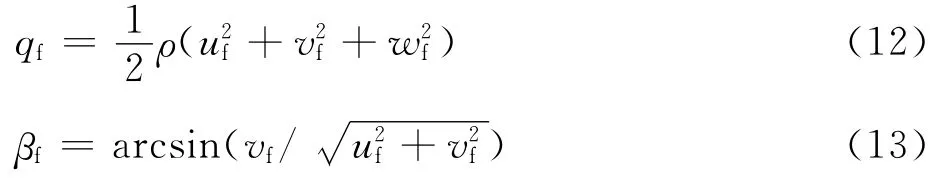
式中：qf为机身动压；βf为机身侧滑角；uf、vf、wf分别为复合式旋翼飞行器机身轴系下的前飞速度、偏航速度和升降速度。

并依据机身气动力和力矩系数、机身动压和侧滑角，可得风轴系下机身力和力矩为

式中：Xf、Yf、Zf分别为风轴系下机身产生的纵向、横向和轴向气动力；Lf、Mf、Nf分别为风轴系下机身产生的滚转力矩、俯仰力矩和偏航力矩；Af为机身最大迎风面积；Lfs为机身长度；CDf、CSf、CLf与Cmf，x、Cmf，y、Cmf，z分别为风轴系下机身气动力和力矩系数，可根据风洞试验数据拟合得到［23］。

1.4 涵道风扇气动力模型

忽略涵道风扇自身的侧向力和后向力，仅考虑涵道风扇所产生的推力，且推力方向可在三维空间作二自由度小角度变化，通过对涵道风扇推力矢量受力分析，得到涵道风扇在本体系下的力和力矩分别为

式中：XT、YT、ZT分别为涵道风扇产生的推力在本体系下3个坐标轴方向的分量；LT、MT、NT分别为涵道风扇产生的力矩在本体系3个坐标轴方向的分量；STA为机身轴系下纵向距离；T为涵道风扇所产生的推力；θ1为涵道风扇产生推力与纵对称面夹角；θ2为涵道风扇产生推力在纵对称面内投影与x轴夹角。

将上述各部件所得气动力和力矩转换到机体坐标系中，并将重力G沿机体坐标系分解，相加后可得复合式旋翼飞行器的合气动力和合力矩，并依据机械运动规律，可得复合式旋翼飞行器的动力学方程为［24－25］

式中：g为重力加速度；u、v、w分别为复合式旋翼飞行器本体系下的前飞速度、偏航速度和升降速度；φ、θ、ψ分别为复合式旋翼飞行器俯仰角、偏航角和滚转角；p、q、r分别为俯仰角速度、偏航角速度和滚转角速度；Xtot、Ytot、Ztot分别为旋翼、机翼、机身和涵道风扇的在本体坐标系下坐标轴正方向的合力；Ltot、Mtot、Ntot分别为旋翼、机翼、机身和涵道风扇的在本体系下坐标轴方向的合力矩；Ix、Iy、Iz分别为复合式旋翼飞行器对本体系x轴、y轴、z轴的转动惯量；Ixz、Ixy分别为本体系下对应两坐标轴的惯性积。

2 基于赋权系数的混合多目标控制分配策略

2.1 操纵舵面特性分析

相比于常规旋翼飞行器，复合式旋翼飞行器增加了固定机翼和涵道风扇，因而操纵量增加，不同模式下（直升机飞行模式和固定飞行模式）的操纵舵面是不一样的，具体的分配情况如表1所示。当悬停或低速飞行时（直升机飞行模式，速度小于40m／s），固定机翼将不能够提供飞行所需的升力或提供的升力较小，可以忽略不计，同时涵道风扇也不需要提供推力，此时升力和推力主要由旋翼提供；当复合式旋翼飞行速度较高时（定翼飞行模式，速度大于70m／s），与之相反，旋翼由于桨叶失速等原因提供的升力和推力较小，升力和推力将主要分别由固定机翼和涵道风扇提供；当两种飞行模式进行切换时，各个操纵量均作用于复合式旋翼飞行器，控制情况较为复杂。

图2给出了复合式旋翼飞行器在不同模式下作定常直线飞行时，各操纵量对姿态响应随前飞速度的变化曲线。其中，图中阴影部分表示过渡模式的变化曲线。旋翼操纵量与前飞速度的变化曲线表明，旋翼总距φ7、横向周期变距A1s和纵向周期变距B1s随前飞速度的增大而逐渐减小，且当前飞速度达到70m／s以上时，A1s、B1s趋近于零，而φ7的值趋近于最小值；而襟副翼操纵量与前飞速度变化曲线、涵道风扇推力与前飞速度变化曲线表明，右襟副翼偏角θwr、左襟副翼偏角θwl和涵道风扇推力T随前飞速度的增大而增加，当速度较小时，θwr、θwl、T 数值较小，可忽略不计；涵道风扇推力夹角随前飞速度变化曲线表明，本体坐标系下X轴与涵道风扇所产生的推力在纵对称面内的投影之间的夹角θ2随速度的增大而变小，纵对称面与涵道风扇所产生的推力之间的夹角θ1随速度的增加而增加。而过渡模式下的变化曲线表明，各操纵量在此区间取值较大，均不可忽略。

表1 复合式旋翼飞行器操纵量在各飞行模式下的分配情况Table 1 Distribution of maneuvering variables of compound rotorcraft in each flight mode

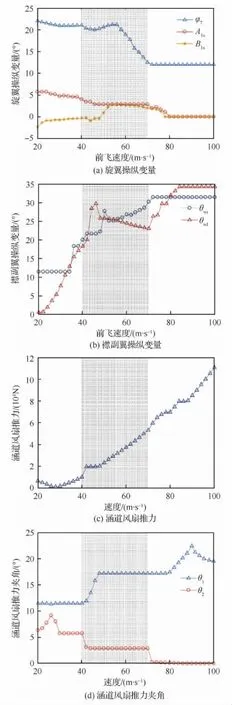
图2 操纵量随前飞速度变化曲线Fig.2 Variation of manipulated variable with forward flying speed

由上述操纵舵面特性分析可知，当复合式旋翼飞行器过渡模式飞行时，各个舵面均对复合式旋翼飞行器发挥一定的效能，此时操纵量包括：旋翼总距φ7、横向周期变距A1s、纵向周期变距B1s、右襟副翼偏角θwr、左襟副翼偏角θwl、涵道风扇推力T、纵对称面与涵道风扇所产生的推力之间的夹角θ1和本体坐标系下X轴与涵道风扇所产生的推力在纵对称面内的投影之间的夹角θ2；而复合式旋翼飞行器实际控制系统中虚拟控制指令通常为姿态角或速度变量，即虚拟指令为3维变量，操纵量维数大于虚拟控制指令维数，存在操纵冗余。

2.2 控制分配策略设计

设定复合式旋翼飞行器实际操纵量，复合式旋翼飞行器模式切换时操纵冗余问题可表示为

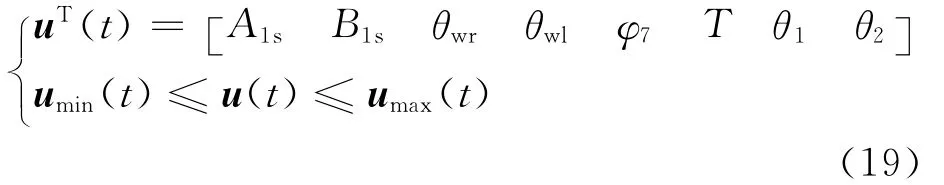
式中：umin（t）为8个操纵量边界最小值；umax（t）为8个操纵量边界最大值。

复合式旋翼飞行器虚拟控制指令为

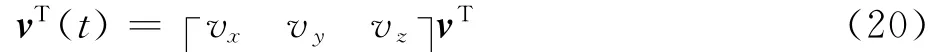
复合式旋翼飞行器操纵冗余问题求解即能够找到vT（t）→uT（t）的非线性映射g（·），使得u（t）＝g（v（t）），且满足umin（t）≤u（t）≤umax（t）。

在实际控制系统设计时，虚拟控制指令与操纵量的数值关系可通过对复合式旋翼飞行器动力学配平和线性化求得，即

式中：B为控制分配效率矩阵，即

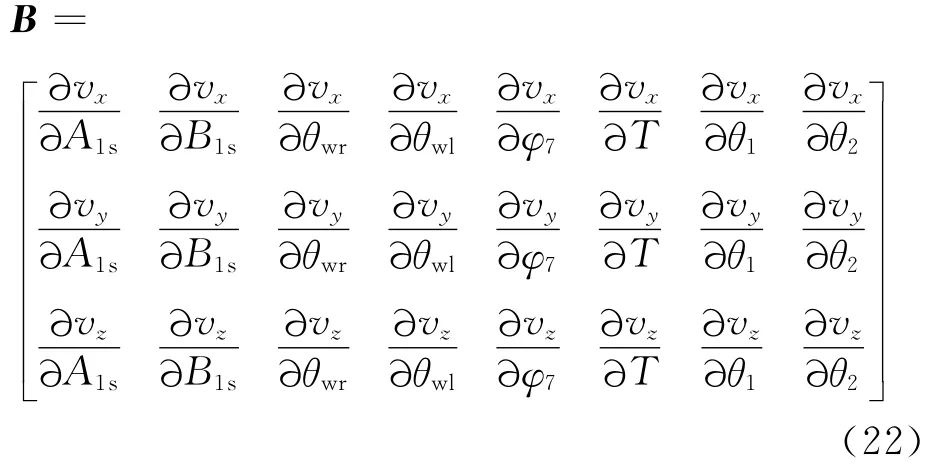
由式（22）可知，复合式旋翼飞行器每个操纵量都与3个通道的虚拟控制指令密切相关，各个通道的操纵量相互影响，即各控制操纵量都与控制分配效率矩阵B相关，这将增加控制分配策略的设计难度。此外，由于控制分配效率矩阵B为奇异矩阵，且由于操纵量边界约束，不可直接求取实际的控制变量。

本文综合考虑复合式旋翼飞行器操纵量边界约束条件和模型非线性化等式约束条件，飞行器模式切换过渡过程中指令跟踪控制能力及操纵控制效率，提出复合式旋翼飞行器多目标控制分配策略，可表述为

式中：Wu＝diag（wu1，wu2，…，wu8），wu1，wu2，…，wu8分别为复合式旋翼飞行器8个操纵量所对应的权重系数；Wv＝ diag（wv1，wv2，wv3），wv1、wv2和wv3分别为俯仰、偏航和滚转通道所对应的权重系数；n为复合式旋翼飞行器性能指标的个数；fi为复合式旋翼飞行器控制分配性能指标评价函数。

定义（Pareto最优解） 针对式（23）混合优化问题，若-x＊＝［u＊v＊Wv＊Wu＊］，x＊满足v＊（t）＝Bu＊（t），umin（t）≤u＊（t）≤umax（t），使 得 x ＝［u v WvWu］，fi（x＊）≤ fi（x）（i＝ 1，2，…，n），且-fi（x＊）＜fi（x），则x＊＝ ［u＊v＊Wv＊Wu＊］为式（23）的 Pareto 最 优 解［26］，其 中，x ＝［u v WvWu］满足v（t）＝Bu（t），umin（t）≤u（t）≤umax（t）。

定理1 若选取复合式旋翼飞行器指令跟踪误差最小作为飞行任务评价性能指标，性能指标函数可设计为

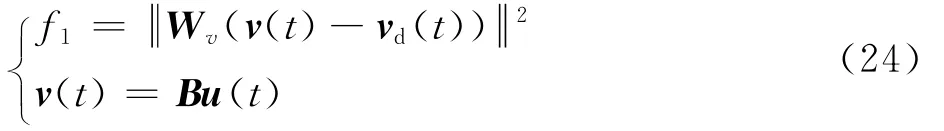
假设权系数矩阵Wu、Wv已知，则操纵量Pareto最优值为

式中：vd（t）为期望虚拟控制指令。

证明 当Wvv（t）＝Wvvd（t）时，f1取值最小，且v（t）＝Bu（t），故WvBu（t）＝Wvvd（t）时，f1取值最小，进一步，由于B为奇异矩阵，无法直接求得逆矩阵，故可对WvBu（t）＝Wvvd（t）两边同时乘矩阵 （WvB）T，可得

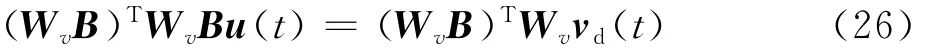
取G1＝ （WvB）TWvB ，并对式（26）两边同时乘G1的逆矩阵，即可证明定理1。

定理2 若选取复合式旋翼飞行器操纵量偏转量最小作为性能评价指标，对应的操纵量偏转误差性能指标评价函数可表示为

则操纵量Pareto最优值为

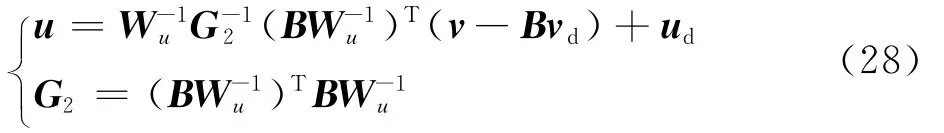
式中：ud（t）为期望操纵量，可通过复合式旋翼飞行器动力学配平和线性化计算得到。

证明 取e2（t）＝Wu（u（t）－ud（t）），且v（t）＝Bu（t），则可知

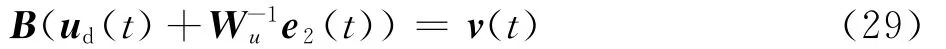
化简式（29）可得

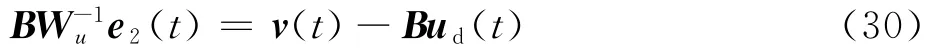
由于B为奇异矩阵，故对式（30）两边同时乘（BW－1u）T，可得

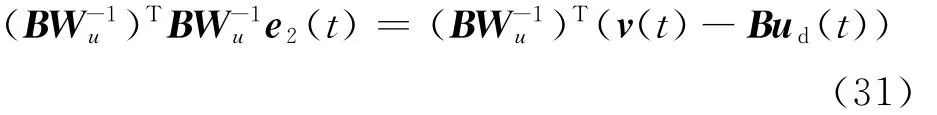
取G2＝ （BW－1u）TBW－1u，并对式（31）两边同时乘以G2的逆矩阵，则

对式（32）两边同时乘以Wu的逆矩阵，并移项后可得

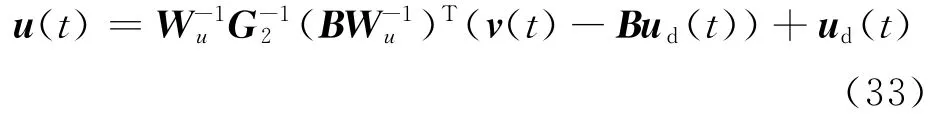
即定理2得证。

定理3 若复合式旋翼飞行器同时以指令跟踪误差和操纵量偏转量最小作为性能指标，性能指标评价函数可表示为

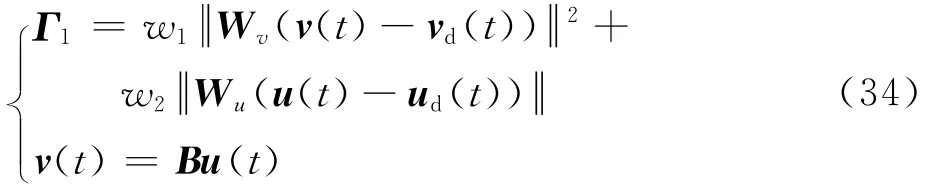
则操纵量Pareto最优值为

式中：w1、w2分别为指令跟踪误差性能指标和操纵量偏转量性能指标所对应的权重系数。

证明 将式（34）转化为矩阵形式为

进一步，取

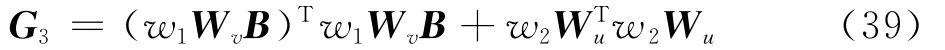
则式（37）可表示为

对式（40）两边同时乘以G3的逆矩阵，即可证明定理3。

由于复合式旋翼飞行器动力学模型复杂，且各操纵量受边界约束条件的限制，操纵量等式约束条件v（t）＝Bu（t）大多很难求解或存在u（t）不存在的情况，因此，该等式约束条件可转化为性能指标评价函数，可表示为

定理4 若复合式旋翼飞行器同时以指令跟踪误差最小和操纵量偏转量最小作为性能指标，并将操纵量等式约束条件转化为性能指标，则性能指标评价函数可表示为

操纵量Pareto最优解可近似表示为

证明 假设e′＝Bu－v，并忽略e′作为最优值的判断条件，则式（42）可近似表示为

若Γ′2取值最小，只需满足条件：

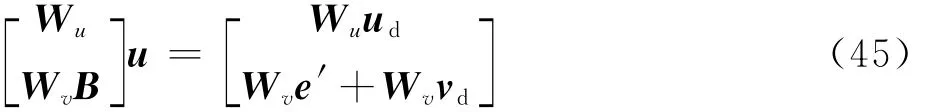
对式（45）左右两边同时乘以矩阵［WuwvB］，可得

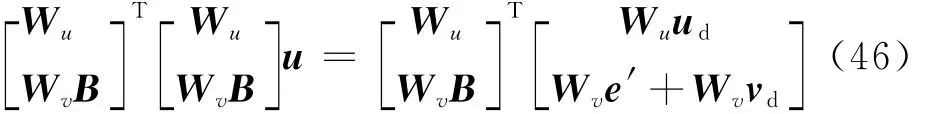
化简式（46）可得

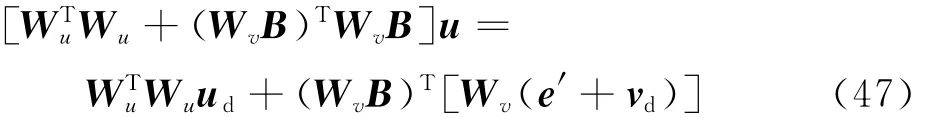
取G4＝WTuWu＋（WvB）TWvB ，并将e′替换为Bu－v，则可得

取G5＝G－14［（WvB）TWvB］，式（48）可表示为

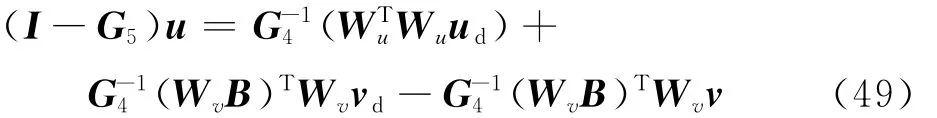
由于v与vd差值较小，且当f1取最小值时，可用vd近似表示v，故式（49）可近似表示为

则定理4得证。

由定理1～定理4可知，在操纵量权重系数和俯仰、偏航、滚转3通道权重系数确定的情况下，复合式旋翼飞行器混合多目标控制分配问题可通过数值计算求取性能指标评价函数Γ2＝f1＋f2＋f3的Pareto最优解求解。但仍需考虑复合式旋翼飞行器各操纵量权重系数和各通道权重系数对飞行器操纵效率的影响，将权重系数值作为性能指标评价函数的设计指标，通过动态变化权重系数值，提高操纵量控制效率。

已知操纵量权重系数矩阵Wu＝diag（wu1，wu2，…，wu8）为8阶对角矩阵，则各操纵量权重系数对所用操纵量权重系数均值的差值可表示为

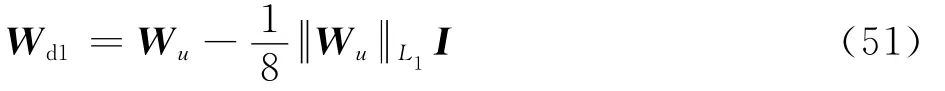
式中：WuL1为矩阵Wu的L1范数，表示矩阵Wu中所有元素之和，即8个权重系数之和。

为提高操纵效率，需保证各操纵量权重系数所对应的差值相同，即可转化为权重系数差值最大值最小化问题，可表示为

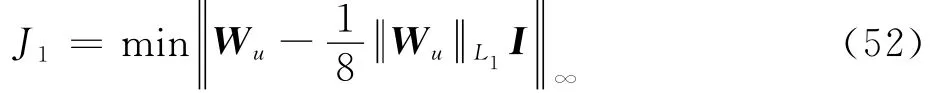
式中： ＊∞为矩阵的无穷范数，表示8个操纵量权重系数与均值的差值最大值。

同理，俯仰、偏航和滚转3通道所对应的权重系数矩阵Wv＝diag（wv1，wv2，wv3）为3阶对角阵，则3通道所对应的权重系数差值最大值最小化问题可表示为

式中：WvL1为矩阵Wv中3个通道的权重系数之和。

故权重系数性能指标评价函数可设计为

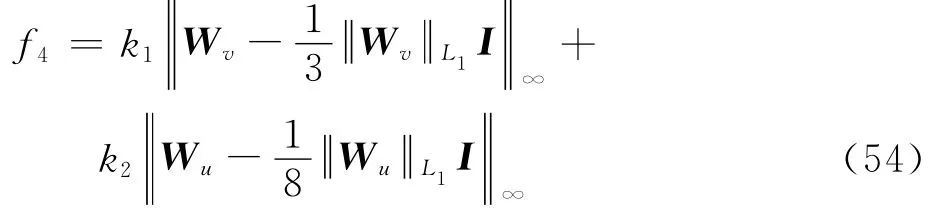
式中：k1、k2分别为俯仰、偏航和滚转3通道权重系数最大差值与操纵量权重系数最大差值所对应的比例系数。

综上，本文以指令跟踪误差最小、操纵量偏转量最小、控制分配操纵效率最高，及操纵量等式约束条件作为性能指标，同时考虑操纵量控制变量边界约束条件，则性能指标评价函数可表示为

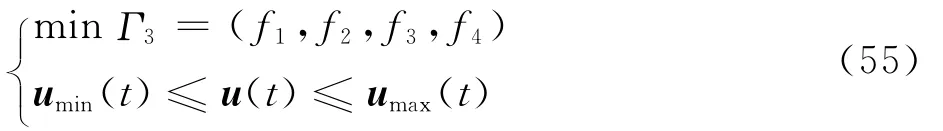
ud（t）和vd（t）为已知条件；Wu、Wv、u（t）和v（t）为未知量，考虑到该性能指标评价函数复杂，无法直接求解对应的Pareto最优解。首先，依据判断矩阵法设计各性能指标评价函数的权重系数wi，并利用线性加权和法，将混合优化问题转化为单目标优化函数，即

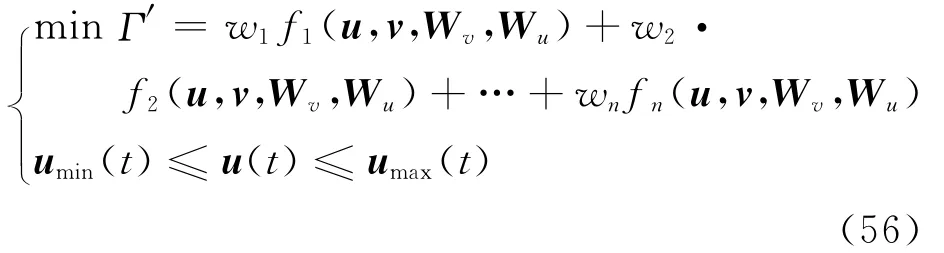
其中，判断矩阵法即通过判断对比两事件的相对重要程度，进而确定各事件的权重系数。

根据复合式旋翼飞行器飞行任务和飞行条件，分析n个性能指标函数的重要程度，并将n个性能指标进行排队，分别表示为事件S1，S2，…，Sn，然后依据专家经验分别进行两两判断，并对事件Si相对于Sj的重要程度进行分类并进行打分，具体如表2所示，并用2，4，…，10表示重要程度介于1，3，…，11。

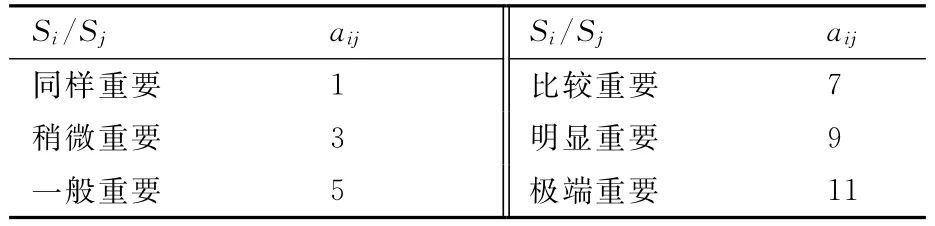
表2 判断矩阵重要程度指标Table 2 Index of judgment matrix importance

并计算可得判断矩阵为

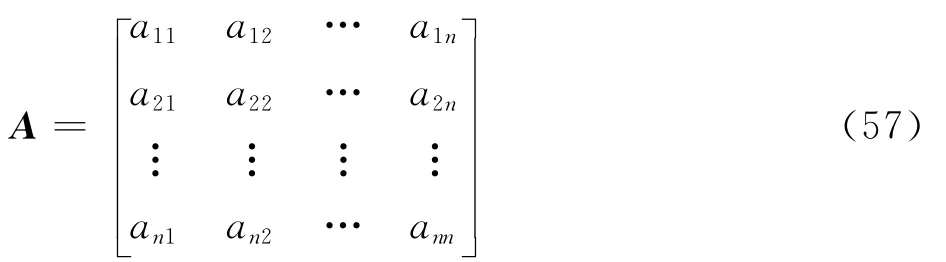
根据事件Si相对其他事件的重要程度ai1，ai2，…，ain，计算事件Si所对应的权重系数为

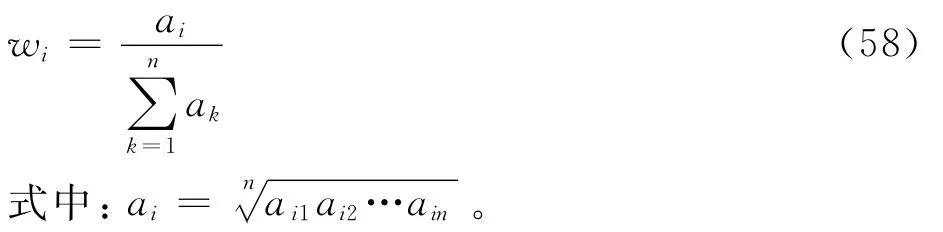
同时，为保证各事件间重要程度的协调性，对判断矩阵一致性进行判断。

通过随机一致性比率CR进行判断，即

式中：RI为平均随机一致性指标；CI为判断矩阵一致性指标，表达式为

式中：λmax为判断矩阵最大特征值。

当CR＜0.10时，则可认为判断矩阵A满足一致性，否则需重新调整判断矩阵。

由此，混合多目标优化控制分配策略优化目标函数可表示为

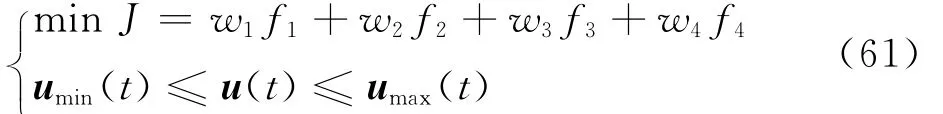
随后，针对这一混合优化目标，本文采用改进的粒子群算法，动态改变操纵量权重系数矩阵Wu，控制通道权重系数矩阵Wv，实时操纵量在线寻优，实现复合式旋翼飞行器模式切换过渡过程操纵量控制分配，保证飞行器快速准确跟踪控制指令，同时，提高控制面操纵效率，减少舵面耗能。该控制策略具体实施方法如图3所示。

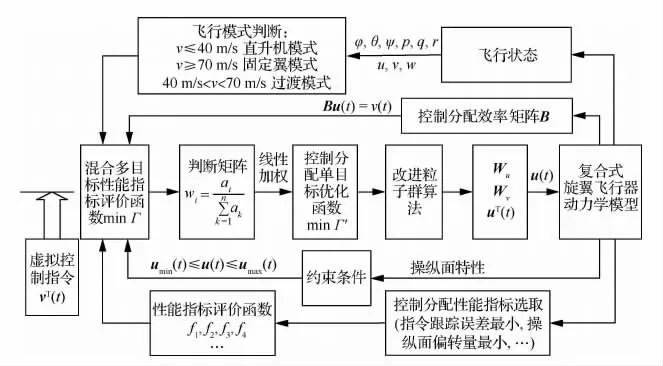
图3 多目标优化控制分配策略Fig.3 Allocation of multi-objective optimization control

2.3 改进粒子群优化算法设计

复合式旋翼飞行器动力学模型复杂，若采用传统的寻优算法对复合式旋翼飞行器控制分配优化目标函数进行求解，可能陷入局部最优解或寻优耗费时间长，导致复合式旋翼飞行器控制系统的稳定性较差，且可能产生不稳定的情况，因此，本文提出一种改进的粒子群算法，提高寻优速度和精度，同时可保证控制性能指标最优。实现粒子群算法的基本过程如下：

步骤1 确定粒子群的适应度函数min J＝w1f1＋w2f2＋w3f3＋w4f4，粒子群优化个体x＝［uTw′vw′u］，w′v＝ ［wv1wv2wv3］为 俯仰、滚转和偏航3通道权重系数，w′u＝［wu1wu2wu3wu4wu5wu6wu7wu8］为8个操纵量所对应的权重系数。

步骤2 对粒子群算法进行初始化，具体包括粒子群粒子数量N，惯性权重系数ww，最大迭代次数Tmax，学习因子c1、c2，终值误差τ，粒子群更新最大速度为vmax和初始化粒子xi，粒子种群位置xd（t）＝ ［x1dx2d… xid… xNd］，速度v（t）＝ ［v1v2… vi… vN］，其中t表示迭代次数。

步骤3 将初始化粒子群代入粒子群适应度函数，求解性能指标，得到粒子第t次迭代的个体最优值pib（t）和全局最优值pb（t）。

步骤4 更新粒子群的速度vi（t＋1）和位置xid（t＋1）。

由于粒子群算法的求解速度和精度与粒子群速度进化公式中的惯性权重ww密切相关，ww的大小决定了粒子群算法粒子群算法全局搜索能力和局部搜索能力，因此，合理的ww能够加快粒子群算法寻优速度，提高粒子群算法最优解精度。

本文综合每个粒子的当前适应值，全局最优值，全局最差值，利用反正切函数改变ww，使ww随粒子当前的位置和速度而改变，使粒子群求解过程中前期ww值较大，提高全局搜索能力，加快求解速度，后期ww较小，提高局部搜索能力，保证求解精度，具体表达式为

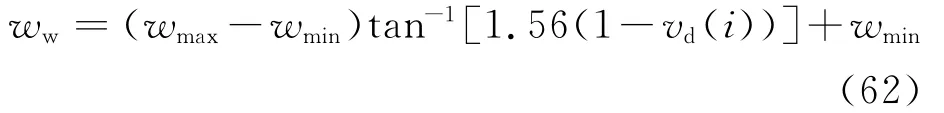
式中：wmax为最大惯性权重系数；wmin为最小的惯性权重系数；vd（i）为第i个粒子的收敛速度，vd（i）数值越小，表示第i个粒子距全局最优值的位置越靠近，vd（i）的具体表达式为

式中：pi（T）为迭代次数T下的适应值；pb（T）为迭代次数T的全局最优值；pw（T）为迭代次数T的全局最差值。

粒子群算法的速度和位置更新公式为

式中：r1、r2为区间在 ［0，1］之间的随机数。

步骤5 将新的粒子种群xid（t＋1）代入粒子群适应度函数，求解性能指标，更新个体最优值pib（t＋1）和全局最优值pb（t＋1）。

步骤6 重复步骤4～步骤6，直到全局最优值满足终值误差条件或达到最大迭代次数，并将全局最优值中的操纵量uT（t）作为复合式旋翼飞行器的实际操纵量Pareto最优值。

改进的粒子群算法实现流程图如图4所示。

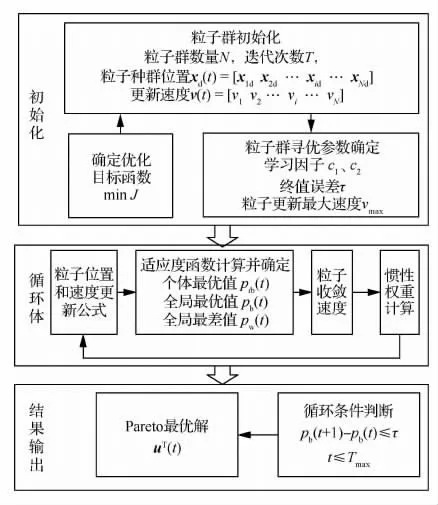
图4 改进的粒子群算法实现过程Fig.4 Procedure of improved particle swarm optimization algorithm

3 仿真验证

选取已建立的近似X-49复合式旋翼飞行器的动力学模型为研究对象，在基于赋权多目标混合优化的控制分配策略下，分别完成复合式旋翼飞行器从直升机模式下40m／s到固定翼模式下70m／s和从固定翼模式下70m／s到直升机模式下40m／s的过渡模式飞行仿真，验证该控制分配策略的可行性。

复合式旋翼飞行器过渡飞行模式下，操纵量u（t）的取值范围为

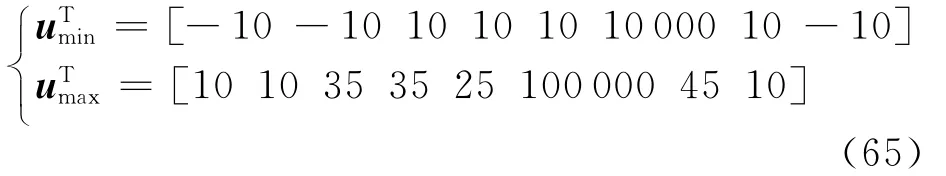
根据飞行任务，选取f1、f2、f3和f4作为性能指标评价函数，假设性能指标评价函数重要程度依此排序为：f4、f1、f3和f2，根据判断矩阵法，可求得性能指标评价函数所对应的判断矩阵为

由判断矩阵可求得最大特征值λmax＝4.0511，CI＝0.017，RI＝0.89。

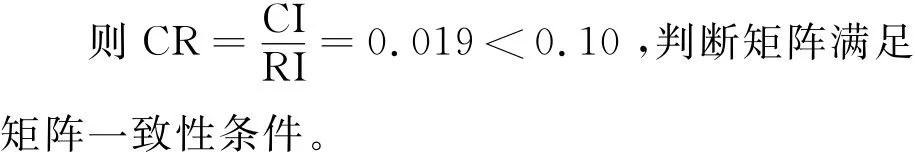
并根据判断矩阵可求得权重系数为

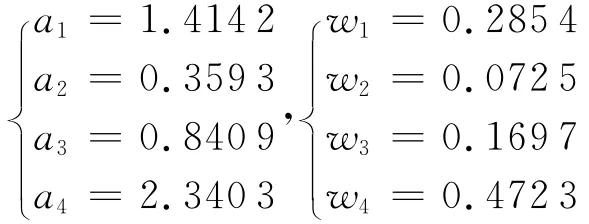
故该控制分配策略的优化目标函数为

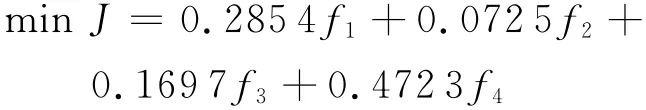
设定粒子群粒子数量N＝50，参数wmin＝0.4，wmax＝0.9，最大迭代次数Tmax＝1 000，学习因子c1＝c2＝2，粒子更新最大速度为vmax＝5，在线更新俯仰、偏航和滚转3通道权重系数wv1、wv2、wv3和操纵量权重系数wu1，wu2，…，wu8，动态改变复合式旋翼飞行器操纵量，完成速度指令跟踪仿真，仿真结果如图5～图9所示。其中，40～70m／s速度指令跟踪仿真耗时68.126 491s，每一步迭代所耗时间大约为3.406 3ms；40～70m／s速度指令跟踪仿真耗时76.834 601s，每一步迭代所耗时间大约为2.561 2ms；实际工程应用采样时间大约为10ms，故该控制策略应用于实际工程，能够实现控制信号的实时分配。

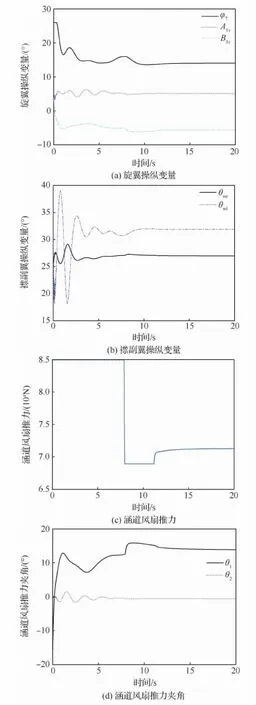
图5 过渡模式下40～70m／s操纵量变化曲线Fig.5 Variation curves of 40-70m／s manipulated variable in compound rotorcraft transition mode

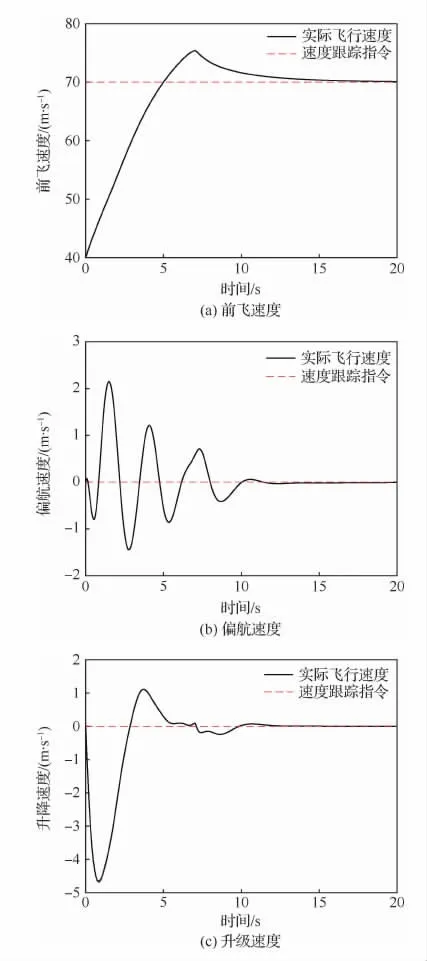
图6 过渡模式下40～70m／s速度变化曲线Fig.6 Variation curves of 40-70m／s speed in compound rotorcraft transition mode

由图5和图8可知，虚拟控制指令v（t）经控制分配后可得到复合式旋翼飞行器8个操纵量，并直接作用于复合式旋翼飞行器，有效解决了操纵冗余问题。当复合式旋翼飞行器完成速度指令跟踪后，各个操纵量均稳定于一常值，由此可知，当复合式旋翼飞行器完成速度指令跟踪后作定常直线飞行时，各操纵量几乎保持不变，复合式旋翼飞行器操纵简单，降低了驾驶员的工作负担。

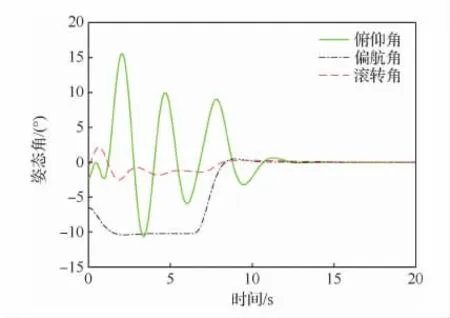
图7 过渡模式下40～70m／s姿态角变化曲线Fig.7 Variation of 40-70m／s attitude angle in compound rotorcraft transition mode

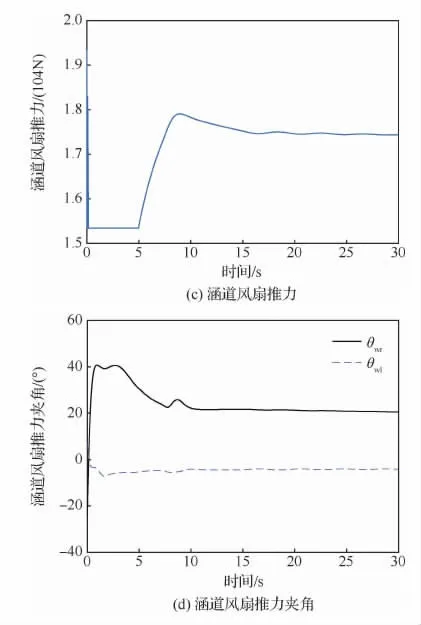
图8 过渡模式下40～70m／s操纵量变化曲线Fig.8 Variation curves of 40-70m／s manipulated variable in compound rotorcraft transition mode

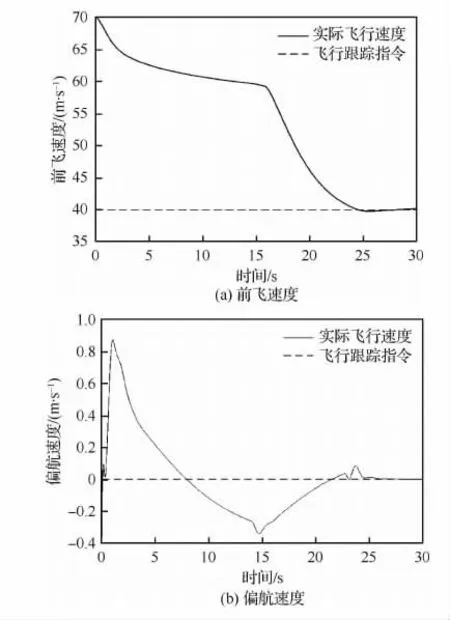
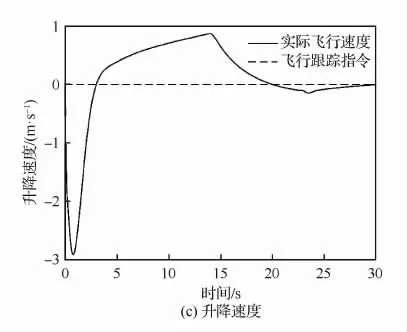
图9 过渡模式下40～70m／s速度变化曲线Fig.9 Variation curves of 40-70m／s speed in compound rotorcraft transition mode

图6 和图9表示复合式旋翼飞行器过渡模式下速度变化曲线，由图6可知，复合式旋翼飞行器在15s内可完成速度指令跟踪，且完成指令跟踪后，前飞速度保持70m／s匀速飞行，偏航速度和升降速度保持不变，复合式旋翼飞行器稳定飞行；图9中复合式旋翼飞行器完成速度指令跟踪耗时较长，且前飞速度和偏航速度波动较大，但最终可以实现模式切换平稳飞行。图7表示复合式旋翼飞行器过渡模式下姿态角变化曲线，图7表明，复合式旋翼飞行器完成速度指令跟踪后，飞行器3个姿态角稳定。

同时，为验证改进的粒子群算法能够改善复合式旋翼飞行器飞行控制系统的稳定性，图10和图11给出了复合式旋翼飞行器分别采用经典粒子群算法及改进粒子群算法的优化算法下，模式切换过渡过程姿态角和速度随时间的变化曲线。其中，在经典粒子群优化算法下，40～70m／s速度指令跟踪仿真耗时83.735 463s，每一步迭代所耗时间大约为4.186 8ms，所耗时间明显大于改进的粒子群算法，故改进的粒子群算法的实时性更好。

图10表示复合式旋翼飞行器3个姿态角随时间的变化曲线，由图10（c）可见，基于经典粒子群算法的赋权系数混合多目标优化控制分配策略完成指令跟踪后，滚转角稳定性较差；由图11（a）可知，基于改进粒子群算法的赋权系数混合多目标优化控制分配策略完成速度指令的跟踪时间较短。故由图10和图11可知，本文提出的基于改进粒子群算法的复合式旋翼飞行器混合多目标优化控制分配策略可使得复合式旋翼飞行器过渡切换更平稳、耗时更短，保证系统的稳定性。

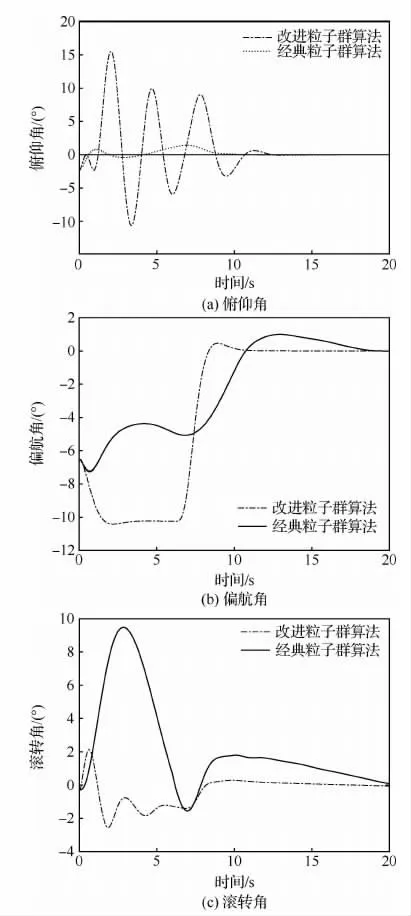
图10 复合式旋翼飞行器过渡模式下姿态角变化曲线Fig.10 Variation curves of attitude angles of compound rotorcraft in transition mode

4 结 论

1）本文研究复合式旋翼飞行器直升机模式与固定翼模式相互切换时过渡过程的舵面操纵特性，提出基于赋权多目标混合优化的控制分配策略，仿真验证该控制分配策略可有效解决复合式旋翼飞行器带约束受限的舵面操纵冗余问题，使得系统快速跟踪控制指令。

2）本文提出了一种改进的粒子群算法，可动态更新操纵量及控制通道权系数矩阵，快速求解复合式旋翼飞行器操纵控制变量，提高控制面操纵效率，改善飞行器控制系统的鲁棒性，仿真结果验证该方法的可行性，相比于经典粒子群算法寻优，具有更好的控制效果。