基于复合地标导航的动平台四旋翼飞行器自主优化降落技术

邢伯阳，潘峰，2，王位，冯肖雪，＊

1.北京理工大学 自动化学院，北京 1000812.北京理工大学 昆明产业技术研究院，昆明 650106

四旋翼飞行器自主着陆技术对其在自动充电和物流配送等领域的应用都有着非常重要的研究意义。目前已有许多研究成果实现了在静止目标上的降落，文献［1］基于全球定位系统（GPS）和惯导传感器（IMU）作为机载导航设备，结合着陆点的激光反射装置，使用降落目标的经纬度作为返航降落点实现了高精度的自动降落，另外还有采用视觉里程计［2］等机器视觉技术替代GPS的方案。基于可靠性、成本和计算量的综合考虑，采用二维地标引导的自主降落系统备受关注，其核心是使用二维地标提供飞行器机载相机相对自身的实时位姿，从而辅助飞行器自主降落。如文献［3］采用了一种双圆环图案的地标为无人机自主降落提供可靠的视觉定位数据。文献［4］在圆环地标内增加字符不对称设计，实现了基于单一圆环对相机六自由度（6DoF）位姿的估计。另外还有一些研究成果采用二维码实现了在静止目标上的可靠降落［5］。

相比于静止目标，在车辆或船舶等动平台上的自主降落更具实用价值。其最大的难点在于降落目标的位置会不断改变，因此对动平台精确位姿的测量和如何规划出高效降落轨迹是其中的难点，目前相关文献主要通过3方面策略来实现在动平台上的地标引导降落。

1）二维地标定位技术

二维地标定位已被广泛应用于静目标降落系统中，许多学者进一步对现有二维地标做出改进以获得更可靠的识别和更连续的定位数据。文献［6］使用红蓝色块地标，实现了在动平台低慢速和直线运动下的飞行器自主降落，但由于地标尺寸固定使得其存在较大死区，因此在低空降落中往往因为地标不完整识别而导致降落失败。为减小地标定位死区，研究人员提出采用多尺寸地标组合或动态调整地标大小的方式，文献［7］在二维码内部编码空白处增加小尺寸二维码有效减小了定位死区，文献［8］采用多个不同尺寸二维码并排布置实现了在不同距离上高精度的相机定位。文献［9］则直接采用一个显示屏依据其离飞行器的距离来动态改变地标的尺寸。

2）动平台状态估计技术

由于二维地标需要完整识别才能提供定位数据，因此在实际应用中其数据往往不连续并且存在噪声。有学者提出通过建立动平台运动模型结合异构传感器信息来估计其精确连续的位姿。文献［10］建立了动平台的线性运动模型，将GPS数据与码盘数据融合实现了对动平台连续位姿的在线估计。类似的系统在文献［11］中也被提出，但作者使用二维码来代替GPS并基于平台直线运动假设设计运动模型。为解决动平台运动中的非线性问题，一些学者使用扩展卡尔曼滤波器（EKF）［12］设计状态估计器得到了更精确的位姿估计结果。

3）降落轨迹规划技术

在得到动平台精确位姿估计后，最直接的方式是采用位置闭环控制飞行器降落。文献［13］采用线性二次型控制器进行位置闭环控制实现了飞行器初步的动平台降落，该系统简单易于实现但未考虑动平台存在突发机动的情况导致降落成功率较低。因此一些研究学者提出采用最优控制理论来设计高效降落轨迹的方案，降落轨迹除了需要准确通过预设航点外还需要尽可能地减少降落能量消耗，文献［14］采用最小Snap指标来设计降落轨迹，并基于最小值原理求解出其最优解。文献［15］则将降落轨迹规划考虑为二次型最优化问题并设计算法实现了在复杂环境下的轨迹规划，但由于其采用不等式约束使得计算量较大难以在低成本嵌入式平台上保证实时性。

综上，动平台精确降落对视觉定位的准确性、状态估计的鲁棒性以及降落策略的高效性都有较高要求。现有系统存在地标定位死区大，状态估计不精确、鲁棒性差以及降落策略简单和轨迹规划算法计算量大等问题。为解决以上问题本文设计了一个基于复合地标导航的动平台优化降落系统。所提系统采用圆环和二维码构成复合地标来实现对机载相机的实时定位。通过建立精确的运动模型并利用扩展卡尔曼滤波理论实现对动平台在车轮打滑或码盘标定不精确等情况下的精确位姿估计。最终以最小轨迹Jerk指标设计降落轨迹保证快速高效的降落。通过仿真和实际降落实验验证了所提系统具有估计动平台连续实时位姿估计的能力，基于该系统实现了飞行器在动平台处于直线或圆形轨迹运动下的平稳可靠降落。

1 基于复合地标的相机定位算法

1.1 复合地标设计与识别算法

为实现对动平台离飞行器在不同距离上的连续精确定位，本文设计了如图1所示的C2D地标并将其布置于动平台顶部。C2D地标由圆环子地标（T-C）和二维码子地标（T-D）组成，其中 T-C地标带有缺口设计，其外圆直径为do，内圆直径为di；T-D地标布置于T-C地标圆心处其尺寸为d2D。C2D地标识别流程如图2所示。

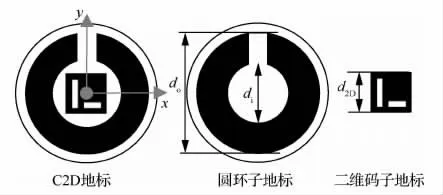
图1 C2D地标Fig.1 C2Dlandmark

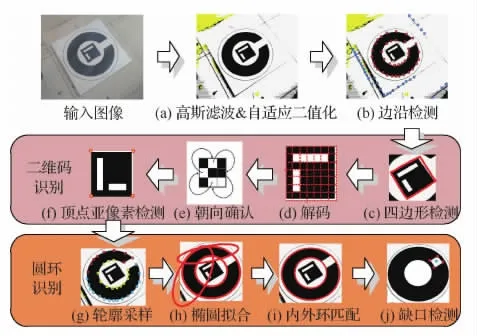
图2 C2D地标识别流程Fig.2 Detection flow chart of C2Dlandmark

算法首先对原始图像进行如图2（a）所示的6×6模板高斯滤波和自适应二值化处理［16］，然后对图像中T-D地标进行识别。采用Canny算子提取轮廓（图2（b）所示）并在轮廓集合中筛选凸四边形拟合结果。图2（c）～图2（d）对四边形内部编码信息进行校验并确定T-D地标编号和正确朝向，最后对识别到T-D地标的顶点进行亚像素检测得到4个顶点精确的2D-3D匹配关系（图2（f）所示）；对T-C地标来说，首先对剩余轮廓进行如图2（g）所示的分段采样，进一步对采样点集合进行椭圆拟合得到如图2（h）所示的椭圆集合。依据T-C地标设计参数、椭圆中心误差、长轴角度误差和长短轴比例误差加权得到综合匹配误差，最终选择集合中2个综合匹配误差最小的椭圆作为内外环识别结果（如图2（i）所示）。另外，当已识别到T-D地标时可直接使用其中心点像素位置来快速筛选椭圆集合。为方便识别缺口位置，本文使用内外环椭圆与圆环轮廓构成如图2（j）所示的缺口二值化图，并通过检测其中凸四边形轮廓来确定缺口位置。

1.2 基于C2D地标的相机位姿估计

C2D地标由T-D地标和T-C地标构成，其中T-D地标提供近距离时的相机定位，T-C地标提供远距离时的相机定位，二者使用的相机位姿估计算法如下所述。

1）基于T-D地标的相机6DoF位姿估计

基于所提识别算法可以得到T-D地标4个顶点的2D-3D匹配关系，本文使用高效N点透视定位（EPNP）算法［17］来快速地计算出相机在 T-D地标坐标系下的旋转矩阵Rd和平移向量Td。

2）基本点基于T-C地标的相机6DoF位姿估计

在完成对T-C地标的识别后可以通过其外环椭圆投影估计出其在相机坐标系下5DoF位姿，进一步结合缺口来对地标进行朝向估计从而得到其完整的6DoF位姿。为不失一般性，首先给出由任意椭圆投影估计地标5DoF位姿的算法。

首先，使用相机内参将椭圆投影转换到归一化相机坐标系下并由识别结果计算出椭圆圆心和长短轴参数Li（i＝1，2，…，6），则可构建椭圆参数方程：

进一步可以得到椭圆圆锥投影矩阵Q为［4］

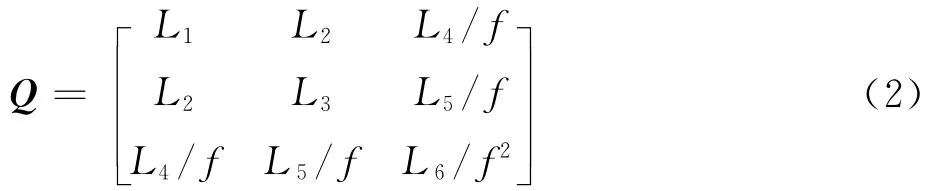
式中：f为摄像头焦距。

设λ1、λ2和λ3为Q 矩阵的特征值，ε2、ε3为λ2、λ3的特征向量。假设λ1＞λ2＞0＞λ3，则圆环平面在相机坐标系下的角度和位置为

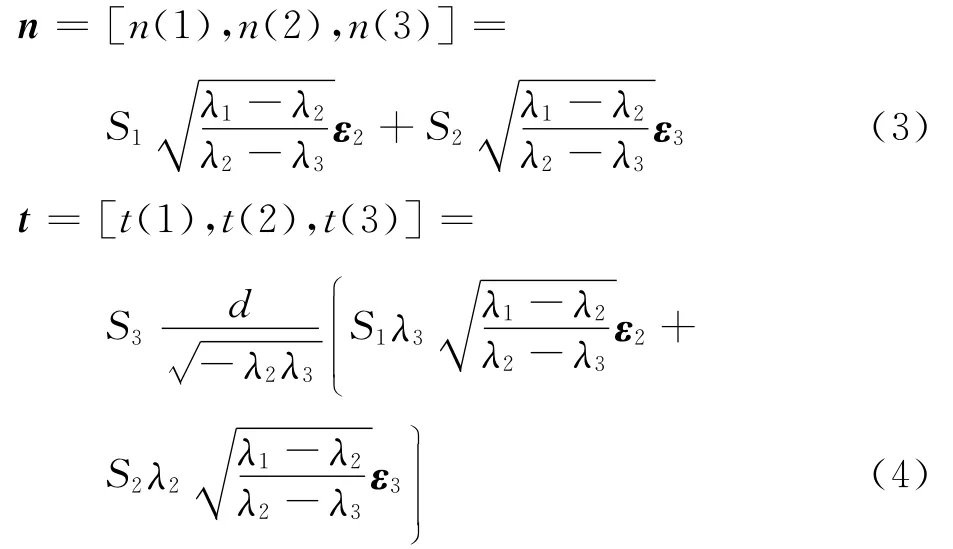
式中：d为圆环直径。

式（3）和式（4）中S1、S2和S3未定正负号，同时单一椭圆投影无法得到地标朝向，因此基于式（3）和式（4）只能得到相机5DoF旋转矩阵rc和平移向量tc的奇异解：

基于地标在相机前方且地标z轴朝向相机光心能构造n［0，0，1］T＜0和t［0，0，1］T＞0两个约束条件，并筛选出两组奇异解。随后本文基于T-D地标定位数据和机载IMU数据进行二次筛选。

1）由于T-D地标坐标系和T-C地标坐标系重合，因此T-D地标在相机坐标系下的位姿应当与T-C地标一致，则当识别到T-D地标时可直接选择奇异解中与其位姿结果相近的作为正解。

2）在T-D地标无法识别时，本文采用IMU解算姿态角作为筛选条件，假设动平台处于水平地面并忽略平台倾斜引起的误差，由于相机与IMU相对安装关系RIc已知，则可采用RIMU＝RIcRI作为判断条件对奇异解进行筛选，RI为相机在全局坐标下的旋转矩阵。为简化奇异解筛选过程，本文直接采用欧拉角作为比较对象，则已知旋转矩阵R＊和平移向量t＊由它们计算出的相机在欧拉坐标系下的位姿为ζ＊为

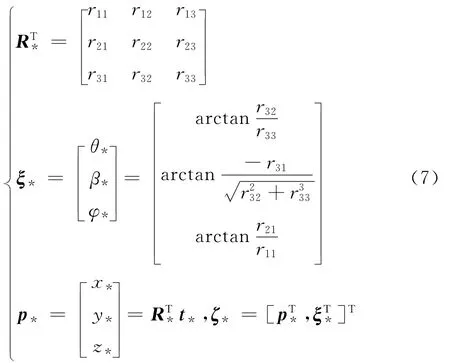
定义基于式（7）最终筛选出的T-C地标坐标系下的相机5DoF位姿正解为r＊c、t＊c，进一步为得到其完整的6DoF位姿，本文使用缺口中心像素和T-C地标中心像素来近似计算朝向：

式中：［Scx，Scy］T为 T-C 地标中心像素坐标，［Hx，Hy］T为缺口中心点像素坐标，则 T-C地标坐标系下相机完整6DoF位姿为

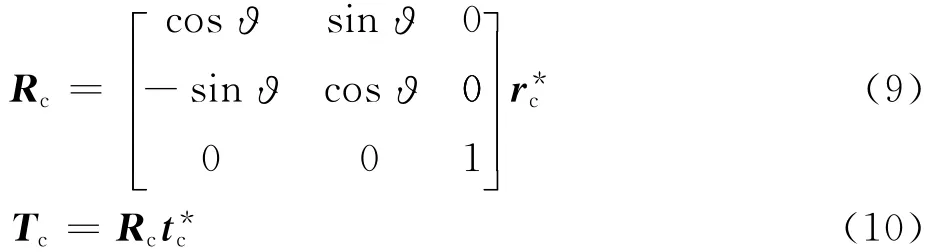
3）基于C2D地标的相机位姿估计

由式（1）～式（10）可以得到 T-D地标和 T-C地标坐标系下的相机位姿估计。若某一子地标被单独识别则C2D地标定位结果等于该子地标的定位结果。若两个子地标同时被识别时，本文采用T-D地标4个顶点的平均二次投影误差构建融合权重来对二者定位结果进行线性加权融合（近距离时T-D地标角点检测精度高则权重大，远距离时T-D地标角点检测精度下降则权重小）。定义由T-D地标得到的相机位姿为ζ2D，由T-C地标得到的相机位姿为ζc，则最终由C2D地标提供的相机位姿ζC2D＝［xC2D，yC2D，φC2D］T为

式中：e2D为T-D地标4个顶点二次投影误差平均值；emax为设定的最大投影误差。

2 动平台位姿估计算法

为了得到动平台精确连续的位姿和速度估计，本文基于扩展卡尔曼滤波器（EKF）来设计动平台状态估计器。下文采用三轮全向底盘作为动平台来介绍状态估计算法，其坐标系描述如图3所示。

图3中动平台机体半径为L，顶部布置有C2D地标。从图3中可以看到动平台机体坐标系与C2D坐标系对齐，定义机体坐标系为｛m｝，其原点在机体中心，ym轴指向机头和缺口方向，xm和zm轴满足右手法则；定义动平台在全局坐标系｛n｝下的位置为 ［x，y，φ］T，机头朝向为φ，则可得到三轮全向底盘运动模型为

图3中的三轮全向平台正运动学驱动模型［18］为

图3 动平台坐标系示意图Fig.3 Coordination of moving platform

式中：wi（i＝1，2，3）为各轮线速度；vmx和vmy为动平台机体线速度；ω为机体角速度；F为驱动变换矩阵。

2.1 状态预测

在理想情况下，基于式（13）和式（14）仅利用码盘数据就能实现对动平台位姿的估计，但是由于码盘数据存在噪声和误差，最终造成位姿估计结果会存在累计误差。同时在实际应用中动平台往往在复杂地面上移动，其存在着车轮打滑等未知因素，如动平台某轮悬空于地面缝隙或者动平台被障碍物阻塞等情况都会造成码盘数据与真实数据的不符，如直接使用包含测量偏差数据进行状态预测势必会产生严重的误差并最终导致降落失败，因此为解决该问题本文进一步对码盘偏差进行建模。

定义动平台系统状态为X＝ ［x，y，φ，vmx，vmy，ω，e1，e2，e3］T，其包括动平台在｛n｝系下的位置和朝向，｛m｝系下的速度和角速度以及各码盘测量偏差。另外，基于以下两点考虑，本文将机体速度vmx、vmy包含在系统状态中：

1）方便引入其他传感器来测量vmx、vmy、ω，如采用陀螺仪来测量动平台角速度，采用光流传感器来测量动平台更精确的线速度。

2）由于码盘数据需要通讯传输，而通讯造成的延时更容易在量测更新中通过时间戳或环形队列进行补偿。

综上，结合动平台非线性模型和系统状态构建滤波器状态转移方程为

式中：ηk为系统过程噪声，本文假设其为高斯白噪声（协方差矩阵为Qk），则k＋1时刻Xk＋1的预测值为

式中：T为采样周期。基于EKF滤波算法k＋1时刻系统状态Xk＋1的预测协方差矩阵P－k＋1为

式中：fx为f（·）的雅克比矩阵。

2.2 状态量测更新

量测更新使用C2D地标定位结果和码盘速度测量值来对预测状态进行修正，则量测向量zk＋1和量测方程h（·）间的关系为

式中：σk＋1为量测噪声。C2D地标仅能提供｛m｝系 下 的 相 机 位 姿 ζC2D（k）＝ ［xC2D（k），yC2D（k），φC2D（k）］T，因此需要使用四旋翼飞行器全局状态估计ζq（k）＝ ［xq（k），yq（k），φq（k）］T进行坐标变换，则 C2D 地标提供的量测向量zc（k＋1）＝ ［xm（k＋1），ym（k＋1），φm（k＋1）］T 为

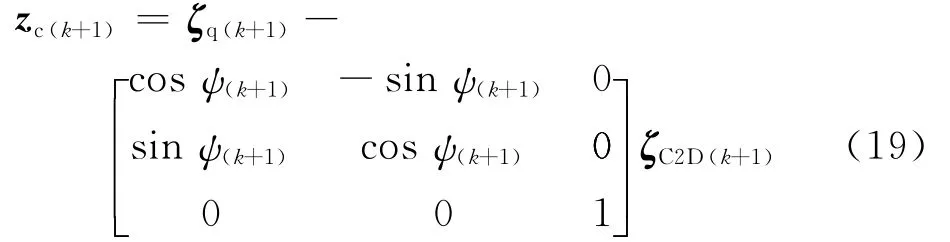
式中：ψ（k＋1）＝φq（k＋1）－φC2D（k＋1）为 C2D 地标在｛n｝系下的朝向，另外量测数据中还包括了码盘测量到的各轮线速度，对于码盘数据滞后本文采用文献［19］所提出的环形队列和时间戳技术进行补偿，则 码 盘 提 供 的 量 测 向 量 为 ze（k＋1）＝［w1（k＋1），w2（k＋1），w3（k＋1）］T，最终定义滤波器量测向量为zk＋1＝ ［zTc（k＋1），zTe（k＋1）］T，根据 EKF滤波算法其预测值为

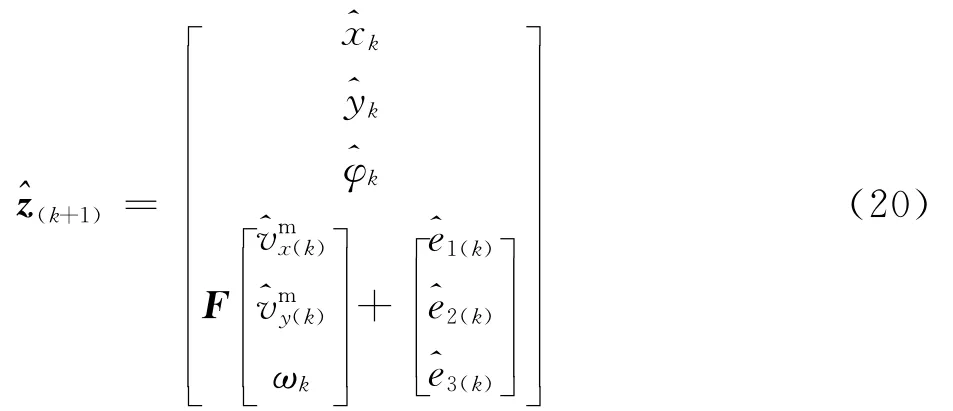
定义残差向量νk＋1为量测向量和其预测值之差，则残差向量和其近似协方差矩阵为

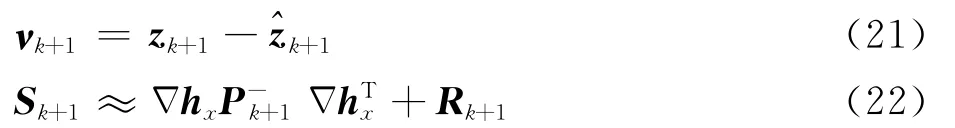
式中：hx为h（·）的雅克比矩阵；Rk＋1为量测噪声σk＋1的协方差矩阵。则卡尔曼增益为

最终，动平台修正后的状态估计和协方差矩阵为

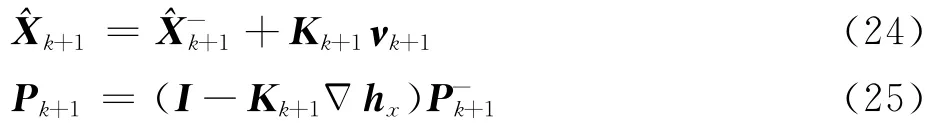
式中：I为单位矩阵。综上，基于式（15）～式（25）可以实现对动平台连续状态的在线估计，并为后续降落规划提供可靠的反馈数据。

3 动平台降落规划算法

为实现高效可靠的动平台降落，本文以最小化轨迹Jerk指标来设计降落轨迹，所提算法同时考虑降落过程中动平台机动和降落能量消耗问题，降落轨迹示意图如图4所示，图中黑色轨迹为动平台运动轨迹，红色轨迹为四旋翼飞行器降落轨迹，蓝色箭头为动平台当前速度矢量Vc。降落开始后，飞行器首先采用图像跟踪的方式从远处快速逼近动平台，在达到切换边界点P1（t）后基于动平台和飞行器实时位姿估计规划降落轨迹。降落轨迹除了需要保证飞行器在动平台后方P2（t）航点处稳定跟随外还需要以最小能量消耗为指标降落在P3（t）航点处，所提优化降落策略如下所述。

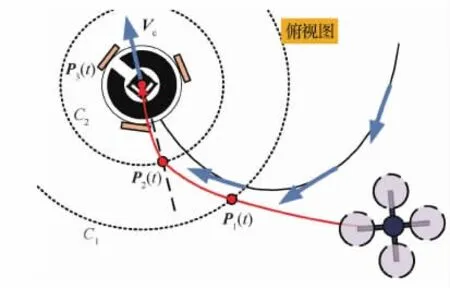
图4 降落轨迹示意图Fig.4 Landing trajectory

1）跟踪边界点P1（t）

在识别到动平台后，飞行器基于图像跟踪的方式向动平台直线逼近。其以C2D地标中心像素位置与图像中心作反馈控制，x轴误差控制四旋翼飞行器航向，y轴误差控制云台俯仰角。逼近中飞行器保持高度H1，前进速度V1。定义R1为最小逼近距离，D（t）为飞行器离动平台的实时直线距离：

式中：＾zq（t）为飞行器当前估计高度；θp（t）为云台俯仰角度；ρ（0＜ρ＜1）为可调权重参数，则当D（t）小于R1时进行模式切换。

2）降落切换点P2（t）

该模式下飞行器需要规划降落轨迹实现在动平台后方的稳定跟随，因此本文选择动平台当前速度矢量Vc（t）反方向延长线与圆环C2交点作为P2（t）＝ ［x2（t），y2（t），z2（t）］T航点，则其坐标为

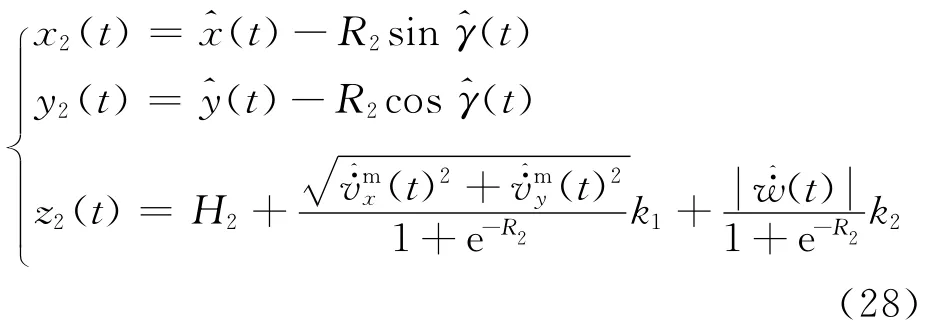
3）降落目标点P3（t）

在经过P2（t）航点后飞行器进入最终降落阶段，本文基于最小能量消耗来动态选择P3（t）降落点，首先以时间间隔dT来预测动平台未来n·dT（n＝1，2，…，m）时刻的位置作为候选降落点。通过对候选轨迹的Jerk进行积分作为其能量消耗［20］，并选择能量消耗最少的作为降落航点P3（t）＝ ［x3（t），y3（t），z3（t）］T。

综上，所提降落轨迹不但要满足航点约束外还需具有最小能量消耗，该问题为一个典型的二次最优规划问题。为简化计算本文对三维轨迹独立进行规划，考虑某一维轨迹可由n阶多项式表示，其多项式参数向量为p ＝ ［p0，p1，…，pn］T，采用最小化轨迹Jerk指标设计降落轨迹的数学描述为

式中：k为轨迹分段数量；ti（i＝1，2，…，k）为各段轨迹始末时间。

进一步由航点信息构建如式（30）所示的约束，轨迹起始点为飞行器当前位置，轨迹中点需通过P2（t）航点，轨迹末端终止在P3（t）航点，另外在P2（t）航点前后两段轨迹的位置、速度和加速度应当连续，则以x轴轨迹规划为例其等式约束如下：

进一步结合本文第1节所提地标定位算法和第2节所提动平台状态估计算法给出如图5所示的降落系统设计。其采用层次化和模块化设计理念，包括：① 传感器层由多种异构传感器组成包括所提C2D地标、码盘、惯导传感器和二维码阵列定位系统；② 数据融合层采用异构传感器数据和所提状态估计算法对飞行器和动平台的位姿进行在线估计；③ 决策层结合动平台与飞行器的实时状态估计执行所提降落策略，并规划降落轨迹；④ 控制层实现飞行器对降落轨迹的跟踪控制，同时使用C2D地标像素识别结果完成云台对目标的跟踪对准控制。

图5 降落系统框架图Fig.5 Flow chart of landing system

4 实验与分析

为验证本文所提优化降落系统，本文搭建了一个四旋翼飞行器和三轮全向移动平台。飞行器轴距为330mm，使用8045螺旋桨和980kV的无刷电机，整机重量为1.2kg，续航时间为15min。由式（19）可知动平台在｛n｝系下的量测向量需使用飞行器全局位姿进行坐标系变换，为获得飞行器精确的位姿数据，实验使用文献［21］中提出的二维码阵列定位系统实现飞行器导航和定位。为降低图像抖动并实现可靠图像跟踪，飞行器前方安装有两轴云台和PS2Eye相机（可提供320×240，60FPS的图像数据）。所提地标定位算法，动平台状态估计算法和降落轨迹规划算法均在机载Odroid-Xu4处理器中运行。三轮全向底盘高度为20cm，半径L为35cm，C2D地标外环直径do为55cm，di为40cm，二维码尺寸d2D为34cm。飞行器通过2.4G射频基站与动平台通讯，频率为50Hz，丢包率小于5%。

4.1 C2D地标定位实验

本文首先对C2D地标定位性能进行验证。图6（a）中给出了相机在｛m｝系下的各地标提供的3D定位结果，图中曲线恒为零时表示该地标无法识别，可见T-C地标和T-D地标都仅能实现相机在｛m｝系下部分区域的定位，而所提C2D地标定位算法则实现了相机在｛m｝系中较完整的3D定位。图6（b）给出了C2D地标距离相机不同直线距离上的定位误差曲线（图中定位误差为1时表示该地标无法识别），其中三角形标记线为T-D地标定位误差曲线，可以看到其提供了0.5～3.5m间的相机定位数据，其定位误差随距离增大而增加；红色矩形标记线为T-C地标定位误差曲线，可以看到其提供了1.5～6.0m的相机定位数据，并且其定位精度在不同距离上变化不大；黑色十字标记线为C2D地标定位曲线，可看到其通过综合T-C地标和T-D地标结果实现了距离在0.5～6.0m内的相机综合完整定位。复合地标既适用于近距离定位也适用于远距离定位，定位精度最高可达到0.1m。

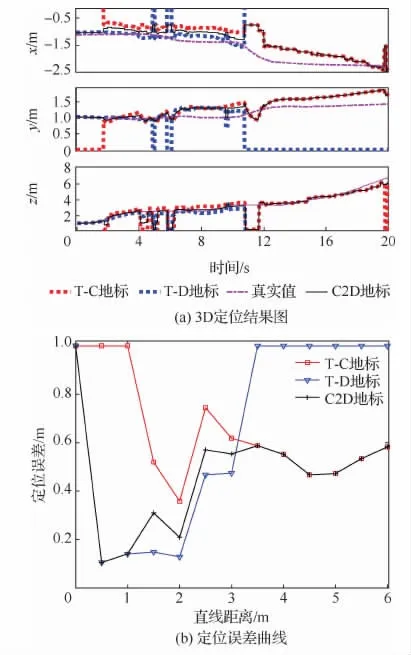
图6 C2D地标定位结果图Fig.6 Localization results of C2Dlandmark

4.2 状态估计仿真实验

为验证所提动平台位姿估计算法，本文设计如下仿真实验。实验中飞行器悬停在坐标点（0，0，3）m处，动平台以（1，3，0）m为圆心进行半径为2.0m的圆形轨迹运动，速度矢量模值为1.0m／s。为对比算法性能，实验与文献［11］中所提出未考虑测量偏差的EKF算法进行对比。实验中为码盘1添加缓增测量偏差；在7s时为码盘2突加0.2m／s固定测量偏差，码盘3添加－0.4m／s固定测量偏差；在17s后为码盘2和码盘3添加幅值为0.4m／s的正弦偏差，实验结果如图7和图8所示。

图7 动平台位置估计结果Fig.7 Estimated position of moving platform

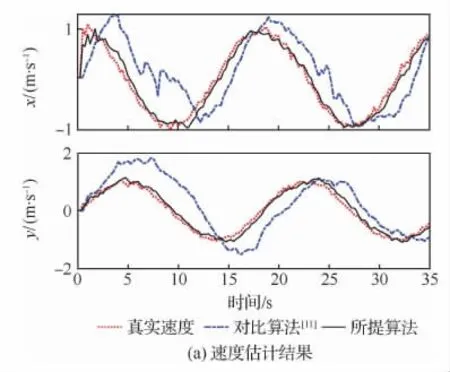
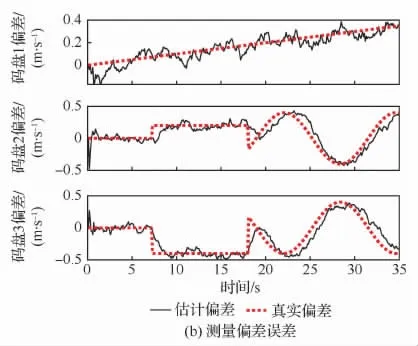
图8 动平台速度估计结果Fig.8 Estimated speed of moving platform

图7 （a）为动平台位置估计结果，图中红色虚线为动平台真实轨迹，绿色标记为视觉定位轨迹，蓝色虚线为对比算法估计结果，黑色实线为所提算法估计结果，从图中可以看到所提算法能较好地估计出动平台的移动轨迹而对比算法则出现较大的偏差。图7（b）中给出了位置估计误差曲线，可以看到所提算法位置估计误差均在0.5m以内，而对比算法估计误差曲线存在较大的波动。

图8（a）中给出了动平台速度估计结果，图中红色虚线为动平台真实速度。蓝色点划线为对比算法估计结果，其存在较大滞后和误差。黑色实现为所提算法估计结果，可以看在码盘存在测量偏差的情况下所提算法仍能较好地估计动平台运动速度。图8（b）给出了码盘测量偏差估计结果，图中点划线为仿真添加测量偏差，实线为所提算法估计测量偏差，可以看到所提算法能较好地估计出码盘测量偏差。

4.3 动平台降落实验

为验证所提降落策略和降落轨迹规划算法，本文设计了动平台处于直线运动和圆周运动下的飞行器实际降落实验，实验中使用文献［21］所提二维码阵列定位系统为飞行器提供精确定位数据，相关实验参数如表1所示。图9和图10给出了降落实验结果，两实验中动平台移动速度矢量模值均为0.35m／s，其中圆形轨迹半径为2.0m。

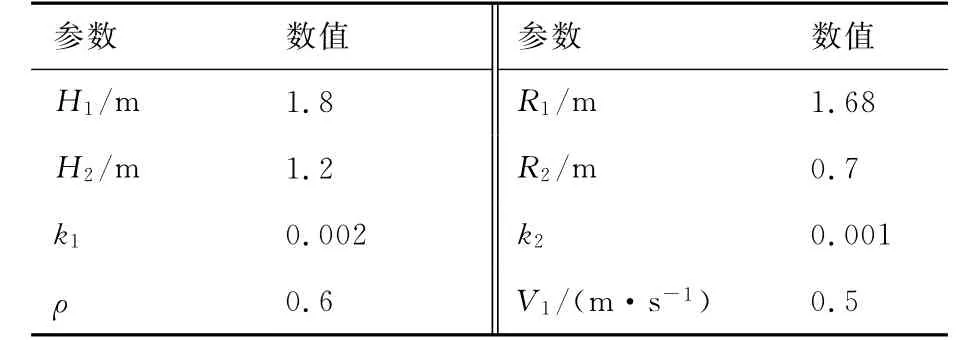
表1 降落规划实验参数Table 1 Parameters of landing experiment

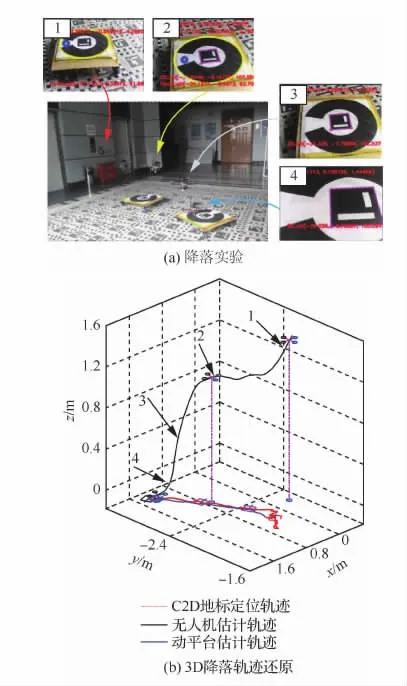
图9 直线轨迹降落实验结果Fig.9 Experimental results of linear motion landing

图9 （a）为动平台进行直线轨迹移动下的降落结果，在图9（a）中1处动平台首次识别目标后初始化状态估计器，在图9（a）中2处飞行器从图像跟踪切换到轨迹规划模式，在图9（a）中3处进行降落轨迹规划，最终在图9（a）中4处飞行器持续进行降落轨迹规划直到降落成功。图9（b）为降落3D轨迹还原图，可以看到动平台估计轨迹符合其直线运动。图10为动平台进行圆形轨迹移动下的降落结果，从3D轨迹还原图中可以看到动平台估计运动轨迹符合所设定的圆形轨迹运动。

图11为动平台受墙壁阻碍导致车轮打滑的实验结果，从图中可以看到由于打滑造成其受阻碍时码盘仍有速度测量值，如直接使用该测量值对动平台速度和位置进行预测将造成较大误差。从图中可以看出各码盘偏差估计值几乎趋近于码盘测量值，因此基于所提运动模型可以保证状态预测时机体速度趋近于零，符合动平台受阻的实际情况。

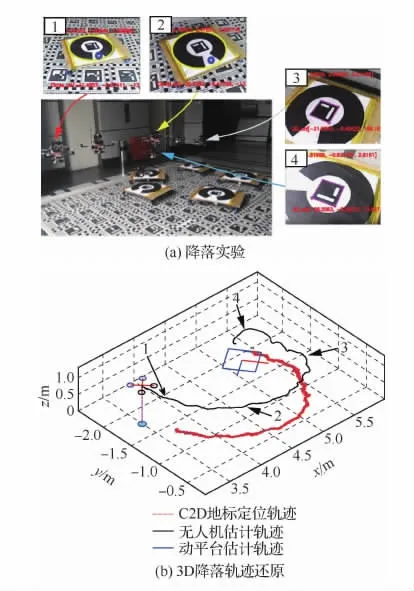
图10 圆形轨迹降落实验结果Fig.10 Experimental results of circular motion landing

图11 动平台车轮打滑实验结果Fig.11 Experimental results of wheel-slip

5 结 论

本文设计了一个基于复合地标导航的优化降落系统，其采用圆环和二维码构成复合地标实现对机载相机的精确定位，基于状态估计理论来估计动平台实时位姿并进一步规划降落轨迹实现飞行器的可靠降落，通过实验验证可以得出如下结论：

1）复合地标结构提高了地标定位的有效范围、降低了定位死区，最终实现相机距离在0.5～6.0m内的综合完整定位并具有最高0.1m的定位精度。

2）所提状态估计算法考虑了码盘未知测量偏差提高了系统在车轮打滑或码盘不精确标定时的位姿估计精度，位置估计误差控制在0.5m内并能为降落规划器提供动平台精确连续的速度估计值。

3）降落轨迹依据飞行器和动平台实时位姿估计值进行在线动态规划，以最小化轨迹Jerk为目标达到了高效、可靠的降落性能，完成了动平台处于直线和圆周运动下的降落任务。