基于高斯混合模型的航迹抗差关联算法

李保珠，董云龙，丁昊，关键

海军航空大学 信息融合研究所，烟台 264001

在分布式多雷达信息融合系统中，航迹关联是信息融合的一项关键技术，旨在确定哪些局部航迹源于同一目标［1］。当雷达存在不完全相同的监视区域、漏探、随机虚警时，造成雷达上报目标不完全一致，导致在另一雷达上报的航迹集合中不存在对应航迹，使得原本复杂的航迹关联问题难度增大。此外，系统误差普遍存在于雷达探测过程中，且受到多种因素影响，造成目标的位置状态估计与真实目标位置之间存在偏差［2－4］，使得传统的航迹关联算法性能恶化严重。

为解决系统误差下雷达航迹关联问题，文献［5-8］利用目标的相对位置信息，提出了基于目标参照拓扑的航迹关联算法，此类算法认为目标间的相对位置关系不受系统误差的影响，但未考虑坐标系的转换中系统误差随目标与雷达的相对位置变化，且无法在理论上给出关联门限。Mori等［9］在目标运动特性的基础上综合利用目标属性特征信息，提出了基于辅助特征的航迹关联算法。文献［10］基于等价量测一阶泰勒展开推导出全局直角坐标系下目标状态估计分解方程。文献［11-12］在此基础上利用真实状态对消得到目标间的航迹矢量，采用航迹矢量检验算法实现雷达目标航迹抗差关联。此外，由于航迹关联与误差配准相互耦合［13］，使得关联和配准的联合求解成为一种新的解决策略。文献［14］将系统误差引入到原始的雷达量测中，构建了一种混合整数非线性规划模型，并对系统误差进行了估计。文献［15］采用多初始点局部搜索的方法，寻找最优系统误差估计值，联合解决航迹关联和雷达误差配准问题。文献［16］采用K-best方法进行航迹关联，同时采用最大似然估计的方法求解系统误差。基于图像匹配的航迹关联算法［17－20］在一定程度上解决了航迹关联问题，成为一种新的航迹抗差关联算法。

受图像匹配中点模式匹配模型的启发，本文将非刚性点集匹配理论引入到雷达航迹抗差关联中，提出了一种基于高斯混合模型的航迹抗差关联算法，首先推导了系统误差下目标测量方程，利用非刚性变换表征航迹集合间的位置关系；其次采用高斯混合模型与航迹间拓扑信息相结合的方法，建立对非同源航迹具有鲁棒性的高斯混合模型，根据航迹间的邻域拓扑信息决定高斯混合模型中各高斯组成部分的初始权重；接着利用期望最大值（EM）算法求解高斯混合模型的最优闭合解，在期望步（E-step）阶段求解航迹的对应关系的概率分布，在最大化步（M-step）阶段求解非同源航迹比例，然后通过航迹关联判决以获得关联结果，最后通过仿真验证各种场景下算法的有效性和鲁棒性。

1 问题描述

图1为某时刻雷达及目标位置分布图，以雷达A为原点建立全局直角坐标系，设雷达A、B的位置坐标分别为 （0，0）、（xB，0），目标T 分别为雷达A、B探测到的第i、j个目标。图中TAi、TBj分别表示目标T相对于雷达A、B的量测位置。由于雷达在探测过程中存在系统误差和随机误差，雷达测量与目标的真实距离、方位角存在偏差。雷达A对目标T的量测为

图1 雷达及目标分布Fig.1 Location of radars and targets

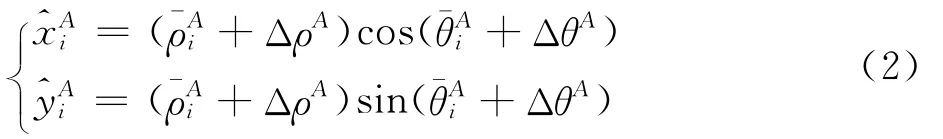
同理，在雷达B处有

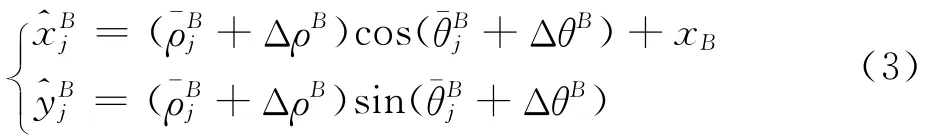
若两航迹源于同一目标（珚x，珔y），则

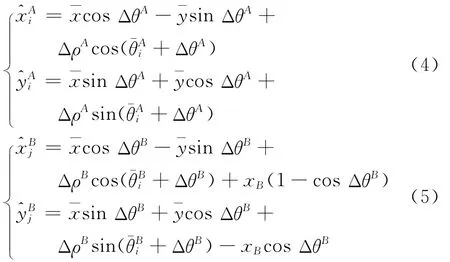
令θ0＝ΔθA－ΔθB，由式（4）和式（5）得

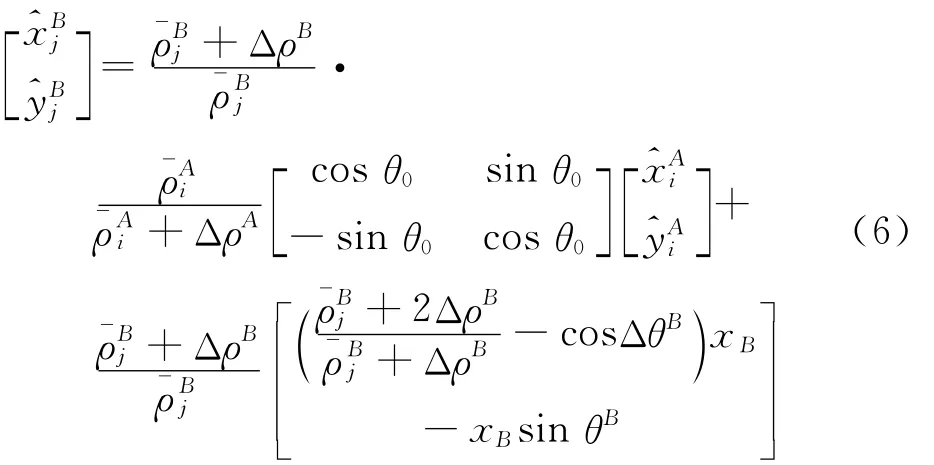
在雷达远距离探测情况下，由于目标相对于雷达的距离远大于测距系统误差，ΔρA和ΔρB可忽略不计，则式（6）为

由式（7）可知，当测距系统误差较小时，雷达A、B对同一目标的位置量测可通过刚性变换（旋转和平移）进行描述；然而，由式（6）可知，较大的测距系统误差不仅使得两组航迹位置信息存在旋转和平移，还造成目标航迹发生非刚性变换，使航迹发生一定程度的整体变形。在分布式雷达监视环境中，探测距离远、系统误差时变、上报目标不一致等复杂因素，使得传统航迹关联算法不再适用，航迹正确关联率严重下降，需要进一步研究适用于上述复杂环境的航迹抗差关联算法。

2 算法描述

2.1 航迹的邻域特征

一般来说，源于同一目标的两条航迹具有相似的邻域特征，因此可根据目标航迹的邻域拓扑信息判断其对应关系。本文采用最优次模式分配（Optimal SubPattern Assignment，OSPA）距离［21］对目标航迹邻域信息的差异进行度量。在全局直角坐标系下，分别为雷达A 和B 上报的航迹集合，＝分别为雷达A、B对目标航迹i、j的状态估计，M 和N 分别为雷达A、B上报的航迹数。根据欧式距离，分别选择目标航迹i、j的K个最近邻航迹构建邻域集合。若目标航迹i和j 源于同一目标，则邻域集合存在一定的相似性。在此，本文采用欧式距离分别对目标航迹的 邻 域 特 征｝进行描述。由于航迹集合中存在非同源目标航迹，因此在集合IAi中选择l个元素构成子集进行相似性度量。定义目标航迹i、j邻域信息相似性度量为

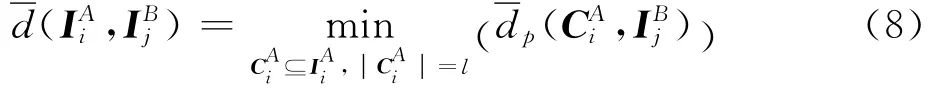
式中：OSPA距离定义为

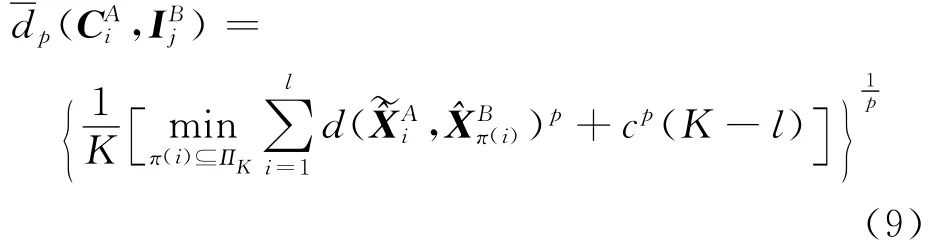
目标航迹的相似性测度可表示为

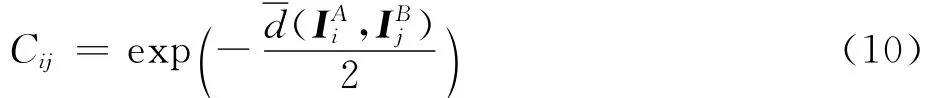
当两目标航迹邻域特征越相似时，目标航迹的相似性测度越大，其航迹源于同一目标的可能性越大。

2.2 高斯混合模型的建立

由于刚性变换是非刚性变化的特殊情况，所以雷达A、B对同一目标的位置量测可通过非刚性变换进行描述。因此，本文将非刚性点集匹配理论引入到雷达航迹关联中，采用具有较强鲁棒性的高斯混合模型（GMM）进行点集的非刚性匹配。将航迹集合XB看作GMM中高斯模型的质心，XA看作GMM产生的样本点集，使得GMM的质心按照一定的邻域拓扑结构整体向样本点集移动。质心与样本点越近，说明航迹点匹配的概率越大。当达到最佳匹配状态时，通过后验概率即可获得航迹集合的对应关系。因此，样本点和质心之间的高斯径向基函数为

式中：D为目标状态估计的维度；σ2为高斯函数协方差。由于雷达上报目标不一致，航迹集合存在非同源航迹，且目标位置状态估计存在过程噪声，因此引入一个均匀分布：

则目标航迹＾XAi的GMM概率密度函数为

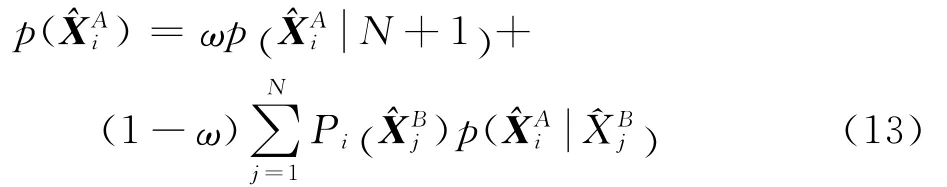
式中：ω为均匀分布的权重系数。由于航迹目标邻域拓扑结构越相似，其源于同一目标的可能性越大，因此在GMM中对应高斯组成部分的权重越大，则定义各高斯组成部分的权重概率为

根据GMM概率密度函数参数估计原理，通过极大似然估计解算GMM参数集合，即最大化对数似然函数：

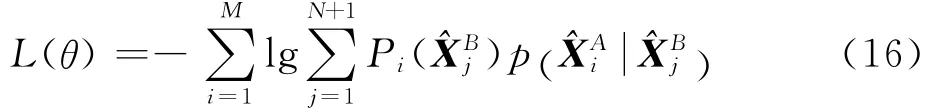
在非刚性点集匹配中，点集集合间的变换关系［22］可表示为

式中：v（XB）为位移函数，为使航迹集合间的变换更加平滑，本文引入一个正则项［22］，使航迹集合保持运动一致性进行整体移动。因此，在再生核希尔伯特空间引入正则化函数。根据文献［22］，式（16）关于参数集合与样本点集的数学期望为

其中：β为平滑性系数。点集集合间的变换关系可表示为XA＝XB＋GW ，并代入式（18）得

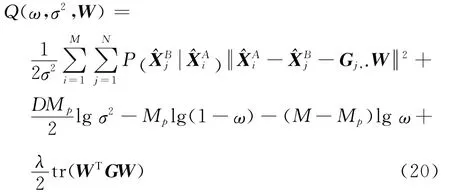
式中：Gj，·为高斯核矩阵的行向量。

2.3 基于EM算法的航迹关联

为求解式（20）中的参数ρ＝ （ω，σ2，W），本文采用EM算法。EM算法实质是利用迭代的方法求解参数集合：

1）E-步：EL（ρ，ρ（k））＝Q

2）M－步：ρ（k＋1）＝ max EL（ρ，ρ（k））

其中：k为第k次迭代运算。通过上述两步的不断迭代，直至收敛得到式（20）的最优解。

2.3.1 E-步

利用参数赋初始值，通过贝叶斯定理［23］计算后验概率为

2.3.2 M-步

式中：1为全1列向量；I为单位矩阵。同理，解Q／σ2＝0，Q／ω＝0可得

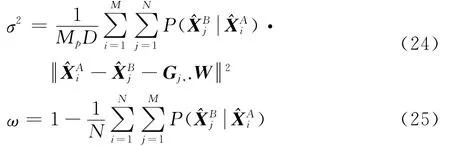
由于在航迹关联中非同源航迹比例ω未知，当ω较大时，式（25）在更新过程中存在过拟合现象，为此，本文采用序贯积累，更新得到修正的ω为

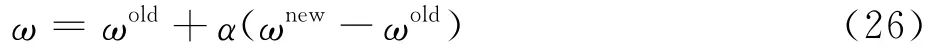
式中：ωold为历史迭代解算的ω值；ωnew为式（25）解算得到的ω值；α＝1／k为学习速度。随着迭代次数k的增加，ω迭代更新速度放慢，有效避免了过拟合问题。因此，非同源航迹的比例ω可通过式（25）和式（26）联合求解。

最后，定义二进制航迹关联矩阵C（i，j）（i＝1，2，…，M；j＝1，2，…，N ）。若雷达A 上报目标航迹i和雷达B上报目标航迹j源于同一目标，则满足：

3 实验结果与分析

3.1 仿真环境

为验证在系统误差时变、上报目标不完全一致等复杂场景下算法的有效性，对本文算法和经典的基于参照拓扑特征的航迹关联（REP）算法［7］及基于傅里叶变换的航迹对准关联（FFT）算法［17］进行仿真实验对比。仿真环境如下：在全局直角坐标系中，两雷达的位置坐标为（0，0）和（150，0）km，有N＝20批目标在区域［72km，75km］×［72km，75km］中均匀分布，目标初始速度服从均匀分布且匀速运动，vo～U（5m／s，200m／s），目标的初始航向均匀分布在［0，2π］范围内，两雷达的量测误差标准差分别为σAρ＝60m，σAθ＝0.4°，σBρ＝80m，σBθ＝0.3°，雷达系统误差缓变，且均匀分布在0到误差上限的范围内，雷达的系统误差上限分别为ΔρA＝1 000m，ΔθA＝－1°，ΔρB＝1 000m，ΔθB＝1°，雷达采样周期为2s，目标跟踪周期数为T＝100，雷达的探测概率分别为PA＝0.9，PB＝0.7。在仿真初始化中，λ＝2，β＝2。为对比算法的关联性能，本文采用平均正确关联率作为评价指标［8］，即实验结果由100次蒙特卡罗仿真求均值得到正确关联的目标数与同源航迹数的比值。图2为目标真实航迹及雷达上报的目标航迹图。

3.2 仿真结果分析

图3为某时刻航迹关联前后的对比图，通过关联前后对比可以看出，当雷达存在系统误差时变、上报目标不完全一致的情况下，所提算法能够有效进行航迹抗差关联。

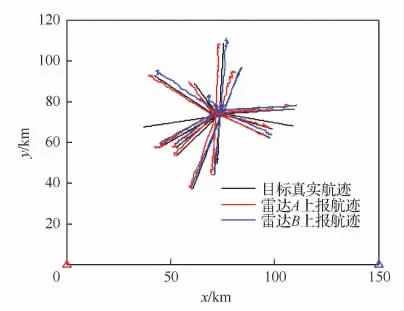
图2 雷达上报目标航迹Fig.2 Target tracks reported by radar

图3 某时刻航迹关联前后的对比Fig.3 Tracks before and after association at moment

图4 为不同测角系统误差下所提算法性能对比图，在仿真过程中只改变雷达测角系统误差，测角系统误差上限在0°～2°等间隔变化，其他参数不变。由图可知，随着测角系统误差的不断增大，FFT算法的平均正确关联率明显下降，所提算法和REP算法性能相对稳定，且所提算法正确关联率达到0.9左右。图5为不同测距系统误差下所提算法性能对比图，在仿真过程中只改变雷达测距系统误差，测距系统误差上限在0～2km等间隔变化，其他参数不变。由图5可知，所提算法与REP算法性能较好。

通过图4和图5可知，随着系统误差的增大，所提算法与REP算法性能相对稳定，且所提算法性能略优于REP算法。FFT算法通过不断地估计航迹间的旋转和平移量进行补差，忽视了非同源航迹的影响，当系统误差较大时，目标位置偏差变化较大，造成与非同源航迹错误关联。REP算法以目标相对位置关系为关联依据，在局部坐标系下，系统误差对目标相对位置关系影响较小，系统误差对REP算法的关联性能影响较小。所提算法在考虑航迹集合整体位置变换关系时，还考虑到目标间相对邻域拓扑信息与非同源航迹的比例，能更好地抵消系统误差对航迹关联的影响。

图4 不同测角系统误差下算法性能Fig.4 Algorithms performance via different azimuth biases

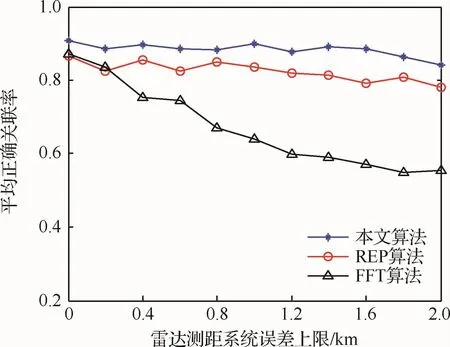
图5 不同测距系统误差下算法性能Fig.5 Algorithms performance via different range biases

图6 为不同探测概率下所提算法性能对比图，在仿真过程中只改变雷达探测概率，探测概率在0.55～1.00等间隔变化，其他参数不变。由图6可知，随着雷达探测概率的不断增大，在目标数量一定的场景下，雷达上报的航迹中存在的共同观测目标不断增多，使得FFT算法受到非同源航迹影响变小，平均正确关联率明显提高。所提算法与REP算法以航迹集合与目标间相对位置关系的相似性为判断依据，综合利用航迹集合与局部拓扑邻域信息，对非同源航迹的鲁棒性较强，特别是所提算法实时估计非同源航迹比例，更加有效抵消非同源航迹的干扰。因此，雷达探测概率对所提算法与REP算法影响较小，随着探测概率增加，平均正确关联率逐步升高且趋于稳定。所提算法平均正确关联率上升至0.9以上，性能优于REP算法。

图7为不同目标分布密度下所提算法性能对比图，保持目标分布区域大小不变，仿真场景中目标数量在15～50逐步增加。可以看出，随着目标数量的增加，FFT算法的关联性能明显降低，REP算法虽然性能良好，但正确关联率缓慢降低，而所提算法相对稳定，平均正确关联保持在0.9左右。因为，随着目标密集程度的增大，非同源航迹增多且相对密集，能达到同源航迹间的拓扑关系，且非同源航迹增多，致使FFT算法与REP算法性能下降，而所提算法通过航迹间相对邻域拓扑信息及自适应的统计门限进行航迹关联的判决，且实时估计非同源航迹的比例，降低非同源航迹对航迹关联的影响。

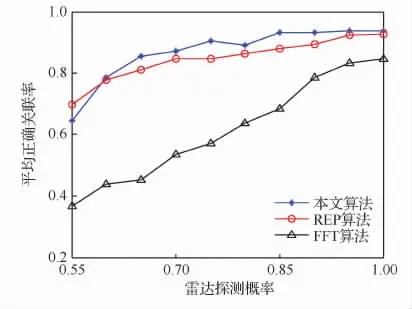
图6 不同探测概率下算法性能Fig.6 Algorithms performance via different detection probabilities

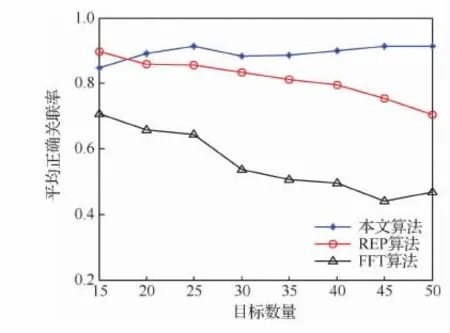
图7 不同目标数量分布密度下算法性能Fig.7 Algorithms performance via the total number of targets

图8 雷达系统误差的均方根误差Fig.8 RMSE of radar sensors bias

图8 为雷达系统误差的均方根误差对比图。由图可知，所提算法对雷达系统误差的估计精度明显优于REP算法和FFT算法。当测角系统误差为2°时，所提算法的平均估计偏差小于0.08°，所提算法测角系统误差的估计精度较高。在估计测距系统误差时，3种算法对测距系统的估计精度一般，但所提算法的估计精度优于REP算法和FFT算法。随着系统误差的增加，算法对系统误差的估计精度逐步降低。这由于FFT算法易受非同源航迹的干扰，造成错误关联。REP算法通过目标间的相对位置关系进行寻优，而忽略了航迹集合的整体配对。所提算法通过迭代寻优，获得较为精确的航迹偏差。因此，所提算法优于REP算法和FFT算法。

图9为本文算法参数λ、β对关联性能的影响。在仿真过程中，正则项权重系数λ在0.1～8内等间隔变化，平滑性系数β在0.1～5内等间隔变化。可以看出，随着λ的增大，本文所提算法平均正确关联率略微降低且趋于平稳；当β≤1.5时，随着β的增大，本文所提算法平均正确关联率略微上升；当β≥1.5时，平均正确关联率随着β的增大而缓慢增大，同时在λ逐步增大过程中趋于稳定。虽然λ，β的取值对算法性能有所影响，但变化浮动相对较小。所以，当0.1≤λ≤5且1.5≤β≤4时，对应的航迹关联性能达到最优化，且λ、β的对算法影响较小。

为验证算法的实时性，本文基于如下配置进行仿真实验：操作系统为 Windows 7；CPU为Intel（R）Core（TM）i7-4790CPU ＠3.60GHz；RAM为8GB。由表1的运行时间对比可以看出，随着目标数目的增加，各算法平均运行时间逐渐增加。FFT算法利用匹配矩阵和目标位置不断交替迭代，REP算法通过计算OSPA距离进行匹配矩阵的求解，两经典算法用时均较小。本文算法每次进行航迹关联时，EM算法估计过程需要进行不断迭代更新，算法运行时间相对较长。

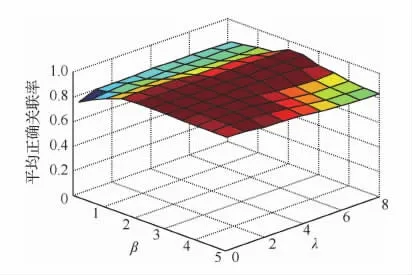
图9 不同λ、β下算法性能Fig.9 Algorithms performance via differentλ，β

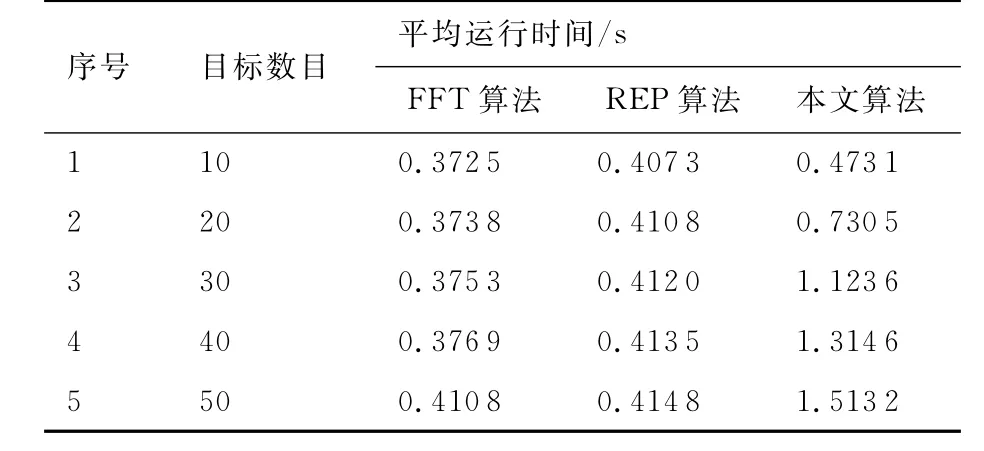
表1 算法平均运行时间Table 1 Average running time of algorithm

4 结 论

1）针对系统误差条件下的航迹关联问题，推导了系统误差下目标测量方程，利用非刚性变换表征航迹集合间的位置关系。

2）本文将非刚性点集匹配理论引入到雷达航迹关联中，建立对非同源航迹具有鲁棒性的高斯混合模型，在不同系统误差、目标分布密度、探测概率等环境下具有较好有效性和鲁棒性，明显优于传统算法。

3）虽然在系统误差条件下关联性能较好，但算法的实时性有待于改善，这主要是因为在算法进行EM迭代寻优过程中具有一定的复杂性，这也将是下一步工作重点。