基于限定记忆加权的辅雷达时变系统误差估计方法∗
(海军航空大学 烟台 264001)
1 引言
雷达组网利用多部雷达之间的信息互联、对比判决,有效克服单一雷达信息获取的局限,实现不同情报的相互共享以及更精确地对目标的参数特征进行估计识别[1]。但组网雷达中系统误差的存在是制约信息融合效用的重要因素。对此,雷达误差配准问题得到了广泛的研究,传统方法主要可以分为三类:1)离线估计方法,如最小二乘(LS)类[2]、极大似然(EML)类算法;2)实时估计方法[3~4],如卡尔曼滤波类算法;3)联合估计算法,如扩维类[5~6],双阶算法等[7~8]。以上算法都主要针对固定系统误差的估计与修正。
在现实环境中,雷达系统误差往往事先无法得知或不准确,或受海域环境多变以及雷达本身机械损耗影响,系统误差在海域内的分布情况极易发生变化。而传统方法在系统误差未知、时变时难以准确跟踪目标航迹。对此,文献[9]提出针对量测误差变化进行建模的方法进行误差修正,但误差变化的多样性是否能完全利用模型代替仍有待验证。文献[10]提出利用mean-shift进行动态误差估计,但对量测样本要求较高,工程实现较为困难。文献[11]提出利用反比例函数进行变误差估计,但仅对距离误差进行了估计。且当前组网雷达系统误差动态估计时,没有考虑充分利用探测精度高或者已被标校的雷达来实现对组网系统其余雷达的误差辅助估计。
针对系统误差时变时,当前方法难以准确跟踪目标航迹以及发生滤波发散的问题,本文以探测精度高的中心雷达为参照,将限定记忆指数加权方法与次优极大后验(Maximum A Posterior,MAP)估值器[12]相结合,提出一种基于限定记忆MAP估值器的辅助雷达自适应EKF误差配准算法。该算法在雷达系统误差未知、时变情况下,能够对辅助雷达系统误差进行有效的实时估计和校准。一方面,该自适应算法相较于现有滤波算法无需提前获知雷达系统误差,且递推校准算法简单,易于现实应用;另一方面,限定记忆加权因子的引入相较于次优常值MAP估值器以及减消记忆MAP估值器精度得到提高,计算时间大大减少。仿真分析及对比实验验证了本文所提算法的有效性和可行性。
2 系统模型与问题描述
设组网雷达由中心雷达与多个辅助雷达组成,其中,中心雷达经过标校设备事先标校,探测精度较高。以此中心雷达为参考,对多辅助雷达的系统误差进行估计。
对于与中心雷达同时探测到一批目标的各辅助雷达i,其观测向量定义为Zi(k)=[ri(k)'θi(k)] ,状态向量为,系统偏差为,则有如下关系式:
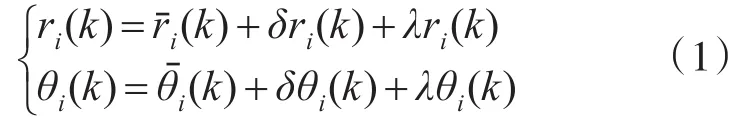
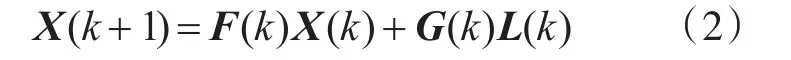
其中,L(k)为白色高斯的随机变量,其方差阵为Q(k),G(k)为过程噪声分布矩阵。
设辅助雷达i相对于中心雷达存在系统误差Δi(k),且 Δi(k)随量测时间的推进发生变化,则辅助雷达i的量测方程为
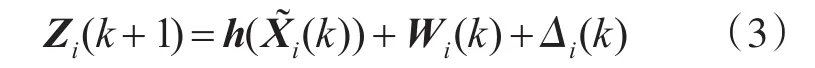
其中,W(k)为白色高斯的随机变量,其方差阵为R(k)。利用扩展卡尔曼滤波实现各辅助雷达的目标状态的估计。

一般来说,对于系统误差估计与修正问题由以下假设:1)同一雷达在某海域的系统误差在很长一段时间内可看作是缓变的;2)不同雷达对于同一海域的系统误差变化情况是不同的。因此,假设中心雷达利用合作目标(GPS、AIS等)实现了精确校准,但多个辅助雷达系统误差未知且海域系统误差时变、分布不明。本文即以中心雷达为参考,实时估计各辅助雷达的系统误差,实现更精准的信息融合。
3 系统误差估计
3.1 恒定系统误差下次优MAP估值器

但对于时变系统误差的估计,距当前时刻较远的陈旧数据会影响时变系统误差估计的更新,使估计值不够准确,进而对后续估计值产生影响,直至产生发散。因此在估计时应着重利用新进数据,逐渐遗忘陈旧数据。对此,可将次优MAP系统误差估计器进行衰减指数加权以实现数据的权重选取。从系统误差变化快慢以及计算耗时的角度出发,给出两种指数加权MAP估计器。
3.2 时变系统误差下渐消记忆指数加权MAP估值器
当时变系统误差变化缓慢时,可以将渐消记忆指数加权应用到MAP估值器中,即对各时刻中心、辅助雷达滤波差值赋予不同的权重系数。加权系数{βj}的选取满足如下公式:

其中,b为遗忘因子,其值视系统误差时变快慢而选择不同值。实际应用中,一般取0.95~0.995。对于b的取值与衰减程度的关系,如图1所示。
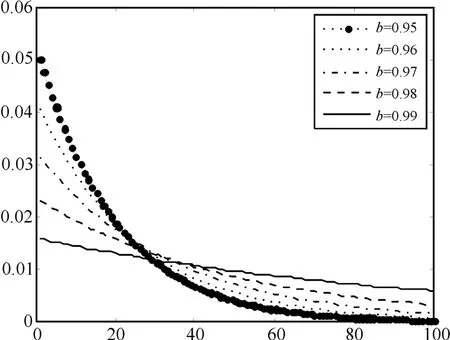
图1 加权系数与遗忘因子数值关系曲线
式(12)中每项滤波差值利用加权系数βk+1-j替换原有权系数1k,即得到渐消记忆时变系统误差MAP估计器:
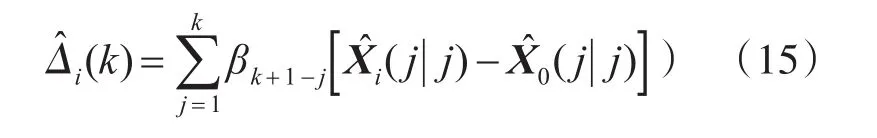
3.3 时变系统误差下限定记忆指数加权MAP估值器
渐消记忆指数加权MAP估值器在对时变系统误差进行处理时,利用了当前时刻过去所有的记忆数据,但数据较当前时刻越陈旧,其所被赋予的权重越小,即对当前系统误差的估计作用越小。当系统误差变化较快或可能产生突变时,过于陈旧的滤波差值数据对当前时刻系统误差的估计参与度很小,由于遗忘因子与加权系数的关系,当雷达采样时间较长时,过于陈旧的滤波差值数据被赋予极小的权重,不仅对当前时刻估计作用不大,且各时刻因频繁、重复的权重因子分配使计算时长增大。因此,一方面,为提高时变系统误差估计精度;另一方面,减小计算时长,只利用当前时刻之前一固定时间段内数据进行误差估计,即将限定指数加权方法应用到MAP估值器中。
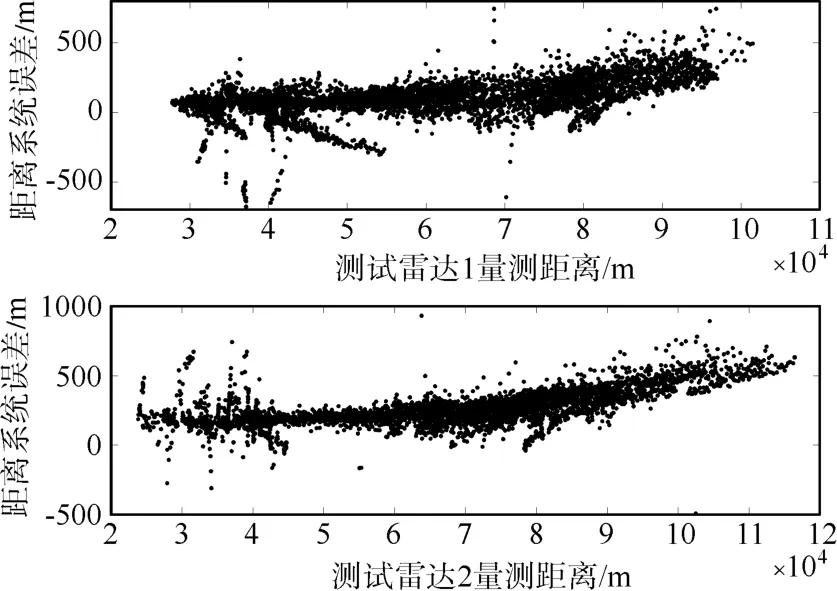
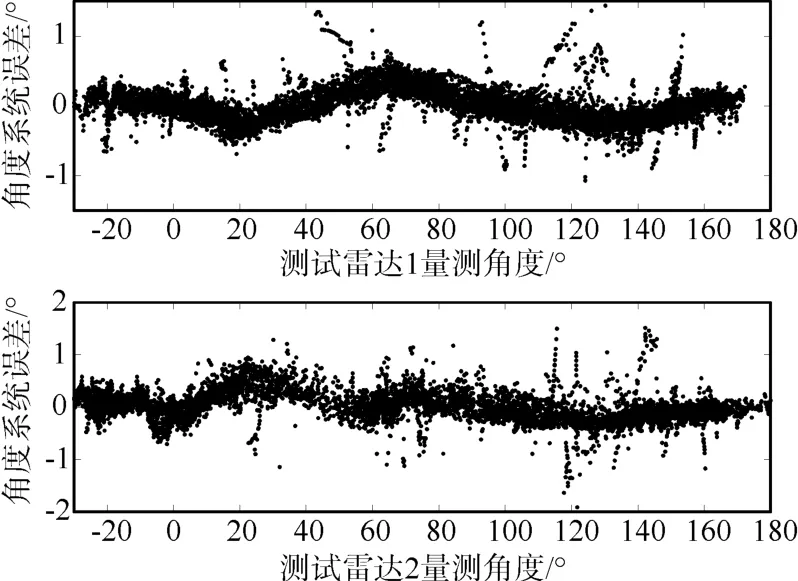
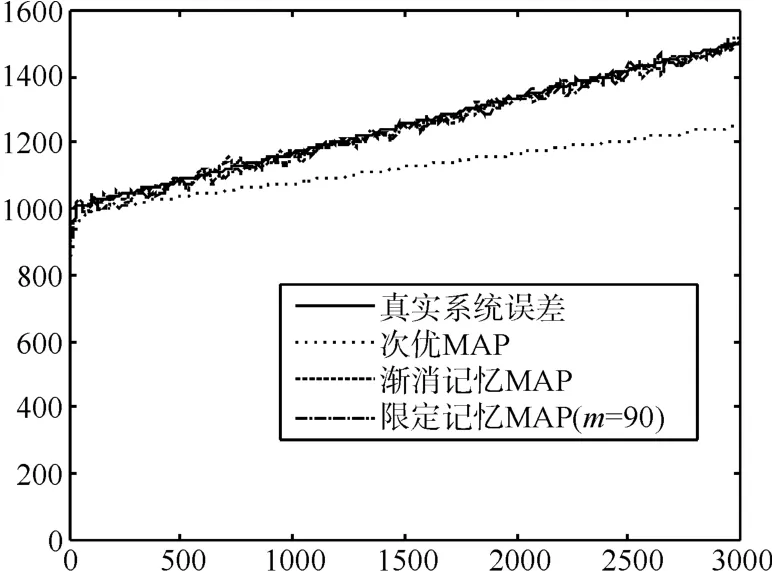
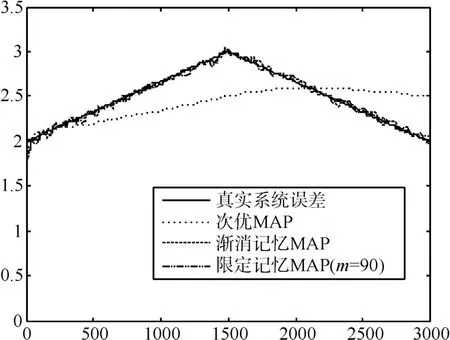
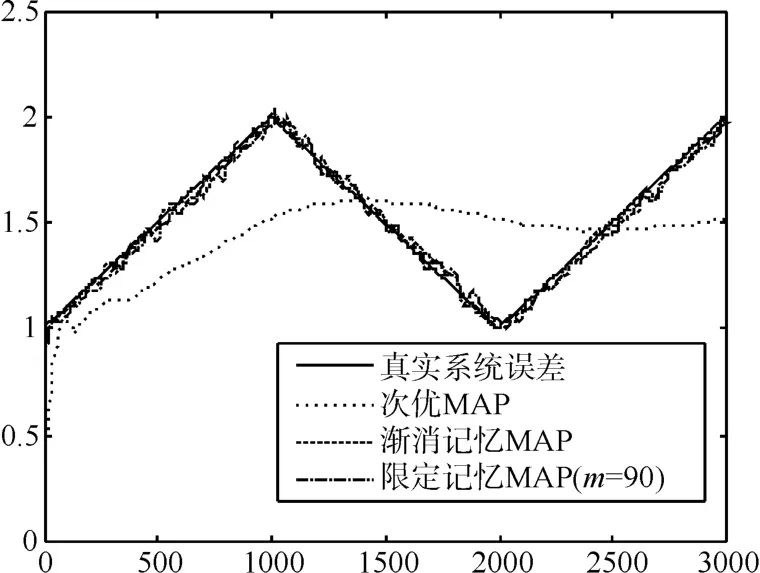
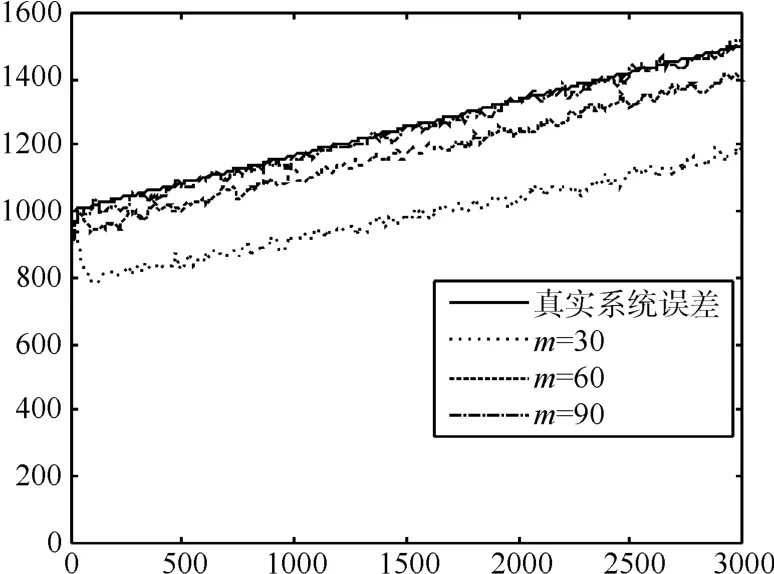
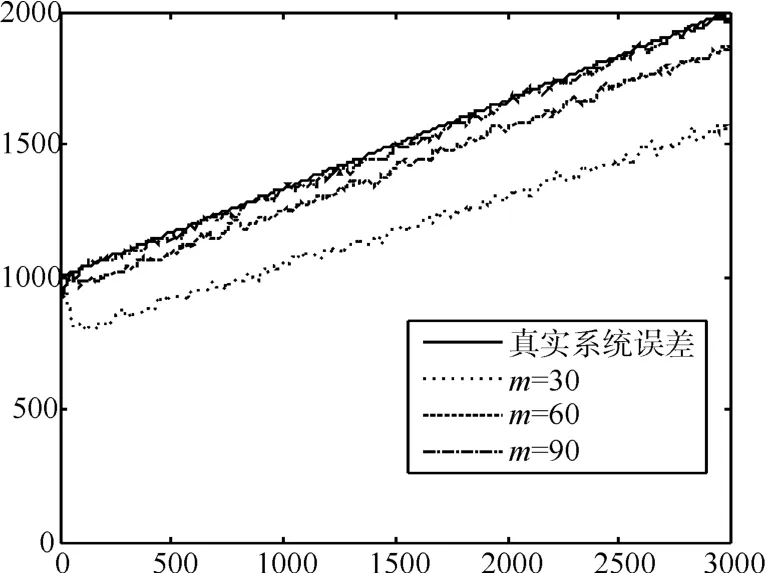
预先设定限定记忆长度为m,且0 其中,b为遗忘因子。将式(12)中k-m时刻之后每项利用加权系数βj+1-m替换原有权系数,即得到限定记忆时变系统误差MAP估计器: 限定记忆时变系统误差MAP估值器的起始递推时刻为k=m+1,因此在计算时需要已知当前时刻之前存储的历史数据。即事先确定m时刻之前初 始 值若m时刻之前初始值无法事先确定,则当k 假设在k时刻,各辅助雷达利用EKF得到各自对目标的状态滤波值,然后利用限定记忆指数加权MAP估值器得到系统误差估计,之后对k+1时刻辅助雷达i的量测数据Zi(k+1)进行修正,对雷达在探测海域内时变系统误差进行实时递推估计和校准。最后,将各雷达修正后航迹上报融合中心,进行数据融合。 图2 限定记忆MAP误差配准方法框架 利用仿真实验进一步说明本文所提误差配准的精确性。考虑如下仿真环境。 假设存在三部岸基对海雷达,其中一部为中心雷达,位于坐标原点,两部为辅助雷达,其中辅助雷达1位置坐标为(u1'v),辅助雷达2位置坐标为(u2'v),其中u1=185200m,u2=55260m,v=0。海面存在一船舶待探测目标,远离海岸方向向东行进,如图3所示,雷达探测过程中均存在雷达扇面横扫过程。 图3 仿真场景示意图 设三部雷达的量测噪声误差均为σr=σr1=σr2=50m ,σθ=σθ1=σθ2=0.2°。 为对变化的系统误差进行准确的仿真,仿真之前利用测试雷达1、2与AIS标校设备对某海域船舶目标进行量测。利用AIS得到的目标精准位置与雷达量测位置的一次差得到雷达的系统误差(量测目的是为探究系统误差大体变化趋势,所以此时忽略量测误差影响)。得到系统误差与其量测向量关系大体如图4、5所示。分析可以看出,距离、角度系统误差与其量测向量总体呈线性关系,但角度系统误差波动性较大。 图4 测试雷达距离系统误差与量测关系 图5 测试雷达角度系统误差与量测关系 基于此实测验证,为简化误差变化模型,现将系统误差设定如下:雷达1距离、角度系统误差,雷达2距离、角度系统误差分别为 其中,n为迭代步数。目标的真实初始状态为(6000'50'50000'-10),迭代步数为n=3000。 图6~9是本文所提限定记忆MAP估值方法(限定长度m=90)与减消记忆MAP估值方法以及次优MAP估值方法进行系统误差实时配准后的对比结果,可以看出,限定记忆MAP估值方法(限定长度m=90)与减消记忆MAP估值方法都可以对时变系统误差进行实时跟踪,但限定记忆方法较减消记忆方法计算时间大大缩减。另外,次优MAP常值系统误差估值方法无法对时变系统误差进行实时估计。 图6 雷达1三种不同方法距离系统误差估计对比 图7 雷达1三种不同方法角度系统误差估计对比 图8 雷达2三种不同方法距离系统误差估计对比 图9 雷达2三种不同方法角度系统误差估计对比 图10~13为限定记忆MAP估值方法在限定长度m取不同值时的误差配准效果,可以看出,当限定长度过小时,一旦系统误差出现估计发散,后续系统误差估计极易受此影响进而产生偏差较大的系统误差估计,因此,在实际应用中,应合理选取m的取值。且由实验可知,当m取值大于90时,限定记忆方法即可达到与减消记忆方法相近的效果,这相较于减消记忆方法动辄近千的权重因子计算分配大大降低了计算量。 图10 雷达1距离系统误差不同限定长度误差估计 图11 雷达1角度系统误差不同限定长度误差估计 图12 雷达2距离系统误差不同限定长度误差估计 图13 雷达2角度系统误差不同限定长度误差估计 对海雷达在对海上目标进行探测时,雷达系统误差在数值上主要有两种可能性:1)误差未知或不准确;2)分布非均匀或时变。而传统误差配准方法在系统误差未知、时变情况下无法对目标状态进行有效识别,甚至由于系统误差估计偏离过大出现滤波发散。对此,本文将限定记忆指数加权方法应用到次优极大后验估值器(MAP)中。充分利用组网系统中中心雷达高精度优势,设计了一种基于自适应EKF滤波算法的时变系统误差估计器。用以对辅助雷达的时变系统误差进行实时估计和校准。所提限定记忆MAP估值算法具有以下优势:1)所提递推方法简单灵活,且不附加任何限制条件,易于工程应用;2)能对未知、时变系统误差进行快速、精准估计,且相对于减消记忆方法大大减少了计算量。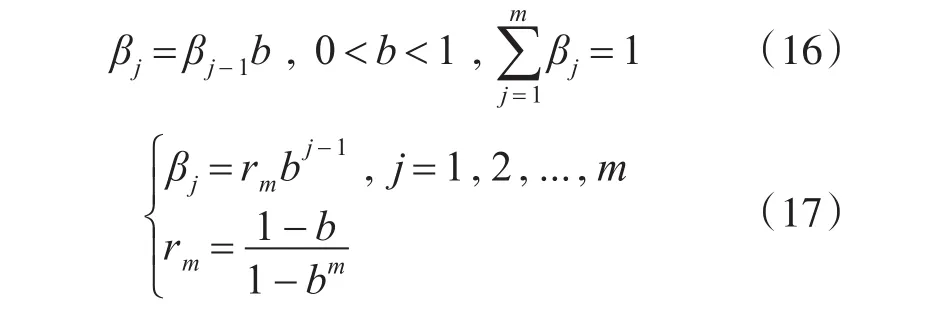

3.4 误差配准框架

4 仿真实验





5 结语

