基于最大序列相关性的Turbo码交织器识别

吴昭军，张立民，＊，钟兆根

1.海军航空大学 信息融合研究所，烟台 264001 2.海军航空大学 航空基础学院，烟台 264001

为了对抗恶劣的信道环境，现代数字通信系统广泛采用信道编码的方案，通过增加码元之间的冗余信息，从而实现信息码元的自动检错与纠错。Turbo码是目前信道编码中一类性能较好的编码方案，现在广泛应用于卫星通信、深空探测等领域［1］。对于非协作通信而言，Turbo码中随机交织器的识别是Turbo码识别的重要内容之一［2］，能给后续盲译码提供必不可少的先验信息。

目前，大部分算法集中于完成Turbo码分量编码器识别［3－6］，而单独针对交织器识别的算法较少，大多数局限于实现交织帧长度［7－9］或是仅针对卷积交织［10－11］、分组交织［12］这样固定结构的参数识别。从已有的文献来看，主要分为两个大类，即：基于硬判决以及基于软判决码元的交织关系识别。文献［13］首先将Turbo码分量编码器展开为冲激响应序列，利用未交织信息序列，脉冲序列以及交织编码序列三者的约束关系逐位验证完成识别，该算法在能够在无误码条件下完成交织关系以及冲激响应序列的同时识别，但是一旦出现误码，算法将会失效；文献［14］从信息熵的角度出发，利用正确的交织位置与错误交织位置上信息码元与编码码元之间约束关系成立的概率不同，将结果以熵的形式来度量，逐位进行验证，从而估计出交织关系，该算法具有一定的容错性能，但是计算量很大，实时性不高；从提高交织器识别算法实时性以及容错性两个方面出发，文献［15］提出了一种高误码条件下的Turbo码交织器恢复方法，该方法主要利用了校验向量的特征，仅仅依赖几个相关位置进行识别，避免了误码的累积，但是当交织长度增加时，算法性能将会急剧恶化，需要截获大量的数据帧块，才能改善；为了提高Turbo码交织器在低信噪比下识别的可靠性，同时为了将有限域中交织器识别算法推广到信号处理方式丰富的实数域中；文献［16］利用Turbo码译码器软输出之间相关性，提出了一种迭代估计算法。该方法虽然克服了硬判决算法容错性能低的缺点，但是在迭代估计过程中算法的复杂度非常高；从提高实时性角度出发；文献［17］提出了基于校验方程符合度下的Turbo码交织器识别方法，该方法直接利用了软判决信息，通过遍历交织位置，求取最大的校验符合度完成交织关系识别，该算法具有较好的低信噪比适应能力，但是当交织长度过长时，算法的性能会急剧恶化；文献［18］为了进一步减少计算复杂度，提出低信噪比下，基于对数符合度的随机交织器识别算法，该算法在计算对数符合的方法上更加简单，与文献［17］一样，随着交织长度的增加，误差将会累计；为克服现有算法性能随交织长度增加而急剧恶化的缺点，文献［19］提出了基于Gibss采样下的交织器识别算法，该方法是基于文献［17］的改进，在文献［17］的基础上，利用部分相关数据采用Gibss样本法进行纠错，在一定程度上改善了算法的性能，但是实时性能却减弱了不少。综合上述分析，现有的Turbo交织器算法还存在着容错性与实时性不好的缺点。

鉴于此，本文提出了一种低信噪比条件下，Turbo码随机交织器识别算法，该算法首先利用第3路编码码元对每一帧交织前的信息码元进行重新估计，得到不同数据帧上同一交织位置上的估计序列；其次遍历所有的交织位置，将所估计的序列与同一遍历位置上不同帧块上原始信息序列做互相关运算，则最大的互相关系数所对应的位置即为估计的交织位置。同时在估计过程中，算法利用第2路码元序列对第1路的信息码元进行校正，然后利用第1路码元对第3路已估计完的交织位置上码元进行校正，这样最大程度的克服了以往算法随着交织长度急剧恶化的缺点。仿真结果表明，提出的算法容错性较强，同时计算复杂度适中。

1 Turbo码编码原理以及模型建立

Turbo码自1993年提出以来，广泛应用于通信系统中。Turbo码编码结构主要是以并行级联型为主，图1为并行级联型Turbo码编码、发送、接收示意图。图中：ut为时刻t的信息码元分别为第1路与第2路的分量编码器，通常这两路的分量编码器相等。c1，t与c2，t为第1分量编码器与第2分量编码器的t时刻的输出；xt，yt以及zt分别为时刻t下，ut，c1，t，c2，t经过信道后的软判决输出；π为交织器。设时刻t以内的信息序列可以用多项式表示为

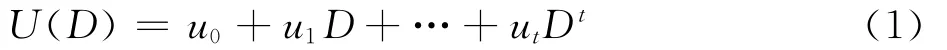
式中：D为延时单元，则

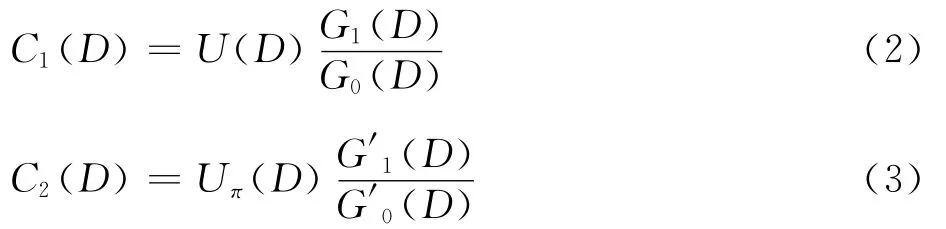
式中：C1（D）为第1路分量编码器编码多项式。

式（3）为第2路分量编码器编码多项式。设分量编码器寄存器个数为m，若以g1，i，g′1，i（0≤i≤m）表示第1与第2路分量编码器前向多项式系数，以g0，i，g′0，i（0≤i≤m）表示第1与第2路分量编码器反馈多项式系数，通常Turbo码中两种分量编码 器是相同 的，故 有 g1，i＝ g′1，i，g0，i＝g′0，i，故将式（2）与式（3）展开后，得到

式中：“⊕”表示二元域中加法运算。

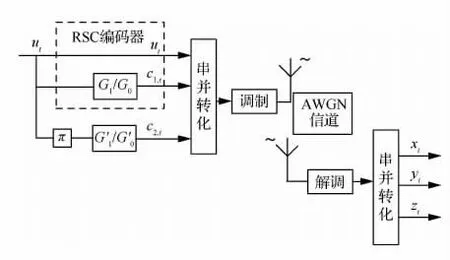
图1 Turbo码编码、发送、接收示意图Fig.1 Turbo code of encoding，sending，and receiving

由于截获的码元xt与yt是未经过交织的码元编码输出，利用现有的算法能够高效的完成分量编码器的识别，同时文献［9］首先将截获的码元做差分预处理，利用每一帧初始位置两码元之间的差分结果一定为零的特点，构建差分序列分析矩阵，实现了在误码率高达0.2条件下码长以及帧同步的可靠识别，所以本文假定分量编码器以及码长已经完成了估计，重点研究低信噪比下利用分量编码器，截获的软判决码元实现交织器π的识别。

2 低信噪比下交织器识别模型

参数估计的基本思路为：利用截获的软判决序列以及生成多项式G1（D）／G0（D）首先对每一帧数据交织位置上的信息码元进行预估计，得到不同数据帧同一交织位置上的估计序列，然后遍历交织位置，将所估计的序列与同一遍历位置上不同帧块原始信息序列做互相关运算，则最大的互相关位置即为估计的交织位置。

2.1 交织位置信息序列估计

在整个交织器识别过程中，信息序列的正确估计是关键。下面重点研究如何利用截获的编码序列以及生成多项式完成交织位置信息序列的估计。

由于生成多项式中g1，0＝g0，0＝1，故式（5）可以进一步写为

在第k帧数据中，标记：

则第k帧数据的第t个交织位置码元uk，π（t）取值为0，1的条件概率为

式中：v＝0，1。

利用贝叶斯公式，将式（10）展开，得到

在uk，π（t）＝v确定后，各路码元之间相互独立，仅仅与多项式系数相关，故式（11）进一步转化为

为了进一步化简式（12），引入对数似然比运算，将Pc（uk，π（t）＝v）转化为对数似然比，即：

式中：llr（·）为对数似然比。

当信息序列 Xvk，π（t）以及多项式确定后，每一路码元的概率分布就确定了，各个码元之间可以认为是相互独立，故式（13）可进一步展开为

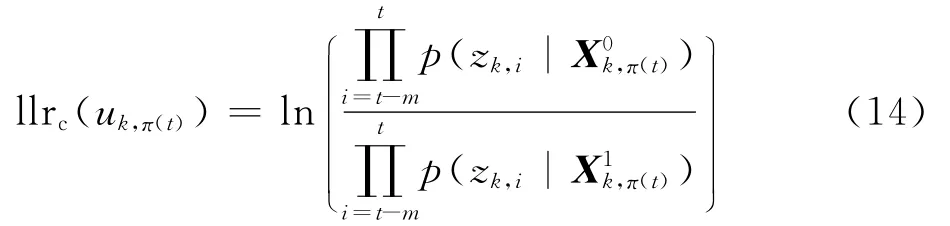
进一步化简为

由式 （7）可 知，序 列 Xvk，π（t）＝ ［v，xk，π（t－1），…xk，π（t－m）］仅仅可以确定时刻t，c2，t的取值，若要确定c2，i，（0≤i＜t）的取值概率，则需要序列［xk，π（i），xk，π（i－1），…，xk，π（i－m）］，而此时v 并不在该序列中，故xk，π（t）的取值对其并无影响，故有

由此，式（15）简化为只需要求取i＝t时的对数似然比值，即

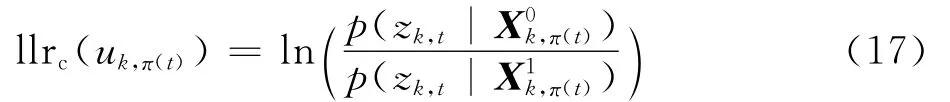
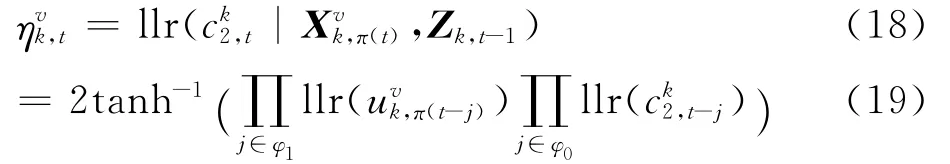
式中：φ1＝ ｛j＝0，1，…，m｜g1，j＝1｝，φ0＝ ｛j＝1，2，…，m｜g0，j＝1｝。

设传输信道为AWGN信道，调制方式为2PSK，载波幅度为A，则

式中：σ2为白噪声方差。

由对数似然比概念，式（18）条件对数似然比可进一步转化为条件概率为

将式（22）以及式（23）代入式（15）可得

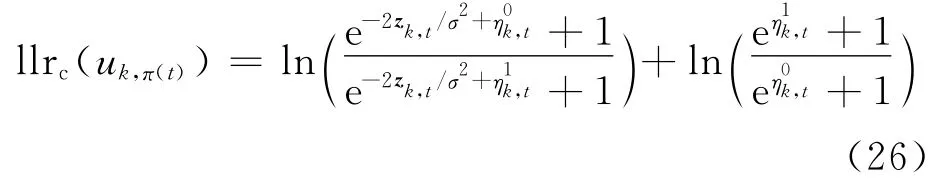
由于ln（ef1＋ef2）≈max（f1，f2），故式（24）可进一步化简为

由式（27）中uk，π（t）的条件 似然比 的求解方法，可以得到每一帧数据交织位置上码元似然比的预值，即

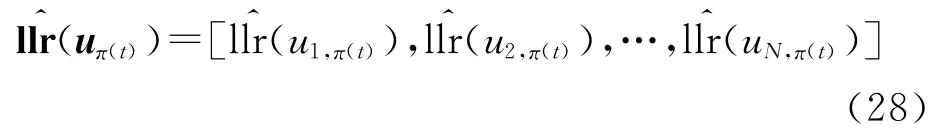
式中：N为截获的帧块数目。

通过遍历可能的交织位置，将所有数据帧上同一位置上的对数似然比序列与预估的序列做相关运算，即

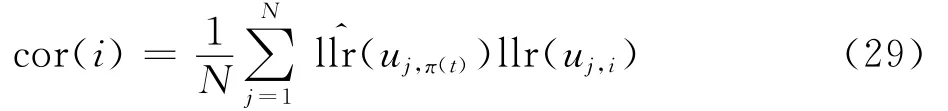
式中：i∈ ｛1，2，…，L｝＼｛π（1），π（2），…，π（t－1）｝。

由于算法对交织关系的估计过程中，需要利用已经估计完的交织位置，随着交织位置的增加，算法的可靠性会降低，为了克服这样的缺点，本文首先利用第2路软判决信息对第1路信息进行增强更新，即利用第2路软判决码元yk，t以及生成多项式系数对第1路中第k帧t时刻的信息码元进行预估计，整个过程与上面基本一致，即

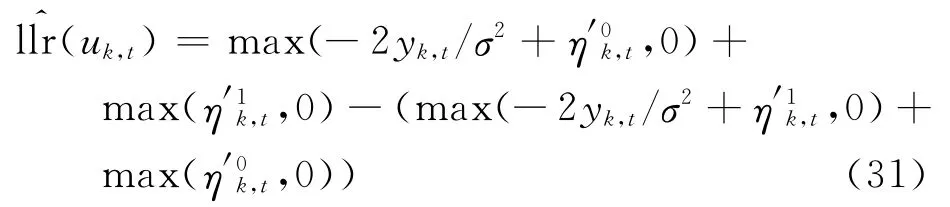
式中：

将预估的值llr＾（uk，t）与第1路码元llr（uk，t）进行叠加，实现第1路码元的更新增强。

同理，利用已经识别的交织位置的信息码元以及生成多项式系数对第3路码元进行校正更新。首先进行预估即

其中：φ1＝ ｛j＝0，1，…，m｜g1，j＝1｝，φ0＝ ｛j＝1，2，…，m｜g0，j＝1｝。

将预估的值llr＾（ck2，t）与第3路码元llr（ck2，t）进行叠加，实现第3路码元的校正增强。

完成一个交织位置的识别，第3路信息序列以及第3路编码序列上相应位置的软判决信息得到更新，直到所有的交织位置完成识别。

2.2 交织关系识别流程

由2.1节中，推导过程可知，Turbo码交织器识别过程主要由2个部分组成，即：估计与校正过程。估计阶段：利用第3路码元以及多项式系数完成对每一帧数据交织位置的信息码元预估计，然后将预估计的序列与每一帧数据上遍历位置的信息序列作相关运算，相关度最高的位置即为交织位置；校正阶段：利用第2路码元信息与多项式系数对第1路码元进行预估计，将估计的信息序列与原信息序列相叠加，完成第1路信息更新，其次利用已经完成识别的第1路交织位置上码元信息以及多项式系数对第3路码元信息进行预估计，将估计的第3路码元序列与原始的第3路码元序列相叠加，完成第3路码元信息的更新。估计与校正两个阶段轮流进行，直到最后一个交织位置识别完成，具体的步骤如下：

步骤1 将截获3路软判决信息转化为对数似然比形式，同时t＝1。

步骤2 利用式（19）以及式（27）计算每一帧第1路交织位置上信息序列的条件对数似然比，获得序列

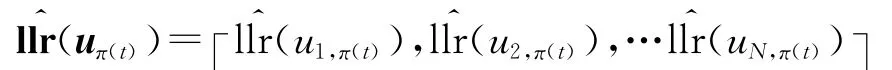
步骤3 遍历原始信息位置i，其中，i∈｛1，2，…，L｝＼｛π（1），π（2），…，π（t－1）｝，将步骤2中的序列与每一帧第一路原始序列同一遍历位置的序列作相关运算，并存储相关运算结cor（i）。

步骤5 利用式（31）以及式（32）计算每一帧第1路数据t位置的估计值

步骤6 利用式（33）以及式（34）计算每一帧第3路数据t位置的估计值

步骤7 将步骤5以及步骤6中的估计值分别与第1路以及第3路每一帧t位置的码元相叠加，完成每一帧第1路与第3路码元相应位置的校正更新，同时t＝t＋1，重复步骤2到步骤7，直到t＞L，输出交织关系π，完成识别。

从算法的流程来看，整个过程分为估计与校正两个部分，步骤2到步骤4是对交织关系估计，步骤5到步骤6是对第1路以及第3路信息序列进行估计，为序列校正准备条件；步骤7是利用估计的序列对原始序列进行校正。提出的算法能够在估计交织位置时实现对第1路以及第3路序列的校正，能够避免以往算法随着交织长度的增加性能急剧恶化的缺点。

对于删余Turbo码而言，主要在于校验方程不同，利用文献［21］可以获得删余条件下RSC码校验多项式，此时利用校验方程，可以对每一路信息的对数符合度进行估计，从而完成交织器识别，原理与不删余一样，不再赘述。

2.3 计算复杂度分析

从算法的步骤来看，设交织长度为L，截获帧块数目为N，编码器寄存器个数为m。当对第t个交织位置进行识别时，算法首先对每一帧交织位置的码元进行估计，需要进行N（2（m＋1）－1）次乘积运算、N次tanh－1（·）运算以及N次比较运算；然后需要遍历（L－t＋1）个可能的交织位置，每遍历一次就需要将不同数据帧上遍历位置的数据序列与估计序列作相关运算，总共需要N（L－t＋1）次乘法运算、N（L－t＋1）加法运算以及L－t＋1次比较运算；在校正过程中，需要对第1路以及第3路序列进行估计，总共需要2 N（2（m＋1）－1）次乘法运算、2 N 次tanh－1（·）运算以及2 N次比较运算；在序列更新过程中，需要2 N次加法运算。设定一次比较运算与1次加法运算相当，一次tanh－1（·）运行等价于4次乘法运算，则整个算法总的乘法运算次数mul以及加法运算次数sum近似为

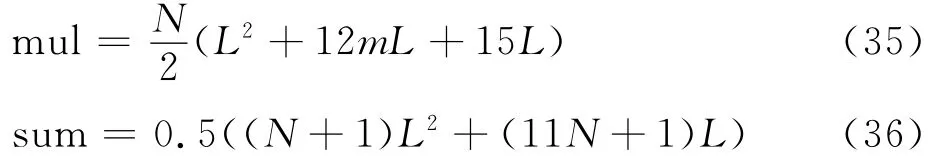
故算法的乘法复杂度为O（NL2），加法复杂度为O（（N＋1）L2）；如果将码长以及帧同步考虑在内，由文献［9］可知，码长的计算复杂度为O（l／r2），其中l为截获的数据量，r为构建的分析矩阵行数，运算 · 为向下取整；帧同步的计算复杂度为O（N），忽略低阶项，本文算法整体计算复杂度约等于O（NL2）；而文献［14］中Cluzeau算法每一步的计算复杂度为O（NL2m），总的计算复杂度为O（NL22m）；文献［17］采用基于平均校验方程符合度的交织器识别算法，总共需要L步，每一步计算复杂度为O（NLm），总的计算复杂度为O（NL2m），而文献［19］算法是文献［17］的改进，在文献［17］的基础上，增加了Gibbs样本法进行纠错，其计算复杂度为O（NL2m＋2 NL（m＋1）m2）。从计算复杂度来看，本文算法要小于Cluzeau算法，而与文献［17］以及文献［19］运算量相当。

3 仿真分析

3.1 算法有效性分析

仿真1 算法正确性验证

选定Turbo码交织长度为1 024，截获的交织帧数为2 000，编码多项式为（7，5）递归系统卷积码，其生成多项式为（1，（1＋D2）／（1＋D＋D2）），设置信噪比为3dB，交织关系为随机交织，在交织映射关系中，π（18）＝15，π（256）＝156，π（512）＝466，π（768）＝556，π（890）＝860，π（1 024）＝287。下面验证算法对以上位置的交织关系进行验证（取其他位置亦可）。首先利用第3路信息以及已识别的交织位置信息对π（18），π（256），π（512），π（768），π（890），π（1 024）上的第1路每一帧码元进行预估，得到如图2（a）所示的结果（为便于观察，这里仅展示π（18）所在位置前200帧估计值，实际应有2 000帧）；其次遍历交织位置，将估计的序列与遍历位置不同帧上的序列作相关运算，得到如图2（b）所示的结果；最后，利用第2路信息对第1路每一帧第18，256，512，768，890以及1 024位置上码元进行估计以及利用第一路已经估计完毕交织位置上的信息对第3路每一帧上述位置的码元进行估计，结果如图2（c）以及图2（d）所示（同样为了便于观测，这里只画出了π（18）前200帧估计位置序列，实际有2 000个）。

首先从得到的结果来看，算法在位置15，156，287，466，556以及860各自取得最大的相关系数为67.69，70.11，70.32，69.59，71.02以及71.21，此时估计的交织关系为＾π（18）＝15，＾π（256）＝ 156，＾π（512）＝ 466，＾π（768）＝ 556，＾π（890）＝860，＾π（1 024）＝287。这与实际设定是一致的，说明算法有效；从估计的序列来看，图2（a），图2（c）以及图2（d）原始信号与估计信息的符号是一致的，此时序列的相关性将是最好的。

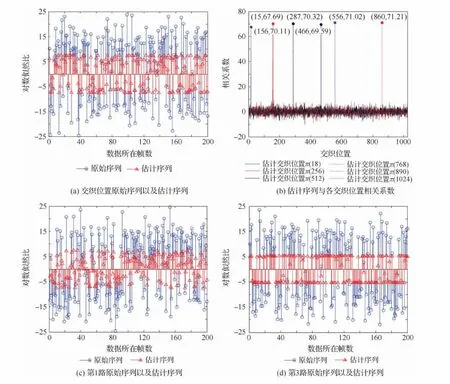
图2 估计的信息序列以及相关运算结果Fig.2 Estimated information sequence and results of correlation operation

仿真2 交织位置相关性与次最大相关性对比

在识别过程中，正确交织位置的序列相关值与次最大序列相关值的差异程度，因为只有当二者的差异程度越大时，识别出的结果可靠性才能越高。设定交织长度为1 000，交织方法为随机交织，多项式参数设定与上面一致，截获码元数目为2 000，信噪比为0dB，记录在交织关系识别中，每一个正确的交织位置上有校正与无校正情况下，相关系数值，以及该两种情况下，次最大的相关系数，结果如图3（a）所示；然后考察在不同信噪比环境下，有校正和无校正两种情况下，正确交织位置的平均相关系数cor以及次最大平均相关系数差异程度，设定信噪比范围为－6到6dB间隔0.5dB取值，记录平均相关系数的结果如图3（b）所示。

图3 有校正与无校正情况下，交织位置相关系数与次最大相关系数对比Fig.3 Comparison of maximum and sub maximum correlation coefficients with correction and without correction

从图3得到的结果来看，在0dB噪声环境下，有校正条件下，交织位置的相关系数与次最大相关系数的差值要远远大于无校正的情况，这说明有校正的交织器识别算法低信噪比适应能力要远远好于无校正的情况；从图3（b）来看，随着信噪比的增加有校正与无校正两种条件下，二者与各自次最大的差值逐渐接近，但是当信噪比下降时，特别是在1dB之后，有校正情况下的平均相关系数与次最大相关系数之差明显大于无校正的情况，这进一步说明本文提出的算法具有极强的低信噪比适应性。

仿真3 多项式码重对相关系数的影响

由式（19），式（32）以及式（34）可知，多项式中1的个数决定了反正切运算中，乘积因子的个数，这里将多项式系数1的个数定义为多项式码重，由此多项式码重值决定了ηvk，t，η′vk，t，η″vk，t的值，而这3个变量在估计各路信息序列时，至关重要，所以有必要研究多项式码重对于相关系数的影响。验证时，设定交织长度为1 000，截获码块数目为2 000，选定分量编码器为（21，23），（23，25），（23，35）以及（23，37），4种 RSC码，对应于多项式码重分别为5，6，7，8.记录在不同码重下，有校正与无校正条件下，正确交织位置的相关系数以及次最大相关系数值，结果如图4所示。

从图4结果来看，多项式系数对于相关系数具有一定的影响，从图4（a）来看，在高信噪比条件下，多项式码重对于有校正情况影响较小，在信噪比较低时，码重的影响才比较明显的表现出来，而对于无校正的情况，无论是高信噪比还是低信噪比条件下，影响都比较明显；从图4（b）来看，码重的影响规律与图4（a）基本一致，说明有校正的算法对于多项式码重的鲁棒性要强于无校正的算法。

图4 多项式码重对相关系数影响Fig.4 Influence of polynomial weights on correlation coefficients

3.2 算法容错性验证

本节进一步考察，提出的算法在有噪声环境下的适应能力。考察从3个方面进行，首先考察在不同交织长度下，算法的识别性能变换情况；其次考察当交织长度一定时，截获帧块数目对算法性能的影响；最后考察多项式系数码重对于算法性能的影响。为了突出在有校正情况下算法的优势，本节将在同一条件下，将2种情况放在一起进行对比。

仿真1 交织长度对算法性能的影响

设定交织长度L分别为64，128，256，512和1 024，交织类型为随机交织方式，设定截获数据帧数目为1 000，设定噪声变化范围为－4.5到0dB间隔0.125dB取值，分别采用有校正和无校正条件下对交织器进行识别，蒙特卡罗实验次数为1 000次，只有当全部交织关系都完成了识别，才能算一次正确的识别，记录在不同信噪比下有校正与无校正条件下交织器的正确识别概率，结果如图5所示。

从图5结果来看，随着交织长度的增加，算法性能逐渐变差，同时交织长度越大，算法性能变差的速度越快，但是总体来看，算法在低信噪比下的适应能力较好，如在交织长度为1 024，信噪比为－2dB条件下，识别率能够达到100%。同时与无校正情况对比来看，算法性能提高了近0.75dB。

仿真2 截获帧数对算法性能影响

图5 交织长度对算法性能的影响Fig.5 Influence of interleaver length on algorithm performance

仿真设定交织长度为512，交织方式为随机交织，设定截获的码块数目N分别为500，1 000，1 500，2 000，2 500，设定信噪比变化范围为：－5.5到－0.5dB，间隔0.125dB取值，蒙特卡罗试验次数为1 000次，同样在有校正以及无校正两种情况下，统计参数的识别概率，结果如图6所示。

从图6结果来看，当截获帧块数目增大时，算法的识别性能得到了有效的提升，主要原因在于截获的数据帧块越多，序列之间的相关性就越接近真实的情况，交织位置就越容易正确识别，但是当截获的帧数增加时，算法的性能虽然能够得到明显的提升，但是算法的计算复杂度也会增加；同样与无校正的情况对比，可知有校正的算法性能明显好于无校正算法，性能提升接近1dB。仿真3 多项式码重对于算法性能影响

图6 截获帧块数目对算法的影响Fig.6 Influence of intercepted blocks on algorithm

由3.1中，仿真3可知，多项式码重对于算法的性能具有较大的影响，在本节中，进一步研究多项式码重对于算法容错性能的影响。设定交织长度为256，交织方式为随机交织，截获数据帧数为1 000，选定分量编码器多项式为：（21，23），（23，25），（23，35），（23，37）以及（37，33），5种 RSC码，分别对应码重w 为5，6，7，8，9。蒙特卡罗次数为1 000，同样在有校正和无校正两种情况下，记录参数的识别概率，结果如图7所示。

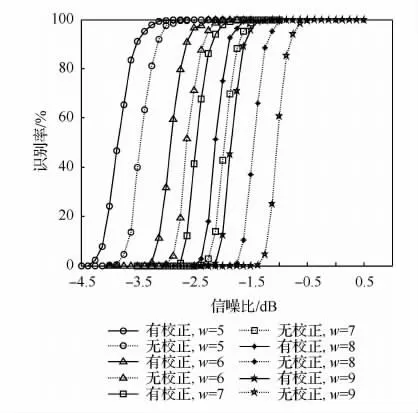
图7 多项式码重对算法性能的影响Fig.7 Influence of polynomial weights on algorithm

从图7来看，码重对于算法性能的影响比较明显，码重越小，算法的识别率越高；从识别率来看，相比较于无校正情况，存在校正的算法性能平均提高了近0.5dB，并且随着码重增加，提升越明显；从对码重的鲁棒性来看，有校正算法分别在w＝5，w＝9两种情况下识别率刚好降低到0时的信噪比为－4.375和－2.375dB，二者相差2dB，对于无校正算法，识别率刚好降低到0时的信噪比分别为－4.125和－1.5dB，二者相差2.625dB，说明有校正的算法的鲁棒性要好于无校正的情况。

3.3 与其他算法比较

本节将现有的算法与本文算法进行对比。本节选取的算法是基于校验符合度下的识别算法［17］以及文献［19］基于Gibss改进的识别算法；对比时，设定交织长度为64和512两种情况，截获的帧块数目为300，将本文算法（有校正与无校正两种方式）与之相对比，结果如图8所示。

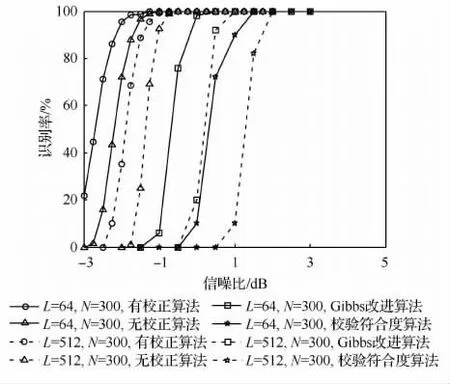
图8 不同算法性能对比Fig.8 Comparison of performances of different algorithms

从图8的结果来看，本文提出的识别算法要明显好于文献［17，19］中的算法，有校正的算法性能相比较于Gibbs算法，性能提升了接近2dB，而对比于校验符合度算法，其性能提高了接近3 dB。分析主要的原因在于，本文所提出的算法是将估计的序列与原始每帧遍历位置上的序列作相关运算，这种相关运算更能从整体上反映两个序列之间的相似程度，同时算法还可以利用估计的序列对原始序列进行校正，从而克服了以往算法性能随着交织长度的增加而急剧恶化的缺点。

其次，进一步对比算法完成一次可靠识别，所需要的最小数据量。设定交织长度L分别为64，128和512，信噪比设定为0和1dB两种情况，分别记录完成一次可靠识别，4种算法所需要的最少数据帧数目，记录结果如表1所示。

从表1中，4种算法完成一次可靠识别所需要的数据帧量来看，本文所提出的算法所需要的数据量最小，大约为文献［17］算法所需数据量的1／10以及文献［19］数据量的1／4。从2.3节中计算复杂度分析可知，在交织长度以及帧块数目相同的条件下，本文算法与文献［17，19］的算法计算复杂度相当，从完成一次可靠识别所需要的数据帧数来看，本文算法所需要的帧数要远远小于文献［17，19］中算法，由此从完成一次可靠识别的计算复杂度出发，本文算法的实时性最好。

表1 4种算法完成一次可靠识别所需要帧数目对比Table 1 Comparison of the data required for a reliable identification among 4algorithms

综合算法的容错性能以及实时性能两个方面，本文所提出的算法要好于现有的算法。

4 结 论

1）从Turbo码编码结构出发，提出了具有较强低信噪比适应能力的随机交织器识别算法，该算法首先利用截获的每路软判决信息实现交织位置信息序列预估计，然后将预估计的序列与原始序列作相关运算，相关性最大的位置即为交织位置；仿真实验证明了算法的能够实现序列的正确估计，同时能够实现低信噪比下交织关系的正确识别。

2）通过仿真，详细分析了多项式码重对最大相关系数以及次最大相关系数的影响，当多项式码重增加时，序列的最大以及次最大互相关性都会减弱；同时在有校正情况下，最大与次最大相关性之间的差异明显大于无校正情况，这说明了有校正的算法对于多项式码重的鲁棒性要强于无校正的算法。

3）考察了算法的容错性能，研究了交织长度、截获数据帧量、多项式码重因素对算法性能的影响，从结果来看，交织长度越大，算法的识别率将会降低，但是通过增加截获的数据帧量，可以改善交织长度较大所带来的缺点，同时多项式码重的增加会使得估计的序列与原始序列的相关性减弱，从而造成算法的性能变差，同样可以增加数据帧数，解决这一问题。

4）在容错性能以及所需要的数据量上，与现有的算法进行了对比，从结果来看，本文的性能提升了2～3dB，同时完成一次可靠识别所需的数据量减少了近原数据量的1／4。