LFM-BPSK复合调制参数快速估计及码元恢复
李 娟,戴曜泽
(1. 南京科瑞达电子装备有限责任公司,南京211100; 2.中国航天科工集团8511研究所,南京210007)
0 引 言
随着电子技术的发展,LFM-BPSK复合调制波形具有良好的抗干扰、低截获、多普勒不敏感等优点,在脉冲压缩雷达中得到越来越广泛的应用。因此,如何在复杂的电磁环境中有效、快速地侦察、分析及估计出此类复杂雷达调制信号以实现对新体制雷达进行准确迅速截获具有很强的作战应用意义。
目前,国内外已有不少文献提出了各种参数估计的方法。文献[1-2]提出小波变换、相位拟合、相位谱商特性等参数估计算法,但计算量大。最大似然法[3]、基于循环谱最小均方误差法[4]、基于二阶统计量最大似然法[5]等计算量小,但这些方法多是基于合作接收机或已知部分先验知识的前提。在电子侦察中,由于没有任何先验知识,这些方法的性能都会下降甚至失效。Gardner等提出了基于循环谱的幅度特征的相位编码信号盲估计参数估计方法[6],但由于计算量大、数据储存空间大等缺点,不适宜电子侦察的实时处理。文献[7-9]提出了基于Wigner时频分布的侦察信号参数估计方法,但需要在时频平面进行二维搜索,计算量也较大。
本文基于信号的平方、短时积分及短时傅里叶变换运算对LFM的调频斜率、初始频率及BPSK的码元速率进行了快速参数估计,其计算量和存储空间需求较小,可在硬件中实时实现。
1 信号模型
LFM-BPSK复合信号的相位为
(1)
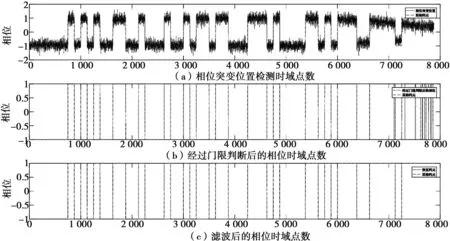
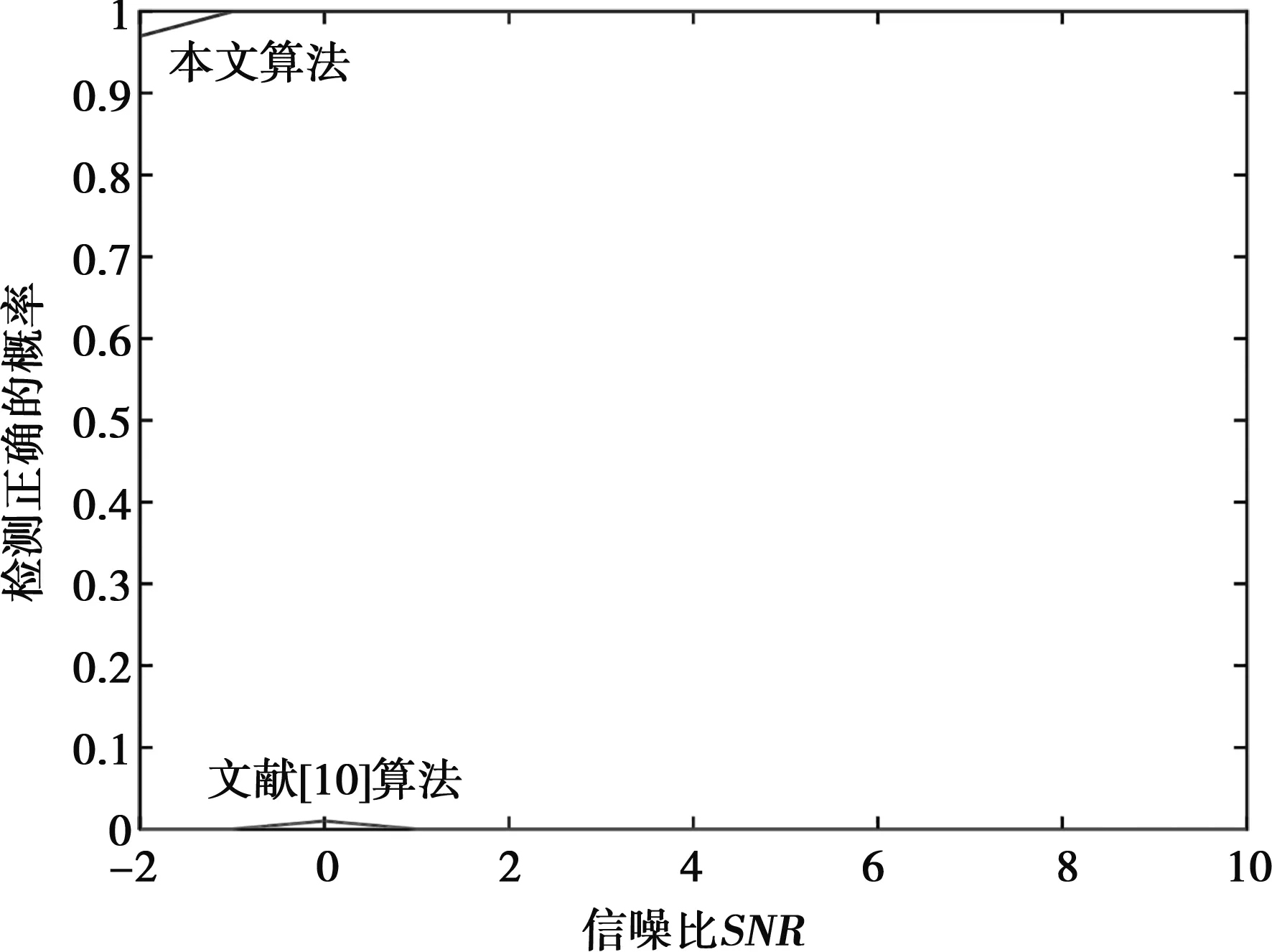
式中,k为调频斜率,f0为初始频率,Tb为码元宽度,N为码元个数,∏为持续时间为Tb的矩形窗,当且仅当0≤t 由式(1)可得LFM-BPSK复合信号的表达式如下: (2) 式中,φ0为信号的初始相位,Tb为码元宽度,NTP为脉冲的持续时间。 LFM-BPSK信号的时频曲线兼具了LFM与BPSK的特点,其时频曲线如图1所示。LFM-BPSK信号平方后的时频曲线仅剩LFM的特点,其时频曲线如图2所示。 图1 LFM-BPSK信号时频图 设侦察接收机接收的信号1如下: 图2 LFM-BPSK信号平方时频图 (3) 式中,w(t)为均值为0、方差为σ2的高斯白噪声。此仿真假设已提取出脉内信号,即信号的脉宽T=NTP已知,在此基础上估计LFM-BPSK信号的起始频率f0、调制斜率k、初始相位φ0、码元宽度TP并对码元进行恢复。 由图1可知,若实现LFM信号的起始频率f0和调制斜率k的估计,必须先消除BPSK的相位突变,然后利用快速解线性调频的算法解算出LFM信号的起始频率f0和调制斜率k。由图2可知,LFM-BPSK信号的平方可消除BPSK的相位突变,LFM的起始频率f0和调制斜率k经平方变为2f0和2k。其具体的解算过程如下: (1) 将式(3)平方得 x2(t)=[s(t)+w(t)]2 =s2(t)+2s(t)w(t)+w2(t) =ej(4πf0t+2πkt2+2φ0)+w2(t)+2w(t)× =slfm2+w′(t) (4) 式中 slfm2(t)=ej(4πf0t+2πkt2+2φ0) (5) (6) 因此,x2(t)可看成一个被噪声w′(t)污染的起始频率为2f0、调制斜率为2k的线性调频信号slfm2(t),要估计线性调频参数可用快速线性调频算法进行计算。 (2) 估计线性调频slfm2(t)斜率 =ej(4πf0t+2πkt2+2φ0)×e-j(4πf0(t-τ)+2πk(t-τ)2+2φ0) =ej(4πktτ+4πf0τ-2πkτ2) (7) (8) (3) 估计线性调频信号slfm2(t)起始频率 (9) (10) 由式(3)可知,平方运算消除了复合调制的相位突变,从而将复合信号参数估计问题转换为线性调频信号参数估计问题,避免了时频分析的二维搜索。但是,由式(4)可知,由于平方运算造成了信噪比的降低,因此算法无法适用信噪比过低的场合。信噪比低于-2 dB时,由于噪声的影响会造成信号检测错误,从而使参数估计失败。因此,在应用此算法前应用时域、频域滤波等方法提高信噪比。另外,信号平方后还可能导致f2频率模糊问题,因此在计算f2时要利用原复合信号频率所在的位置对f2进行解模糊。 由2.1节可重构线性调频信号为 (11) 根据式(4),原信号平方后与重构信号的平方共轭相乘为 =[ej(4πf0t+2πkt2+2φ0)+w2(t)+2w(t)× =ej(4πΔf0t+2πΔkt2+2φ0)+w2(t)+2w(t)× (12) (13) 因为w(t)为均值为0、方差为σ2的高斯白噪声,式(13)可简化为 (14) 通过2.2节可重构出带初相的线性调频信号为 (15) 原信号与重构信号的共轭相乘得 (16) 图4 相位编码码元速率 由图3、4及误差率可看出,信噪比为5 dB时可精确估计出复合信号的参数。可见,短时积分能够快速实现码速率的快速精确估计。但是,在选择积分长度T0时,要满足T0 (17) (1) 对BPSK_base信号取实部,其图如图5(a)所示。图中,“……”表示原始码元,“┅┅”表示含有噪声和误差的码元。 (2) 对含有噪声和误差的码元以0为门限进行1,-1判断,当码元大于或等于0时码元判断为1,否则码元为-1。经过门限判断后的图如图5(b)。图中,“……”表示原始码元,“┅┅”表示经过门限判断过后的码元。 (3) 由图5(b)可知,由于噪声和估算精度的影响,会造成码元存在毛刺,利用积分算法对码元进行去毛刺。去掉毛刺后的码元如图5(c)。图中,“……”表示原始码元,“┅┅”表示去掉毛刺后的码元,可看出去掉毛刺后的码元与原码元完全重合,在此基础上对码元进行恢复。 (4) 在利用计数恢复码元时,由于码元速率误差会使码元恢复过程中的误差个数随着码元个数的增加而增大。比如,第1个码元有1个采样点的误差,则第2码元则有2个采样点的误差,以此类推。当第100个码元时则会出现100个采样点的误差,从而可能无法正确恢复出码元。因此,在码元恢复过程中,要利用码元的突变对计数器进行清零,去除积累误差,然后找码元的中值点,利用中值点的数值对码元进行赋值。 图5 码元恢复过程 本文提出的LFM-BPSK复合信号参数快速估计及码元恢复算法以FFT运算为核心,辅以少量的乘法运算和正余弦运算,无矩阵相关运算。信号平方、延时共轭相乘及翻转共轭相乘主要是复数乘法可调用mul核实现,在计算调制斜率所需的两次FFT运算时可调用fft核实现。在调用fft核时,应考虑傅里叶变换的长度,采样率越高脉宽越宽,所需的傅里叶点数越多,从而使用的资源越多。在设计前期因考虑FPGA所能适应的最大采样率及最长脉宽,当超出资源时应适量减少傅里叶变换的长度,以测量精度换取资源。脉宽越长测频精度越高,采样率越高,能测量的瞬时带宽越大,但同样消耗的资源越多。计算信号的初始相位时可调用cordic核实现。信号恢复过程可用dds核或cordic核实现,码元恢复过程仅需要少量的LUT逻辑门便可实现。纵观LFM-BPSK复合信号参数快速估计及码元恢复算法其主要消耗DSP48E硬件资源,辅以少量的LUT逻辑门便可实现,是一种硬件可实现的参数快速估计及码元恢复算法。 为了验证本文算法的有效性,做了如下仿真: 仿真中,码元速率Cp=107,码元个数N=63,信噪比SNR=-2:10 dB,步进为1。在此条件下,利用本文算法与文献[10]算法分别做100次蒙特卡罗仿真,其码元恢复的正确率如图6所示。由图6可看出,本文算法在信噪比大于0 dB时码元的正确率为100%,可以完美恢复码元,但文献[10]所提供的算法无法正确恢复出码元。基于以上情况,在SNR=10 dB时,查看文献[10]的码元恢复情况。由图7可知,文献[10]算法前20个码元可以准确地恢复。但是,随着码元速率误差的积累,使后面的码元无法正确恢复。因此,文献[10]所提供的算法无法支撑长码恢复,而本文算法无此限制。 图6 不同算法码元恢复的正确率 图7 SNR=10 dB码元恢复 基于LFM-BPSK复合信号的特点,本文先利用平方运算将复合调制信号参数估计转换为单一线性调频参数估计,恢复线性调频信号,与原信号共轭相乘,恢复相位编码基带信号,对编码信号进行参数估计及码元恢复。通过第2节的理论分析及第3节的仿真,本文提出的算法可利用硬件快速实现并达到良好的码元恢复效果,是一种工程可实现算法。但是,此算法在参数估计中涉及了平方运算,造成信噪比降低,因此在利用此算法之前应用时域、频域滤波或其他积累算法提高信号的信噪比。
2 算法原理

2.1 LFM参数快速估计
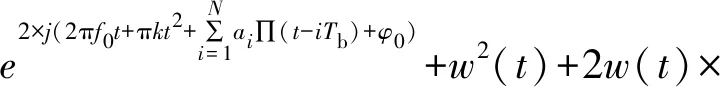
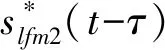


2.2 复合信号初始相位估计

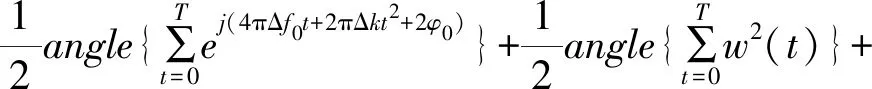

2.3 BPSK码元速率估计


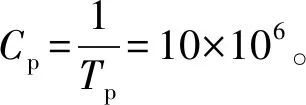

2.4 BPSK码元恢复
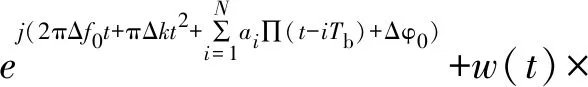
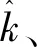
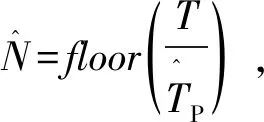
3 性能分析
3.1 硬件可实现分析
3.2 仿真结果

4 结束语

