基于极大似然准则的短猝发信号盲解调
闫红超,杨 松
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
基于极大似然准则的短猝发信号盲解调
闫红超,杨 松
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
针对非协作通信中短猝发信号准确接收的需求,在对短猝发信号进行建模的基础上,提出了一种基于极大似然准则的短猝发信号盲解调算法。根据极大似然准则,对前期信号参数估计得到的可能码元个数集合进行搜索处理,获取不同码元个数对应的第一个码元起始点位置,计算相应的重构信号与接收信号的似然度,据此实现短猝发信号码元个数的准确估计并恢复符号序列。应用二进制方波信号对盲解调算法进行仿真,仿真结果表明,当短猝发信号码元个数>8个,信噪比>10 dB时,码元个数估计正确率能够达到95%以上,解调效果良好。
短猝发;盲解调;码元估计;极大似然准则
0 引言
猝发通信是现代数字通信的一种重要通信手段,已经广泛应用于微波通信、卫星通信、移动通信、应急通信等共享媒介通信系统中[1]。猝发信号持续时间较短,因此对猝发信号的解调处理有更高的要求[2]。
目前没有对短猝发信号的明确定义,本文研究的短猝发信号特指持续时间很短,传输码元个数小于128个码元的猝发信号。协作通信中,通信双方利用已知信息提高信号解调质量,但在电子对抗等非协作条件下,接收信号特征参数未知,接收方需要对接收信号的载波频率、符号速率等参数进行估计[3]。短猝发信号码元个数较少,最少时只有几个码元,传统的信号分析算法只能给出可能的符号速率集合,无法精确得到短猝发信号的符号速率信息[4],给信号解调处理带来了困难。本文提出了一种基于极大似然准则的盲解调算法,能够实现短猝发信号的正确接收。
1 信号模型及参量估计准则
接收端得到的复基带短猝发信号表达式为[5]:
(1)
为了说明算法的思路且不失一般性,这里主要讨论二进制基带方波信号的接收处理。此时,式(1)可以表示为:
(2)
在不考虑残余载波频偏和相位时,短猝发信号经过整数倍采样后可以表示为:
sM,k+n(k),
(3)
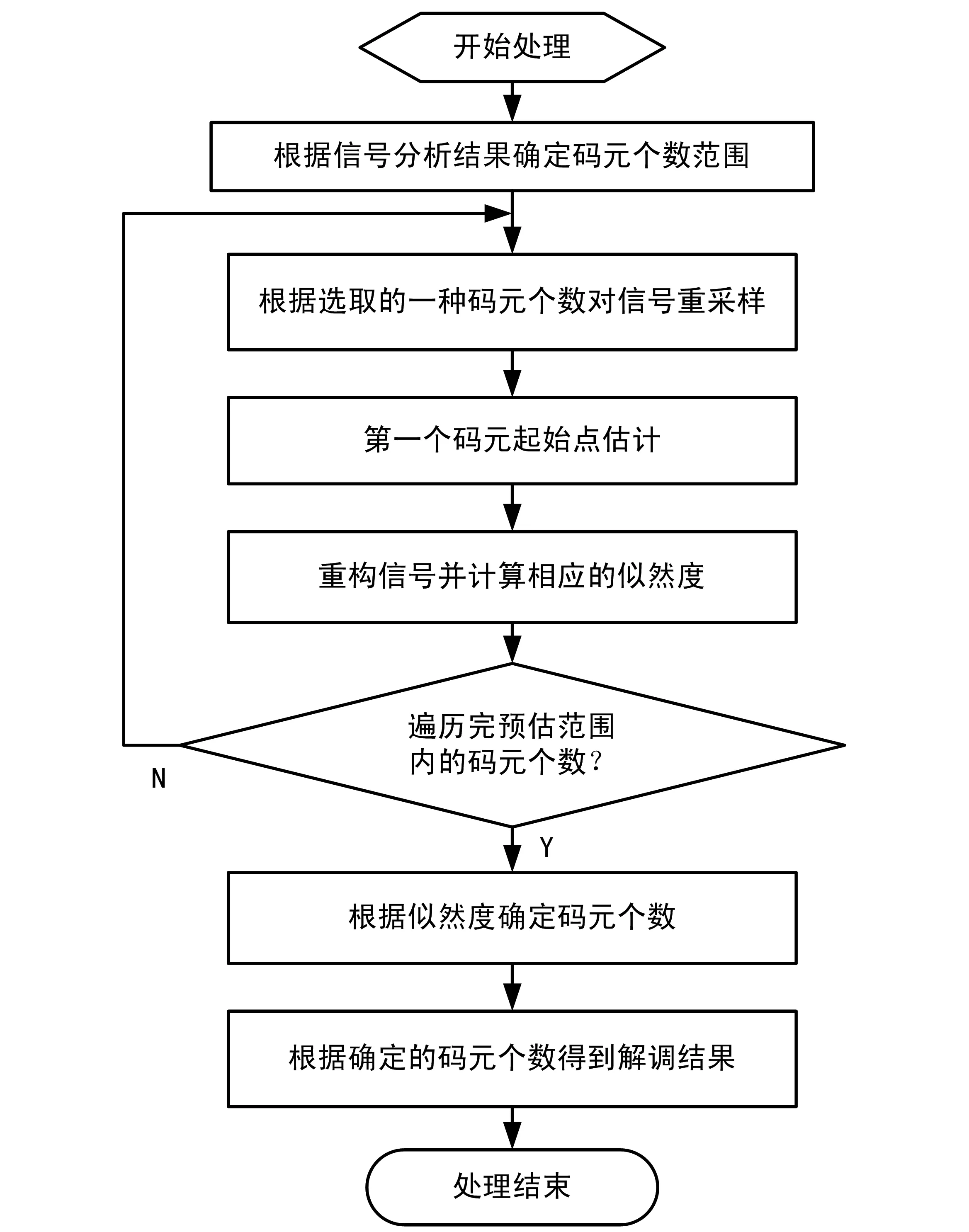
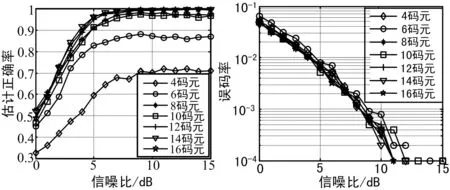
1≤k≤N;0≤n0 式中,N为总的采样点个数;N0表示每个码元包含的采样点个数,n0表示第一个码元前的采样点个数,表征信号的传输时延;i表示一个码元内的第几个采样点;{sm(k)}为双极性方波信号,取值为-1或1;sM,k为双极性方波信号的简化表示。对上述信号的盲解调就是对非随机的未知参量M、n0的联合盲估计,其中采样序列y(k)和采样点数N已知。 常用的参量估计准则有贝叶斯准则、最大后验概率准则和极大似然准则等[7]。对于非随机参量的估计,极大似然估计具有优越的渐进性能,成为通用的一种估计方法[8],因此本文采用极大似然准则对非随机的信号参量进行估计。 最大似然度对应的码元个数就是实际码元个数的极大似然估计值,获得码元个数的估计值后恢复得到相应的解调信息。 基于极大似然准则的短猝发信号盲解调算法处理流程如图1所示。 图1 基于极大似然准则的盲解调算法处理流程 算法关键技术有: ① 第1个码元起始点估计:在固定一种码元个数M的条件下,根据极大似然准则,估计第1个码元的起始采样点位置; 2.1 第一个码元起始点估计 接收信号码元格式如图2所示。 图2 接收信号码元格式示意图 对图2所示码元格式的信号进行盲解调,首先要确定第1个码元的起始采样点位置。接收信号无法保证每个码元内的采样点个数为整数,因此需要根据分析算法给出的符号速率信息对信号进行重采样[9],使得每个码元内的采样点个数为整数。设当前进行搜索处理的码元个数是M,重采样后的采样点个数为N2,过采样率为η。对n0进行遍历估计前首先对各采样点数据进行一次硬判决:小于0的认为是-1,否则认为是1,得到硬判决数据。 延时部分可能包含的采样点个数n0为0~η-1,因此可以在这个范围内对延时部分占用的采样点个数进行搜索估计。根据n0的不同取值,将硬判决数据划分为M+1块:第1个采样点到第n0个采样点是第1块(若n0=0则第1块为空);第n0+1个采样点到第N2个采样点按照过采样率η平均划分为M块。将硬判决数据分块后,统计各个块中误码个数的估计值:在各个块中,统计-1和1的个数,较少的个数认为是该块数据的误码个数enm。将各个块中的误码个数相加,得到当前认为的延时部分包含的采样点个数n0对应的总误码个数 : (4) 对延时部分包含的采样点个数在0~η-1范围内进行搜索,得到相应的误码个数。误码个数最少时对应的采样点数n0就是延时部分包含的采样点数的极大似然估计值,第1个码元从第n0+1个采样点开始。 2.2 似然度的计算 对于一种给定的码元个数M,获取第1个码元的起始点位置n0+1后恢复信号并计算似然度。 恢复信号与接收信号之间的似然度,可以利用欧氏距离进行度量。对于高斯白噪声中的信号,基于极大似然准则的判决规则就简化为寻找在距离上最接近于接收信号向量的恢复信号,该判决规则叫做最小距离检测[10]。与接收信号的欧氏距离最小的恢复信号对应的码元个数,就是实际码元个数的极大似然估计值。 (5) (6) 欧氏距离最小时对应最大的似然度,似然度最大对应似然函数达到最大[12]。通过对码元个数M及延时部分包含的采样点个数n0的二维搜索,找到最大似然度对应的码元个数,就是实际码元个数的极大似然估计值,此码元个数对应的解调数据即为解调结果。 用MATLAB产生的仿真信号对算法进行测试:根据设定的码元个数随机产生0、1码流;信号过采样率随机产生,设置为4~20之间;产生信号后,对信号的起始部分随机去掉几个采样点,使接收信号符合图2所示的形式。 仿真条件:码元个数依次设置为4、6、8、10、12、14、16;信噪比范围设置为0 ~15dB;针对不同的码元个数分别进行10 000次蒙特卡罗仿真,将仿真结果进行对比,分析算法的性能。 码元个数估计正确率结果对比如图3所示。从图3的结果可以看出,随着信噪比的增加,码元个数估计正确率呈现上升趋势,在 10dB时达到收敛。4码元、6码元、8码元、10码元、12码元、14码元、16码元情况下,估计结果收敛时对应的估计正确率分别为70.3%、87.4%、95.3%、96.8%、98.4%、99.5%、99.7%。码元个数越多,估计正确率越高,当码元个数>8个,信噪比>10dB时,码元个数估计正确率达到95%以上。 在正确估计码元个数的基础上,不同码元个数对应的解调误码率对比如图4所示。从图4的结果可以看出,随着信噪比的增加,信号解调误码率呈现下降趋势,在信噪比为12dB时误码率基本达到1×10-4,不同的码元个数在相同信噪比时误码率性能相差不大,能够满足短猝发信号盲解调的需求。 图3 码元个数估计结果对比图 图4 不同码元个数解调误码率对比图 当码元个数较少时,随机产生的0、1码中连0或连1的概率增大,造成码元个数估计正确率降低。当码元个数为4时,随机产生的0、1码序列可能出现0011、1100、0000、1111等序列,此时将无法正确估计码元个数。 本文提出了一种基于极大似然准则的短猝发信号盲解调算法,对算法关键技术进行了详细阐述。新算法解决了非合作接收条件下短猝发信号符号速率分析不准确的问题,通过码元个数搜索实现了短猝发信号的符号速率估计与信号解调。仿真结果验证了算法的正确性与可行性,具有实际应用价值。 [1] 崔诵祺,安建平,王爱华,等.低信噪比、高动态环境突发信号检测与估计[J].北京理工大学学报,2013,35(3):304-309. [2] 杨晗竹,李广侠,赵陆文,等.突发信号前向频偏估计方法综述[J].无线电通信技术,2015,41(6):10-15,26. [3]HamidrezaHosseinzadeh,FarbodRazzazi,AfroozHaghbin.AnAdaptableArchitectureforBlindModulationsClassificationinVariableSNREnvironments[C]∥2012 6thIEEEInternationalConferenceonIntelligentSystems(IS),2012:164-169. [4] 廖 明.短时突发PSK信号分析和盲解调技术研究[D].北京:中国工程物理研究院,2014:1-17. [5]NikolicBZ,DimitrijevicBR,MilosevicND,etal.PerformanceofMPSKSignalPredetectionEGCdiversityreceiver[C]∥2012 20thTelecommunicAtionsForum(TELFOR),2012:460-463. [6] 许小东.非协作数字通信系统盲解调关键技术研究[D].北京:中国科学技术大学,2007:11-16. [7] 赵树杰.信号检测与估计理论[M].西安:西安电子科技大学出版社,1998. [8] 张明友,吕 明.信号检测与估计(第2版)[M].北京:电子工业出版社,2005. [9] 张丽娜,潘申富.数字重采样误差对解调性能的影响分析[J].无线电工程,2011,41(2):19-20,50. [10]琚瑛珏.恒包络调制解调技术研究与实现[D].长沙:国防科学技术大学,2011. [11]MouradBarkat.SignalDetectionandEstimation(SecondEdition)[M].Boston:ARTECHHOUSE,INC.2005. [12]陈 璐,仰枫帆.MSK信号的最大似然检测[J].无线电工程,2015,45(1):68-71. Blind Demodulation Algorithm for Short Burst Signals Based on Maximum Likelihood Rules YAN Hong-chao,YANG Song (The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China) Aiming at the demand for blind demodulation for short burst signals,a blind demodulation algorithm for short burst signals based on maximum likelihood rules is presented based on short burst signal modeling.According to the maximum likelihood rules,the possible number of symbol estimated from the preceding signal parameters are searched and processed to obtain the start point of the first symbol,and the relevant likelihood of reconstitution signals and receiving signals are calculated.The exact estimation of symbol number of short burst signals is realized and the symbol sequence is restored.The blind demodulation algorithm is simulated by using binary quare wave signals,and the results show that the the correctness of symbol number estimation can be more than 95% and the demodulation effect is better when the symbol number of short burst signal is more than 8 and the signal-noise ratio is more than 10 dB. short burst signals;blind demodulation;estimation of symbol number;maximum likelihood rule 10.3969/j.issn.1003-3114.2016.06.13 闫红超,杨 松.基于极大似然准则的短猝发信号盲解调[J].无线电通信技术,2016,42(6):52-55. 国家部委基金资助项目 2016-07-26 闫红超(1983—),男,工程师,主要研究方向:信号解调、数字信号处理。杨 松(1986—),男,工程师,主要研究方向:信号分析、信号解调。 TN911 A 1003-3114(2016)06-52-4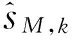
2 算法处理流程及关键技术
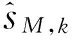


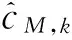

3 算法仿真
4 结束语

