一类可化为一阶线性微分方程的微分方程求解

常丽娜

(长治学院 数学系，山西 长治 046011)

0 引言

众所周知，对于一般的一阶常微分方程并没有通用的初等解法，比如形式上很简单的里卡蒂(Riccati)方程一般就没有初等解法，事实上大量的一阶非线性微分方程都无法用初等解法求出其通解，只能利用数值方法求出其数值解或近似解[1].本文给出了一类可通过变量变换化为一阶线性微分方程的微分方程，从而为此类微分方程提供了一般的求解方法.

1 主要方法及举例

设有微分方程形如

(1)

其中P(x),Q(x)在考虑的区间上是x的连续函数，其中当Q(x)=0时，方程为变量分离方程，故本文中主要讨论Q(x)≠0的情形.

方法1：化为伯努利微分方程

分析：方程形式上和一阶非齐次线性微分方程最为接近，故令z=ey，希望使得方程右边可化为线性形式.

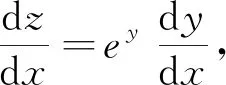
(2)

方程(2)为n=2的伯努利微分方程.伯努利微分方程可利用积分因子法、常数变易法来求得通解或通过变量代换令u=z-1化为一阶非齐次线性微分方程来求得其通解.

启发：方程形式上和一阶非齐次线性微分方程的区别在于一阶非齐次线性微分方程右边为P(x)y+Q(x)，上面令z=ey，两边求导的过程中，因为指数函数ey求导仍含其本身，所以并没有将P(x)ey化为P(x)z，而是将P(x)ey化为P(x)y2，并未达到我们将方程(1)直接化为线性微分方程的目的.实际上，再次观察(1)的形式及指数函数ey的求导特点，令z=e-y，两边求导后，将变换代入方程，可将P(x)ey的部分化为-P(x)，Q(x)化为-Q(x)z，即此时方程右边已化为线性形式.

方法2：直接化为一阶非齐次线性微分方程

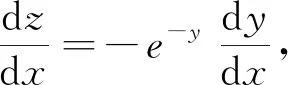
(3)

此为一阶非齐次线性微分方程，我们可利用常数变易法、积分因子法等初等方法求得其通解.

因为伯努利微分方程一般也是通过变量变换化为一阶非线性微分方程来求解的，所以比较两种变换，易知方法二更简便.

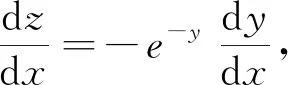
(4)

这是一阶非齐次线性微分方程，首先，对应齐次线性微分方程

的通解为

z=cx-3

其次应用常数变易法，将上式中的c看成为x的待定函数c(x)，设出非齐次线性微分方程的通解，即

z=c(x)x-3.

(5)

将上式代入(4)，得到

即

积分之，求得

将所求的c(x)代入(5)，得方程(4)的通解

代回原来的变量y，得到原方程的通解

其中c′为任意常数.

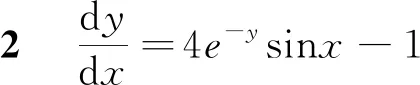
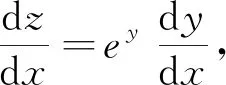
这是一阶非齐次线性微分方程，解得

代回原来的变量y，得到原方程的通解

ey=ce-x+2ex(sinx-cosx)

其中c为任意常数.

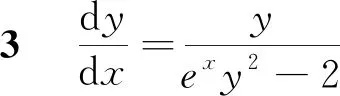
解：原方程不是未知函数y的可化为线性微分方程的这类方程，但我们可将它改写为

即

把x看作未知函数，y看作自变量，这样方程就是可化为线性微分方程的这类方程.

这是一阶非齐次线性微分方程，解得

z=cy2-y2ln|y|

代回原来的变量x，得到原方程的通解

e-x=y2ln|y|-cy2

其中c为任意常数.

微分方程的求解灵活性非常强，对于非常见类型可根据方程的特点，引进适当的变量变换，将方程化为常见类型后进而求解，本文根据一类典型类型的微分方程特点，进行适当的变换，将一类非线性微分方程化为线性微分方程求解，从而为一阶微分方程的初等解法进行了一定的推广.