关于伯努利方程的解法探讨
2018-09-07 06:34:36张玮玮陈定元
安庆师范大学学报(自然科学版) 2018年3期
张玮玮,陈定元
(安庆师范大学数学与计算科学学院,安徽安庆246133)
伯努利方程是常微分方程中的一类重要方程,在工程、物理学中有着广泛的应用。伯努利方程是一类特殊的一阶非线性常微分方程,对于其通解的研究在实际中有着重要的价值,常见解法是通过变量变换将其转化为一阶线性微分方程来进行求解[1-4]。本文将根据伯努利方程的结构特点,引入一种新的求解方法,最后通过具体例题说明方法的正确性和有效性。
形如

的方程,称为伯努利方程,其中P(x),Q(x)为x的连续函数,n≠0,1,是常数。
对于y≠ 0,方程两边同乘y-1,得到

两边积分得到:

猜想方程的解具有(2)式形式,将其带入方程(1),得到


即
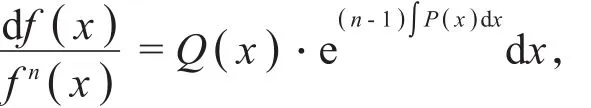
两边积分得到

其中C为任意常数。从而

所以原方程的通解可以表示为

其中C为任意常数。
下面通过例子来说明本文所得结果的正确性和有效性。
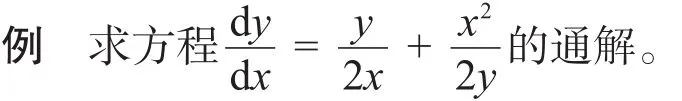

猜你喜欢
数学杂志(2023年1期)2023-03-17 00:22:58
河北大学学报(自然科学版)(2022年6期)2022-12-22 05:54:58
成都信息工程大学学报(2019年2期)2019-08-28 10:00:44
科技创新与应用(2017年3期)2017-02-18 17:43:44
发明与创新(2016年5期)2016-08-21 13:42:46
课程教育研究·学法教法研究(2016年7期)2016-04-26 16:03:25
新校园(下)(2015年6期)2015-07-04 05:06:49
广西科技大学学报(2015年4期)2015-02-27 12:22:25
金陵科技学院学报(2014年1期)2014-03-15 03:29:00
物理与工程(2014年4期)2014-02-27 11:23:09

