秩与维数教学中突出单位向量组的设计

赵正俊，孙广人

（安庆师范大学数学与计算科学学院，安徽安庆246133）

向量组的秩(或者矩阵的秩)与线性空间的维数是线性代数及高等代数中两个基本的概念，它们在线性方程组的求解、矩阵理论与线性空间理论中具有重要的地位。同时，这两个概念又具有一定程度的抽象性，是线性代数及高等代数教学与学习的难点，因此秩与维数的教学方法成为众多线性代数任课教师关注的焦点[1-6]。然而，从两个概念的内在关系出发统一处理相关知识点的教学设计在线性代数及高等代数相关教材文献中[7-9]相对少见。在实际教学中，作者曾尝试基于Gauss消元法提出在线性代数教学中突出行最简形的教学设计，该方法统一处理线性代数中行列式、矩阵以及线性方程组，获得了不错的效果。秩与维数的求解属于行最简形的应用——要选择能让学生留下深刻印象且更加具体的对象来促进教学，由作者多年的教学经验来看，单位向量组（或者单位阵）无疑是一个合适的选择。

1 向量组的秩

给定一个向量组确定它的秩并且求出一个极大无关组是线性代数教学中的难点。与确定矩阵的秩相比，学生对于求解向量组的秩显得更加困难。在教学过程中了解到很多学生开始学习时无法接受把向量组当成一个整体，进一步作成一个矩阵的想法，而众所周知这一做法是计算向量组的秩的关键。除此之外，不少学生也不理解行向量组为什么要通过转置再进行初等行变换来确定其极大无关组，更加不能想象通过这种方法来确定同一向量组中其余向量在极大无关组下的线性表示。实际教学中，作者适当突出了单位向量组的地位，帮助学生掌握这些比较难以理解的概念。

1.1 确定向量组的秩

如果一个向量组的极大无关组由单位向量组成，那么学生容易理解通过初等变换消去其余向量确定向量组的秩的做法。

例1三个行向量

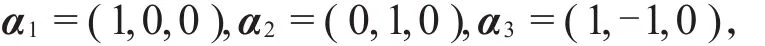
由于前两个是单位向量，α3是前两个向量的线性组合，学生能够理解作下列初等行变换可以确定这一向量组的秩：

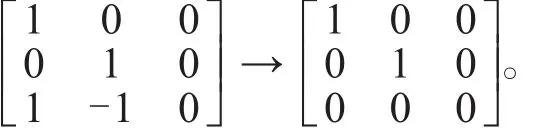
而对于相对复杂的向量组

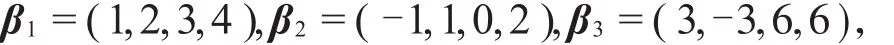
不少学生虽然知道向量组等价的概念，却不明白把向量组作成一个矩阵，然后对之实施初等行变换的做法。教师如果注意强调行最简形中的“单位向量组”，则有助于学生对于这一过程的理解。

关于行最简形的定义，可以参考通行的线性代数教材[3,7-9]。满足以下两个条件的矩阵A是行阶梯形：

（1）A的所有元等于0的行出现在所有非零行的下方；

（2）如果A的第1,…,r行是非零行，每个非零行的第一个非零元所在的列是j1,…,jr，则j1＜… ＜ jr。

进一步如果行阶梯形还满足以下条件则被称为行最简形：

（3）A的非零行的第一个非零元等于1，且它所在的列中只有1一个非零元。

例2以向量组

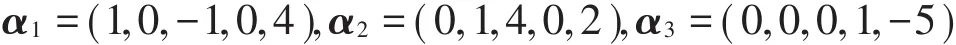
说明为什么需要行最简形，主要原因是这3个向量作成矩阵后其中1、2、4列会出现“单位向量组”：

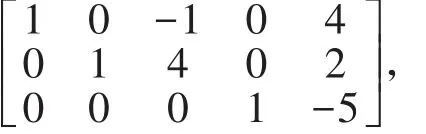
而之所以容易判断它们线性无关，是由于k1α1+k2α2+k3α3=0，当且仅当等式左侧线性组合中第1、2、4分量等于零。

至此，多数学生已明白确定向量组秩的方法：通过初等行变换消去“多余的向量”，而一种确定是否还有“多余的”向量的方法，即为检查“剩余”向量所组成的向量组的列中有没有与剩余向量个数相等的单位向量组。若需出现单位向量组，直接的方法是对向量组作成的矩阵实施初等行变换求其最简形，因此，某种意义上求行最简形即为通过初等行变换化简矩阵，使之出现单位向量组或者单位矩阵的过程。当然，求行最简形和化行阶梯形相比一般要做更多的初等变换，因此需向学生强调，如果只要求确定向量组的秩，则只需要把向量组构成的矩阵化成行阶梯形这种“不彻底”的形式即可。

1.2 初等行变换对列的影响

众所周知，之所以把一个行向量组作成的矩阵转置后再实施初等行变换来确定它的极大无关组，是由于初等行变换不改变矩阵的列向量之间的线性关系。具体地说，初等行变换使得线性相关的列依旧线性相关，线性无关的列依旧线性无关。然而对初学者来说，理论容易灌输，理解比较困难。因此选择一些典型的例子来说明这一原理，当然单位向量组又能起到很好的辅助作用。

例3在确定以下向量组

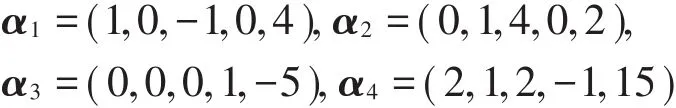
的一个极大无关组的过程中，典型做法是把它们作成一个矩阵并转置

根据例2，易看出前3个列的1、2、4行形成一个单位向量组，所以线性无关，而通过初等行变换化为行最简形

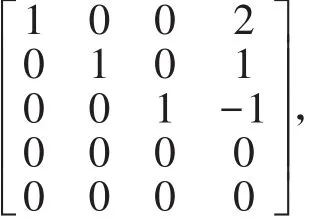
因此看出前3列依旧线性无关。此时可提示学生原向量组有如下关系：

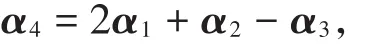
而上述矩阵最后一列前3个分量是2,1,-1，恰好是等式右侧3个向量的系数。

这样的神奇对应引起学生的兴趣，就可以引导他们分析深层原因。最终学生发现：之所以系数有这样精确对应，是因为研究一组行向量α1,…,αn的线性关系等价于研究齐次线性方程组

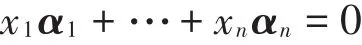
的解，该方程组的系数矩阵恰好是α1,…,αn做成矩阵的转置。而一旦其中某些向量线性无关，比如α1,…,αr它们转置后实施初等行变换变为行最简形，则αT1,…,αTr变化后所在列的前r行必然形成一个单位向量组。若α1,…,αr恰好是极大无关组，要考虑某个向量αi在极大无关组下的表示，相当于求解方程组x1α1+ …+xnαn= αi，而求解线性方程组相当于把增广矩阵(αT1,…,αTr,αTi)化为行最简形，即前r行前r列出现单位向量组的过程。

2 线性空间的维数

2.1 求线性空间的一组基

在考虑线性空间的一组基时，因单位向量组

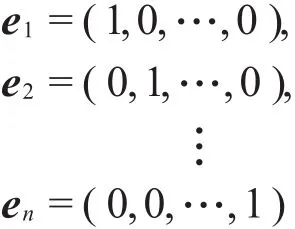
的线性无关性很显然，并且任意向量可以表示为

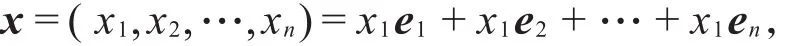
由此学生容易理解实数域上的线性空间V={x=(x1,x2,…,xn)|xi∈ R}维数是 n。然而学生对于求解给定一组向量α1,…,αn张成的线性空 间 W={x1α1+ … +xnαn|x1,…,xn∈ R}的 维数，是有一定难度的。教师通过与学生互动发现：产生这一困难的主要原因是学生并没有理解线性空间W的结构。事实上，W是由向量组α1,…,αn生成的子空间，而把α1,…,αn作成矩阵再作初等行变换后所得的行向量,…,等价于α1,…,αn，因此，W={x1+ …+xn|x1,…,xn∈ R}，这样，就可以把寻找W一组基与确定向量组的秩的过程等同。

例4选择例3中4个向量生成的线性空间W，如果需要确定W的一组基，进而确定W的维数，只需把它们作成矩阵并实施初等行变换

则前3行中1、2、4列即为3维单位向量组，因此前3行形成W的一组基。

如果要求在α1,…,αn中求W的一组基，这一过程与求解α1,…,αn的一个极大无关组的过程完全一致，因此可以模仿例3用单位向量组解释这一过程。

2.2 确定基础解系

关于基的另一个学习难点是基础解系，它是解空间的一组基，但是线性方程组的解的结构理论通常出现在线性空间之前，所以学生理解起来比较困难。在这里典型的做法是结合自由未知数，突出使用单位向量组来弥补概念的不足。

通过初等行变换把系数矩阵变成行最简形

因此有

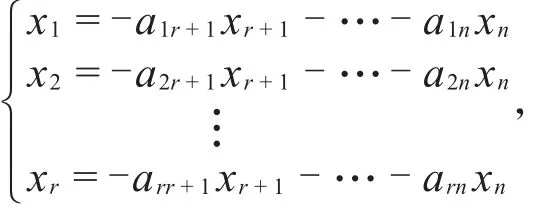
这样对自由未知数组(xr+1,…,xn)取遍n-r维单位向量组即得n-r个解向量，而由于n-r个解向量的最后n-r个列形成单位向量组，所以它们线性无关，并且任意解向量都是它们的线性组合。

解空间的概念发展到线性映射中变身为线性映射的核，而系数矩阵的行向量组张成的线性空间则对应系数矩阵的相伴线性变换的像。因此在研究线性映射的核与像时完全可以采取确定基础解系中选择单位向量组的方法。

3 总结

总的来说，单位向量组结构简单、地位重要且容易被学生记忆，以其为范本可以促进学生对秩与维数相关知识点的消化吸收。单位向量组是作者对以Gauss消去法为基础的行最简形的教学设计中频繁使用的范例，当然，作者的具体教学过程设计尚处于不太成熟的阶段，存在不合理的地方。例如，在确定向量组的秩的时候，仅需要求出矩阵的行阶梯形即可，再求行最简形已不必要。因此教师需要细致地编排教学内容，一方面使学生通过单位向量组能够快速理解矩阵的秩，另一方面，又能使大多数学生不会产生误解，以至于每次求矩阵的秩都去求矩阵的行最简形。另外，应该注意到，使用单位向量组来解释通过转置的方法求极大无关组的实际效果固然不错，额外的代价是需要耗费更多教学时间。因此，这一教学设计需要进一步加强相关知识点之间的融合以提高教学效率。