时变光子晶体及计算方法
方云团,李小雪,吴义恒
(1.江苏大学计算机科学与通信工程学院,江苏镇江212013;2.安庆师范大学物理与电气工程学院,安徽安庆246133)
电磁波在时间和空间的变化经过傅里叶变换分别由频率和波矢来描述,通过改变它们的对称性可以设计人工电磁材料来控制电磁波的传播,最常见的是光子晶体。通过打破材料连续空间平移对称变为离散空间平移对称(周期结构)就会改变频率和波矢的关系,形成所谓的光子晶体频率带隙结构。光子晶体自1987年由S.John和E.Yablonovitch分别独立提出以来[1-2],在材料科学、物理、光学、通信等领域引起广泛的兴趣[3-7]。研究光子晶体的理论依据是麦克斯韦方程组和固体物理的布洛赫原理。长期以来人们对光子晶体的研究局限在折射率空间周期变化的结构。但麦克斯韦方程组具有内在的时空对称性,除了打破材料连续空间平移对称变为离散空间平移对称,我们还可以打破材料连续时间平移对称变为离散时间平移对称,即材料折射率随时间周期变化,同样会改变频率和波矢的关系,形成另一种光子晶体带隙结构,这样会产生另一种形式的光子晶体。为区别起见,我们把折射率空间周期变化的光子晶体称“空变光子晶体”,而把折射率随时间周期变化的光子晶体称“时变光子晶体”。材料折射率随时间有规律变化在现实中也是可以实现的,像电光材料、压电材料、石墨烯材料[8]在时变电压控制下均能产生折射率时变的结果。虽然麦克斯韦方程组是时空对称的,但人们对光子晶体的研究明显处于不对称状态,几乎局限在空变光子晶体。在文献[9-10]中作者对时变光子晶体进行了研究,但作者使用的是平面波展开法,涉及复杂的数学运算。因为时变总是一维的,在折射率随时间跃变的情况下,可以使用更简明的传输矩阵方法来推导时变光子晶体的传输特性和色散关系。
1 理论推导
假设电磁波沿z轴传播,电场沿x轴,表示为Ex;磁场沿y轴,表示为Hy,它们都只是坐标z的函数。在电磁波的传播过程中,波数k决定相位随空间的变化,角频率ω决定相位随时间的变化,它们分别决定相位变化的空间频率(或周期)和时间频率(或周期)。在空变光子晶体的研究中,我们只考虑时谐场,即不考虑时间相位对传播的影响,只考虑空间相位对传播的影响,角频率ω不变,波数k是空间位置z的函数。在本文时变光子晶体的研究中,由于折射率不随空间变化,只随时间变化,我们只研究特定位置z处电磁波随时间的变化规律。在特定位置先假设波数k保持不变,不考虑空间相位对传播的影响,只考虑时间相位对传播的影响。此时角频率ω是时间t的函数。电磁波的形式为
把(1)、(2)式代入麦克斯韦方程得

将(3)式代入(4)式得


假设

其中,j=0,1,2,…。
(7)式表明折射率在一个时间周期单元T分成T1和T2两个时间段,时间周期晶格位于t0至NT,入射前(t<t0)和入射后(t>NT)背景折射率均为n0。折射率随时间的分布如图1所示。T1和T2对应空变光子晶体周期单元两层介质的厚度。借用空变光子晶体的分析方法,由于每个时间段折射率是常数,角频率ω也是常数。在T1时间段,ω1(t)=kc/n1,方程(6)的解为

(8)式右边类似于空变光子晶体两个相反方向平面波的叠加,角频率对应空间波数,时间t对应空间位移。(8)式右边第一项角频率为正,对应波的相位随时间增加;第二项角频率为负,对应波的相位随时间减少。产生负频率电磁波的原因是折射率的跃变产生反射。同样在T2时间段,ω2(t)=kc/n2,方程(6)的解为


图1 时变光子晶体的结构模型
由(4)式可分别求出T1和T2时间段的磁场

现在考虑电磁场在两个时间段的过渡。由(8)式可以看出,E1x(t)是时间t的单值连续函数,故在两个时间段分界处(表示为T1-2),有


(12)式和(13)式写成矩阵形式即为

电磁场在其他时间段分界处也有着同样的矩阵关系。
在T1和T2时间段内,根据(8)式,电场只有时间相位的变化,可用相位矩阵表示:


类似于空变光子晶体在出射空间没有反射波,在出射时间由于折射率不变,E-Nx=0,由此得到时变光子晶体的透射系数和反射系数:

类似于空变光子晶体透射系数和反射系数是角频率的函数,形成时间频率谱,时变光子晶体透射系数和反射系数将是空间波数k的函数,形成空间频率谱,从而体现了时空的对称转换。
空变光子晶体的能带结构是通过色散关系ω(k)来描述,这里k取值位于简约布里渊区,在一维情况下即为-π/d≤k≤π/d,d是空间周期。在时变光子晶体中空间周期变为时间周期,能带结构将通过色散关系k(ω)来描述,ω位于简约布里渊区0≤ω≤2π/T。根据周期结构的布洛赫原理,在相距一个周期的两个界面上,电场的二元矩阵满足以下关系
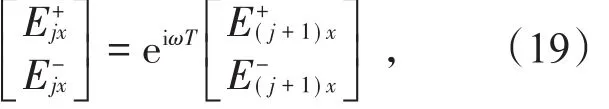
j表示周期数。同时

结合两式有

这是一个矩阵本征值方程,eiωT是其中一个本征值,另一个本征值是其复共轭。根据矩阵本征方程性质,有
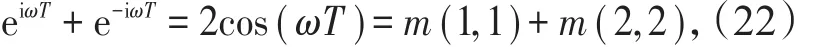
(22)是关于ω和k的隐式方程,数值求解该隐式方程可得到ω和k的色散关系。
2 计算和分析
针对图1的结构模型,使用上节的传输矩阵方法计算时变光子晶体的透射谱。模型参数T1=T2=1 s、n0=1、n1=1.5、n2=3、N=10,空间波数基本单位为k0=2π/(cT),结果如图2所示。本文中称ω为时间频率,k为空间频率,则空变光子晶体透射谱是时间频率的函数,而时变光子晶体透射谱是空间频率的函数。光子晶体的透射谱是电磁波干涉的结果,电磁波干涉取决于电磁波相位的叠加。电磁波相位包含空间相位kz和时间相位ωt两个部分。空变光子晶体波数呈空间分布,与频率有关,频率决定总相位变化,因此是时间频率谱。时变光子晶体频率呈时间分布,与波数有关,波数决定总相位变化,因此是空间频率谱。图2显示明显的带隙特征,在k/k0=1、2、4、5处是带隙中心。经观察发现,通带中心位于k/k0等于n1的整数倍处(k/k0=N1n1,N1是整数)。这是因为

在T1时间段满足共振条件。注意k/k0等于3的整数倍时,带宽最大,这是因为

在T1和T2两个时间段均满足共振条件。
空变光子晶体由于材料折射率离散空间的平移对称性,产生时间频率带隙,实现对时间频率的控制;时变光子晶体由于材料折射率离散时间的平移对称性,产生空间频率带隙。空间频率透射谱的意义在于对电磁波空间频率k也即波长的控制。空间频率带隙结构决定了什么波长的电磁波才能传播、什么波长的电磁波会被反射。由于平移对称性的不同,光子晶体将实现对电磁波不同时空属性的控制。
对无穷周期,可通过求解隐式方程(22)得到色散关系k(ω),根据上述参数计算结果如图3所示。很明显,在k/k0=1、2处出现2个带隙(阴影部分),结果与透射谱一致。当然上述传输矩阵方法适用条件是折射率时变为阶跃型情况。对折射率渐变情况需要采取另外的方法。

图2 时变光子晶体的透射谱

图3 无穷周期时变光子晶体的色散
3 结论
本文结合空变光子晶体的研究方法推导出了时变光子晶体计算的传输矩阵方法。利用该方法可以计算折射率阶跃型时变光子晶体的空间频率透射谱和能带结构。该研究对设计时变光子晶体控制电磁波传输有一定指导意义。

