奇点指数计算的新方法

王义成，肖海箭，龚丽亚

（安徽大学数学科学学院，安徽合肥230601）

奇点指数是微分方程定性理论中用于刻画奇点拓扑性质的一个标量，是一个整数。文献[1]证明了著名的Poincaré指数定理，文献[2]给出了经典的Bendixson环域公式

奇点指数计算公式大多是基于一般的Cauchy指标计算方法[3-6]。本文依据互素多项式中的一个基本代数定理[7-8]，巧妙地构造了一个特殊的齐次多项式，并运用指数的几何意义，得到了一种新的计算指数的简单方法，它不同于Cauchy指标计算方式，比Cauchy指标计算法更加简单有效。

定义1[1]设

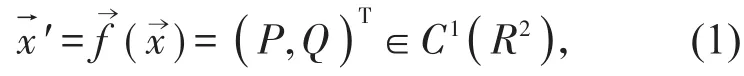
若C为R2上若尔当闭曲线，且曲线C上不存在奇点，定义此曲线指数为正整数，即

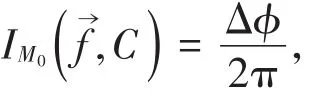
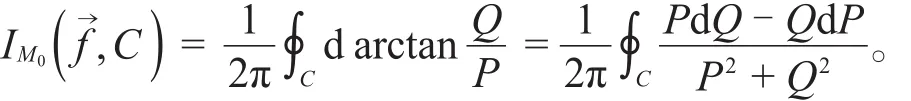
注 如果任意若尔当曲线C仅仅包含单奇点M0，则IM0(, C )与M0的指数是相同的，因此去掉标记C，并记IM0()是该奇点M0的指数。不失一般性，假定这个单奇点是原点O(0 ,0)。

现介绍与本文相关的几个重要引理和命题。

引理1[1]如果原点是(1)式的孤立奇点，则对任意的a≠0，有IO(a P,Q ) =sgna·IO(P ,Q)。

引理2[2]如果原点是(1)式的一个孤立奇点，则IO(P ,Q ) =-IO(Q ,P)。

引理3[2]如果原点是(1)式的一个孤立奇点，则IO(P +Q,Q ) =IO(P ,Q)。

引理4[6]设→∈ C1(R2)，原点O( 0 ,0)是这两个系统的孤立奇点，如果对于一个若尔当曲线C⊂U( O )，其中U( O )是原点的一个邻域，在f→与g→相反的方向，并没有曲线C上的点，则=IO(→ )。

引理5[9]设f和g分别是阶数为m和n的实多项式，如果f和g是互素的，则存在两个多项式u和v，使得

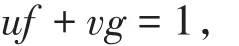
其中多项式u和v的阶数分别为∂u和∂v，且∂u＜n和∂v＜m。

引理6[10]对于若尔当曲线C⊂U( O )，其中U( O )是原点的一个邻域。在曲线C上，如果p是的倍数，p的变化范围为( + ∞,-∞ )，且其倍数的变化范围为(+ ∞,-∞ )，则有

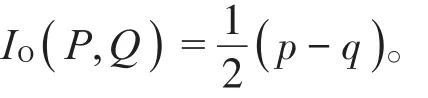
命 题 1 设 ai,bi∈R,i=1,2，如 果sgn( a1b2-a2b1)≠0，

则

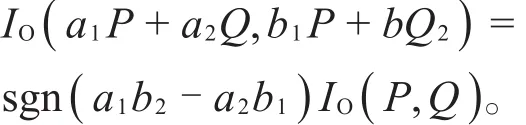
证明 仅证明a1a2b1b2≠0的情形，其余情形类似。

由引理1、2和引理3，可以得到

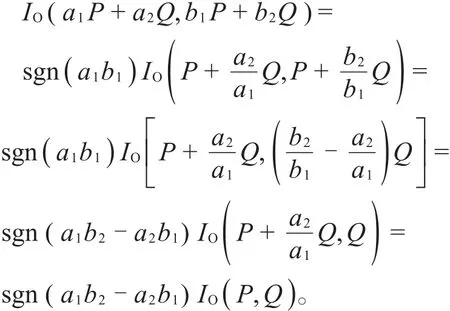
证明 由定义1计算得

对于实平面自治微分系统

如果原点是（2）式和（3）式的孤立奇点，则由引理 4 可得 IO(f→)=IO(g→ )。下面给出本文的主要结论。

定理 1 设mn=1，如果det Dg→( )0,0 ≠0，则

证明 由定理1的假设可知原点是（2）式和（3）式的孤立奇点，因此IO()=IO(→ )。 应用命

题1，则 有 IO() =sgn(d et D( 0 ,0 ) )IO(x ,y ) =sgn(d et D(0 ,0 ) )。

定理2设mn＞1，同上如果原点是（2）式和（3）式的孤立奇点，则通过有限次迭代，可求得IO(g → )的值。

证明 由引理5可知，存在两个多项式u(t)和 v(t) ，其 中 ∂u＜n 和 ∂v＜m ，使 得u(t) P(t ,1 ) +v(t) Q( t ,1 ) =1。设

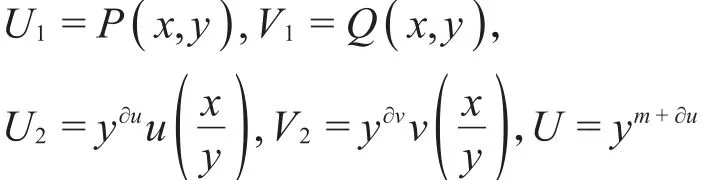
且

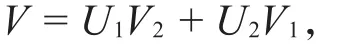
在命题2中，可以证明IO(U ,V ) =IO( U1,V1)+IO( U2,V2)。IO( U ,V)可以直接计算出来，因为U=ym+∂u是一个特殊的齐次多项式，从P2( t ,1 ) +Q2( t ,1 ) ≠0得到V( ± a,0 ) ≠0，其中a＞0,a→0。令C是条二次曲线，在点x=±a,y=±a，起于点( a ,a)并绕向正方向，由引理6可以得到如表1所示结果。

表1 当m+∂u分别为偶数、奇数时奇点的指数

作为定理的应用，给出以下例题加以说明。

例 计算如下系统的奇点指数

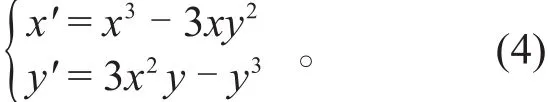
解 显然原点是该系统的孤立奇点，设

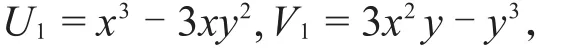
显然U2和V2可由表示。由m+∂u=5和V( a ,0 ) =-a5≠0知，对于任意a＞0,a～0有IO(U ,V ) =1。不失一般性，假设由m+∂u=3和V( a ,0 ) =a3≠0知，对于任意a＞0,a～0有IO(U ,V ) =-1。同时，由定理1可知，IO(U2,V2)=1，因此，综上可知IO(x3-3xy2,3x2y-y3)=3。