三个高阶伯努利多项式与等幂和多项式的对称等式
伍 鸣
(金陵科技学院公共基础课部,江苏 南京 211169)
伯努利数是18世纪瑞士数学家雅各布·伯努利引入的一类数,它在理论上和实际中都具有重要意义。1713年,雅各布的巨著《猜度术》出版,是组合数学及概率论史的一件大事,书中给出的伯努利数有很多应用。组合数学中,伯努利数与数列和的计算有着紧密联系,一直被数学研究者广泛研究。不仅如此,伯努利数在数论中地位也很重要,它曾被用于费马大定理的论证中。
近年来,有关伯努利数与伯努利多项式卷积表达式的相关研究[1-3]越来越受人们关注,其中包含等幂和的伯努利数与伯努利多项式表达成为了一个新的亮点。
1 伯努利数的基本对称等式
伯努利数Bn由指数生成函数
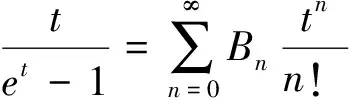
(1)

与此同时,伯努利多项式Bn(x)也由指数生成函数

(2)
对任意整数k≥0,Sk(n)=0k+1k+…+nk被称为等幂和多项式,Sk(n)与伯努利数Bn有着如下重要关系[4]:

(3)


(4)
Deeba、Rodriguez[5]和Gessel[6]分别证明了对一切正整数n和a,下述等式成立:

(5)
Tuenter[7]发现了一个关于伯努利数与等幂和多项式的对称关系式,同时指出等式(5)恰好是这个对称关系式的特例。这个对称关系式如下:
引理1对任意正整数a,b以及n≥0,

(6)
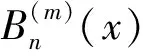
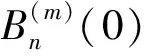
Yang[8]证明了一个高阶伯努利多项式与等幂和多项式的对称关系式如下:
引理2对任意正整数a,b,m以及n≥0,

(7)
2 含幂和多项式的伯努利多项式对称式
定理1对任意正整数a,b,c,m,以及n≥0,



类似于上述方法,同样有

以及
通过对比这些展开式中tn/n!的系数,容易得出结果。 证毕。
推论1对任意正整数a,b,c,以及n≥0,
证明在定理1中,让m=1,z=0,即得。 证毕。
很明显,等式(6)和(7)恰好是推论1与定理1的特殊情况。
推论2对任意正整数a,b,c,m以及n≥0,
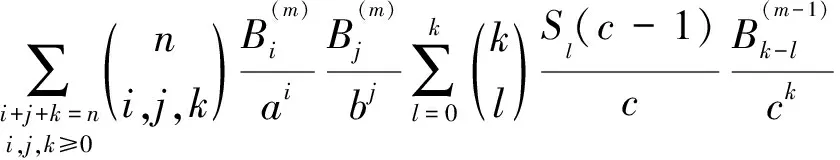
证明在定理1中,让x=y=z=0,即得。 证毕。
定理2对任意正整数a,b,c,m以及n≥0,有



同样可得
以及
比较最后几个方程右端中tn/n!的系数,容易得出结果。 证毕。
3 结 语
本文在Tuenter和Yang工作的基础上,推广了一个关于伯努利数与等幂和多项式的对称关系式,获得了关于三个高阶伯努利多项式与等幂和多项式的对称等式,它将已有的结果都包含在这一等式中,并且得到了伯努利多项式乘法定理的推广形式。
[1] Dilcher K. Sums of Products of Bernoulli numbers[J]. Journal of Number Theory,1996,60:23-41
[2] Satoh J. Sums of Products of Two q-Bernoulli Numbers[J]. Journal of Number Theory,1999,74:173-180
[3] Wu M, Pan H. Sums of Products of Bernoulli Numbers of the Second Kind[J].The Fibonacci Quarterly, 2007,45:146-150
[4] Comtet L.Advanced Combinatories[M].Reidel:Dordrecht,1974
[5] Deeba E, Rodriguez D. Stirling’s Series and Bernoulli Numbers[J].The American Mathematical Monthly,1991,98:423-426
[6] Gessel I. Solution to Problem E3237[J].The American Mathematical Monthly,1989,96:364
[7] Tuenter H J H.A Symmetry of Power Sum Polynomials and Bernoulli Numbers[J].The American Mathematical Monthly, 2001,108:258-261
[8] Yang S L. An Identity of Symmetry for the Bernoulli Polynomials[J].Discrete Mathematics,2008,308:550-554

