关于伯努利方程的一种新解法

(武汉船舶职业技术学院，湖北武汉 430050)

关于伯努利方程的解法常用的有换元法、常数变易法、变量代换法、积分因子法等.

本文提出了变量代换法的一种新方法，由于变量代换法本质上是常数变易法的扩展应用，所以本文先介绍常数变易法，再给出变量代换法。

方程

叫做伯努利(Bernoulli)方程，其中“P(x)、Q(x)”为x的连续函数。它既不是一阶齐次，也不是一阶非齐次线性微分方程。

1 常数变易法

伯努利方程

对应的一阶齐次线性微分方程

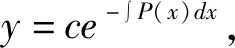
(1)

是伯努利方程的解，则

(2)

将(1)(2)代入到伯努利方程，得

即

是可分类变量的微分方程，即

两边积分

(3)

将(3)式代入(1)式，则伯努利方程的通解为

设y=u(x)x4是原方程的解，将其代入原方程有

则

所以原方程的通解为

2 变量代换法

变量代换法本质上就是常数变易法的变形解法

以下用变量代换法解伯努利方程

方法一：设y=u(x)v(x)是伯努利方程的解，则

y′=u′(x)v(x)+u(x)v′(x)

代入伯努利方程得

u′(x)v(x)+u(x)[v′(x)+P(x)v(x)]=

Q(x)un(x)vn(x)

(4)

令

v′(x)+P(x)v(x)=0

得

(5)

将(5)式代入(4)得

即

故伯努利方程的通解为

例2 求方程y′-3xy=xy2的通解

解：设y=uv是方程的解，则y′=u′v+uv′代入方程得

u′v+u(v′-3xv)=xu2v2

(6)

令

v′-3xv=0

得

(7)

将(7)式代入(6)得

则

所以原方程的通解为

代入伯努利方程得

u′v-u[v′-P(x)v]=Q(x)unv2-n

(8)

令

v′-P(x)v=0

得

(9)

将(9)式代入(8)得

即

故伯努利方程的通解为

(10)

令

得

(11)

将(11)式代入(10)得

则

u-3=e-x(-1-2x)+c

所以原方程的通解为

y-3=-1-2x+cex

方法三(新方法)：设y=u(x)ev(x)是伯努利方程的解，则

y′=u′ev+uevv′

代入伯努利方程得

u′+u[v′+P(x)]=Q(x)une(n-1)v

(12)

令

v′+P(x)=0

得

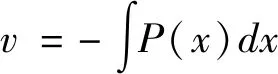
(13)

将(13)式代入(12)得

即

故伯努利方程的通解为

例4 求方程y′-y=xy5的通解

解：设y=u(x)ev(x)是方程的解，则y′=u′ev+uevv′代入方程得

u′+u(v′-1)=xu5e4v

(14)

令

v′-1=0

得

v=x

(15)

将(15)式代入(14)得

u-5u′=xe4x

则

3 结 论

通过对伯努利方程解法的探讨，对我们教育教学提供了新思路，新方法三拓展了解伯努利方程新的思路，为学生掌握相关知识提供了新方法。