“管理决策”课程中“TOPSIS法”教学探讨
陈海文
(安庆师范大学计算机与信息学院,安徽安庆246133)
管理就是决策,决策活动无处不在,它贯穿于社会活动的各个领域,TOPSIS[1-3](Technique for Order Preference by Similarity to an Ideal Solution)法是C.L.Hwang和K.Yoon于1981年首次提出,由于其易理解、操作方便和决策科学等优点,已成为一种重要的决策方法。让管理类专业学生熟练掌握并灵活运用TOPSIS法是“管理决策”课程教学的基本目标。在教学中,发现学生虽能快速掌握基本TOPSIS法的计算逻辑,但对TOPSIS法原理的理解不够深入,在TOPSIS法运用时不能举一反三。为了发散学生的思维,从日常生活中的常见决策问题入手,在讲解基本TOPSIS法的原理和计算逻辑的基础上,介绍了一种新的TOPSIS法,通过比较教学,加深学生对TOPSIS法原理的理解,培养学生的创新意识。
1 基本的TOPSIS法
TOPSIS法是一种枯燥的数学方法,为了使学生对枯燥的TOPSIS法产生浓厚的兴趣,上课伊始,从学生日常生活中的决策问题入手。某同学准备购买1支钢笔,超市里有4支不同款式的钢笔可供他选择,他选择哪支钢笔,这就是现实生活中常见的决策问题。影响该决策的因素有很多,主要有钢笔的颜色、质量、价格、外型和实用性等指标,因为不同的钢笔在不同指标方面的表现不一样,这就让我们难以决策。
在上述决策问题中,如果哪支钢笔的颜色最好看、质量最好、价格最便宜、外形最美观且实用性最强,那么它就是我们心目中最理想的钢笔,反之,它就是我们心目中最不理想的钢笔。这两种理想的钢笔虽然实际上可能不存在,但对于指导我们决策是有帮助的,因为如果哪支实际钢笔的指标值最接近于最理想的钢笔,同时它又最远离最不理想的钢笔,那么它就是本次决策中的最佳钢笔,这就是TOPSIS法的基本原理。
TOPSIS法是一种简单且合乎逻辑的多因素优选方法,其基本思想:确定一个实际可能不存在的最理想方案和最不理想方案,然后计算现实中的每个方案距离最理想方案和最不理想方案的距离(欧几里得距离),最后利用理想解的相对接近度作为综合评估的标准。
设有m个方案,n个评价指标,aij表示第i个方案相对于第j个指标的评价值,则备选方案的指标评价矩阵为A=( aij)m×n,TOPSIS法的具体求解步骤[3]如下:
(1)将矩阵A进行归一化处理得到规范决策矩阵B=(bij)m×n,其中
(2)决策者根据自己的目的和要求将指标重要性的权重确定为wj;
(3)得到方案的指标加权评价值矩阵V=(vij)m×n,其中vij=bij·wj;
(4)确定最理想方案A+和最不理想方案A-:
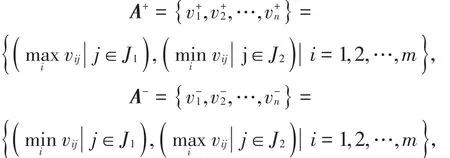
其中J1是表示效益指标的集合,J2是表示成本指标的集合;
(5)计算每一个方案和最理想方案及最不理想方案的欧几里得距离:
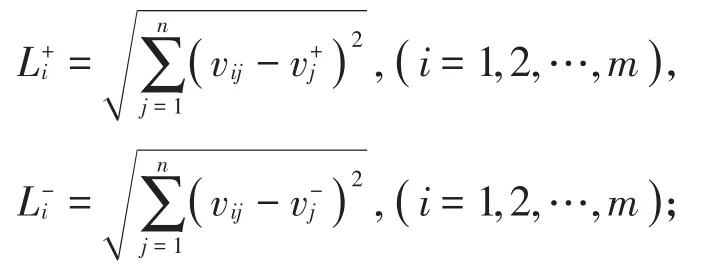
(6)计算每一个方案的TOPSIS评价值,并根据评价值Yi对合作伙伴进行排序优选,Yi=,其中Yi的值越大,表明方案越优。
2 TOPSIS法的变式
在讲解完基本TOPSIS法的基础上,为了发散学生的思维,提问:上述TOPSIS法的计算步骤是否可以改动?经过分析,发现TOPSIS法寻求最佳方案的本质是比较各方案与理想方案间的相似程度,方案间的相似程度仅用距离公式来衡量不够科学,因为距离只能描述向量的大小,而向量是矢量,它不仅具有大小特征,还具备方向特征,因此应该运用向量相似度[4-6]来衡量方案间的相似程度,于是引导学生运用向量相似度对基本TOPSIS法进行修正,从而让学生真正理解TOPSIS法的基本思想。
在运用向量相似度时,需要对基本TOPSIS法的第(5)步和第(6)步作如下调整:
对于第i个方案Li=(vi1,vi2,…,vin),它与最理想方案A+={,,…,}及最不理想方案A-={,,…,}之间的相似度分别为
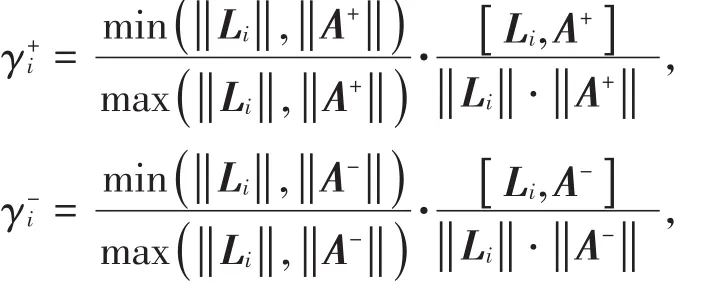
其中‖Li‖、‖A+‖和‖A-‖分别表示向量Li、A+和A-的模,[ Li,A+]、[ Li,A-]分别表示向量Li与A+、向量Li与A-的数量积;
由于向量间的相似度和向量间的距离是两个相反意义的量,所以方案的TOPSIS评价值Yi的计算公式应修正为,其中Yi的值越大,表明方案越优。
3 TOPSIS法的实践教学
为了提高学生的动手能力,达到学以致用的目的,让学生编程实现两种TOPSIS法,并分别运用两种TOPSIS法对引例中的问题进行决策,加深学生对两种TOPSIS法的理解和运用。为了反映这些指标在该同学心目中的地位,让该同学对这些指标进行评判,给出指标的权重向量w=(颜色,质量,价格,外型,实用性)=(0.15,0.3,0.3,0.15,0.1),紧接着,让该同学对这4款钢笔进行打分评判,由于该决策问题较简单,采用常见的10分制,评判结果如表1所示。
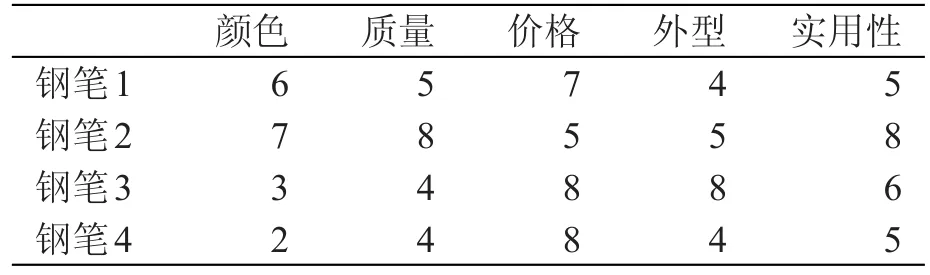
表1 钢笔原始评判数据表
得到原始评判数据后,运用归一化公式对原始数据进行处理,归一化后的结果如表2所示。
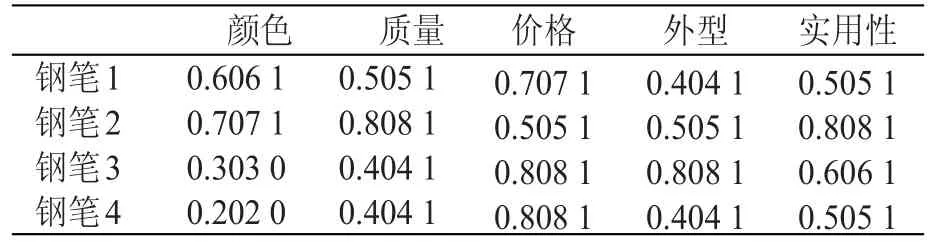
表2 归一化结果表
紧接着,让学生根据指标的权重向量,运用公式vij=bij·wj计算出加权评判矩阵,结果如表3所示。
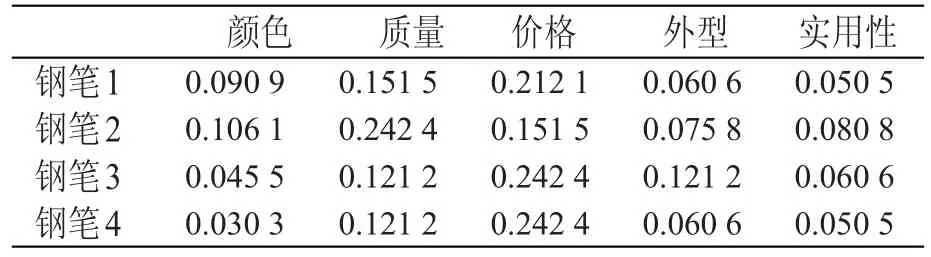
钢笔1钢笔2钢笔3钢笔4颜色0.090 9 0.106 1 0.045 5 0.030 3质量0.151 5 0.242 4 0.121 2 0.121 2价格0.212 1 0.151 5 0.242 4 0.242 4外型0.060 6 0.075 8 0.121 2 0.060 6实用性0.050 5 0.080 8 0.060 6 0.050 5
在上述加权评判矩阵中,可以找出最理想的钢笔和最不理想的钢笔,最理想的钢笔对应的评判向量是(0.106 1,0.242 4,0.242 4,0.121 2,0.080 8),最不理想的钢笔对应的评判向量是(0.030 3,0.121 2,0.151 5,0.060 6,0.050 5)。在完成上述工作的基础上,让学生分别运用两种TOPSIS法对该问题进行决策分析,决策结果分别如表4所示。
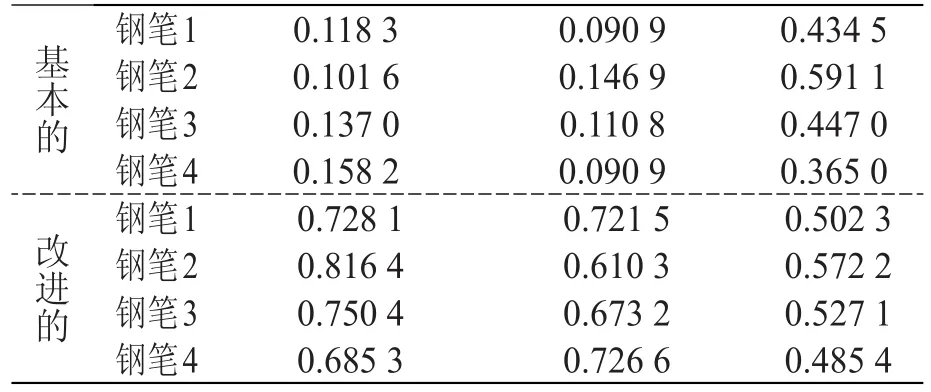
表4 基本的TOPSIS法与改进的TOPSIS法决策结果
与最理想钢笔间的距离与最不理想钢笔间的距离
TOPSIS值
为了加深学生对两种TOPSIS法的理解,提高学生的动手能力,让学生自己编程[7-8]实现上述过程,两种TOPSIS法的决策结果分别如图1和图2所示。
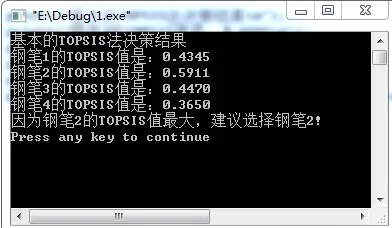
图1 基本的TOPSIS法决策结果图
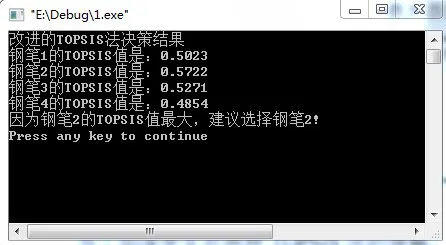
图2 改进的TOPSIS法决策结果图
从两种TOPSIS法的决策结果来看,改进的TOPSIS法的决策结果和基本的TOPSIS法的决策结果是一致的,这表明改进的TOPSIS法是有效的、正确的。
4 结束语
TOPSIS法是管理决策中一种重要的决策方法,因其有效性和易操作性,我们在教学过程中必须理论联系实际,让学生熟练掌握该方法。采用比较教学的方式,既加深了学生对TOPSIS法原理的理解,也培养了学生的创新意识,为类似课程的学习提供了借鉴。让学生自己编程实现TOPSIS法可提高学生的实践动手能力,有利于培养学生的综合素质,为学生以后走上工作岗位打下坚实的基础。

