基于Floyd算法的最短路径优化研究

邱晓鹏，王丽君

(1.陇南师范高等专科学校 数信学院，甘肃 成县 742500；2.陇南师范高等专科学校 电子商务学院，甘肃 成县 742500)

0 引言

研究最短路径的算法比较多，像Dijkstra、Bellman-Ford和Floyd算法等，其算法优化问题是一个研究热点.在多源最短路径算法基础上，相对于Dijkstra和Bellman-Ford算法，Floyd算法是一种更快的算法，也是比较简单的算法.但在某些情况下,Floyd算法解决实际问题时，会发现算法的执行时间只能勉强达到时间限制要求.优化改进后的算法在时间复杂度和空间复杂度上都有所降低.

1 Floyd算法分析

1.1 路径中的途经点

假设有连接两个顶点u和v的路径.此路径肯定会经过起点u和终点v，此外还会经过其他顶点.比如，没有直接连接u和v的路径，或者经过其他顶点的路径比直接连接的路径更短，此时就会经过其他顶点.路径经过的顶点就成为途经点.

只将顶点集合S中的顶点用作途经点得到的从u到v的最短距离，记作DS(u,v).例如，图1的拓扑图中，D{}(a,b)=5，而D{c,d}(a,b)=4.如果不需要使用S中的所有顶点，则有D{a,c,d,e,g,f}(b,f)=D{}(b,f)=3.使用这种标记法时，最终想得到的结果值是将整个顶点的集合V都用作途经点的DV(u,v).连接两个顶点的边线中,最短边线的长度w(u,v)等于D{}(u,v).

假设有以S中的顶点为途经点而得到的从u到v的最短路径.选择S中的顶点之一并标为x.此时，有两种形态，路径不经过x：此路径只将S-{x}中的顶点用作途经点；路径经过x：此时，路径可分为u到x的区间和x到v的区间.这两个子路径必须是连接u和x、x和v的最短路径.很显然，两个子路径并不会途经x，所以只会将S-{x}中的顶点用作途径点.

将S用作途经点的从u到v的最短路径会选择上述路径中较短的一个，因此，可以把Ds(u,v)按照归方式定义为如下形式.

Floyd算法会计算出图1部分拓扑图的所有成对顶点之间的最短距离，并保存到二维数组tpt[][]中，此数组的元素tpt[u][v]表示从顶点u到v的最短距离.其运算方式不同于迪杰斯特拉算法(Dijkstra)[1]和贝尔曼-福特算法(Bellman-Ford)[2].迪杰斯特拉算法和贝尔曼-福特算法都是从一个起点出发，计算到各顶点的距离.不过，根据问题的需求，有时候需要对所有成对顶点求出最短距离.要解决此问题，可以用迪杰斯特拉算法，只要把各顶点都视为起点，并反复执行迪杰斯特拉算法即可实现.若存在负权值，就改用贝尔曼-福特算法.这样就会大大增加时间和空间复杂度.其实，想要对所有成对顶点求出最短距离，Floyd多源最短路径算法是一种更快的算法[3]，更是最简单的算法.而且已有现成的Floyd算法的原型.

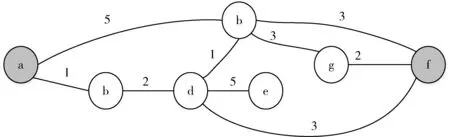
图1 拓扑图

1.2 Floyd算法的原型

简单修改上述递归式，就能利用动态规划法[4]解决多源最短路径问题.设Sk={0,1,2,…,k}，Ck=DSk.那么，Ck(u,v)就等于只把0到k的顶点用作途经点时，得到从u到v的最短距离.利用此标记法就能把上述递归式改写为如下形式.

递归式中，Ck的所有值只依赖于Ck-1，所以利用选代动态规划法就非常容易求解.代码1-1是实现这种方法的代码.此代码中，Ck(u,v)的值会保存到C[k][u][v].因此，函数终止运行后，若想知道u到v的最短距离，只需查看C[V-1][u][v]即可.

代码1-1Floyd算法的原型

int v;

int tpt[MAX_V] [MAX_V];

int C [MAX_V] [MAX_V] [MAX_V];

vold allPairShortestPath1(){

for(int i=0;i

for(int j=0;j

if(i!=j)

C[0][i][j]=min (tpt[i][j], tpt[i][0], tpt[0][j]);

else

C[0][i][j]=0

for(int k= 1：k

for(int i=0：i

for(int j=0;j

C[k][i][j]=min (tpt[k-1][i][j], tpt[k-1] [i][k], tpt[k-1] [k][j]);

}

要注意，计算C(0)时，C[0][u][v]总是会初始化为0，因为即使没有额外到达自己本身的边线，其最短距离也会是0.显而易见此算法的时间复杂度也由三重for循环语句决定，每个for语句会执行O(|V|)次，所以整个算法的时间复杂度是O(|V|3).

2 Floyd算法内存使用量的优化

Floyd最短路径算法在此基础上更进一步，在不使用额外数组的前提下，在保存图结构加权值的邻接矩阵中计算递归式的结果值.利用滑动窗口就能把此代码的内存使用量减少至O(|V|2).只要有Ck-1就能求出Ck的值，所以没有必要继续保存Ck-2、Ck-3等的结果值.利用这一特点就能把代码1-1中的数组大小减少至2×|V|×|V|.因为，只需要把Ck(u,v)的值保存到C[k%2][u][v]即可.

代码1-1使用过的递归式中，为了计算出Ck(u,v)，需要的只是Ck-1(u,k)和Ck-1(k,v).而Ck-1(u,k)和Ck(u,k)区别如下：1、Ck-1(u,k)=把起点到第k-1个顶点用作途经点的从u到k的最小长度；2、Ck(u,k)=把起点到第k个顶点用作途经点的从u到k的最小长度.

可以确定起点或终点是第k个顶点时，把k添加到可使用途经点的目录将没有任何意义.这就等于，“经过地铁站到达63大厦的路径”和“经过地铁站和63大厦到达63大厦的路径”并没有什么区别.由此可知，不用区分Ck-1和Ck的值，可以直接混用.因此，不用区分C[k%2]和C[(k-1)%2]，而可以直接在同一二维数组中混用.

代码4-1的Floyd算法根本不生成额外的数组C，而直接在邻接矩阵tpt中计算最短距离.此算法的时间复杂度还是O(|V|3)、而空间复杂度减少到了O(|V|2).通过图结构的邻接矩阵表示法，tpt[u][v]等于从u到v的边线加权值.若没有边线，就代入极大值.

代码4-1-Floyd算法的实现方法

int v;

int tpt[MAX_V] [MAX_V];

vold floyd(){

for(int i=0;i

for(int k=0;k

for(int i=0;i

for(int j=0;j

tpt[i][j]= min (tpt[i][j], tpt[i][k]+ tpt[k][j]);

}

3 Floyd算法执行优化

某些情况下利用Floyd算法解决实际问题时，会发现该算法的执行时间只能勉强达到时间限制要求.对于这种情况，可以在不改变时间复杂度的前提下，依然能对算法进行优化，那就是在第二个for语句之后，确认从i到k的路径是否实际存在.如果从i到k的路径不存在，就没有必要对j执行for语句.这样会大大降低了运算时间，巧妙地优化了Floyd算法.

4 Floyd优化改进算法的实现

Floyd算法的执行方式不同于向最短路径逐条添加边线的迪杰斯特拉算法和贝尔曼-福特算法，所以计算实际路径的过程也大不相同.执行Floyd算法后，为了计算两个顶点之间的最短路径，需要把各成对顶点u、v最后一次更新tpt[u][v]时使用过的k值保存起来.假设此顶点的序号为w.经过此顶点后，tpt[u][v]变为最小值，这就意味着u到v的最短路径会经过w.因此，利用递归调用的方式就能找出u到w的最短路径和w到v的最短路径.最后，将这两个最短路径相加就能得到u到v的最短路径.

代码4-1表示求最短路径时额外计算所需附加信息的算法，以及计算实际路径的函数源代码.此代码只额外利用O(|V|2)内存就能计算最短路径.

代码4-1 Floyd算法的改进算法

//顶点个数

int v;

//图结构的邻接矩阵表示法

//tpt[u][v]=从u到v的边线加权值.若没有边线，就代入极大值.

int tpt[MAX_V] [MAX_V];

//tpt[u][v]=u到v的最短路径经过的顶点中序号最大的顶点

//初始化为-1

int via [MAX_V] [MAX_V];

void floyd2(){

for(int i=0;i

memset(via, -1,sizeof(via));

for(int k= 0：k

for(int i=0;i

for(int j=0;j

if(tpt[i][j]> tpt[i][k]+ tpt[k][j]){

via[i][j]=k

tpt[i][j]= tpt[i][k]+ tpt[k][j]

}

}

//计算u到y的最短路径,并保存到path

void reconstruct(int u, int v, vector& path){

//初始部分

if(via[u][v]==-1){

path.push _back(u);

if(u!=v) path.Push_ back(v);

}

else {

int w= via[u][v];

reconstruct(u, w, path)

path,pop_back(); // 因w重复,故将其删除.

reconstruct(w, v, path);

}

}

5 结束语

本研究的算法虽然对Floyd算法做了改进，但并没有Floyd算法灵活.Floyd算法的另一个著名应用是，在无权图中计算各顶点之间的到达可能性[5],也就是对所有成对顶点u、v确认是否存在相连路径.把Ck(u，v)的定义变换为，把0到k号顶点用作途经点时，给出是否存在u到v的路径，则有如下递归式.

Ck(u,v)=Ck-1(u,v)||(Ck-1(u,k)&&Ck-1))

这种表示法其实与Floyd算法完全相同，只是把求出最小值的运算替换为or运算，把相加运算替换为and运算.与从所有顶点起始进行宽度优先搜索时的时间复杂度相比，这种方法的时间复杂度并没有什么提高.不过，Floyd算法的简洁性还是使其得到广泛应用.