一种基于LMBP神经网络的图像复原方法

史 颖,亓 慧

(太原师范学院 计算机系，山西 晋中 030619)

0 引言

数字图像处理技术现在被广泛使用，由于图像采集条件和设备的局限性导致低分辨率图像的出现，或者在图像获取过程中由于噪声干扰等因素导致图像失真，而在医学、军事、天文等领域对图像的质量要求往往比较高[1].因此，低质图像的复原技术已经成为数字图像处理领域一个重要的研究方向[2].

反向传播(Back-propagating，BP)神经网络算法是一种常见的图像复原方法，采用反向传播算法，能够逼近任意的非线性映射关系，具有良好的泛化能力[3].但由于其本质是一种反向传递的梯度算法，搜索步长会导致算法的收敛速度很慢，同时容易造成局部极小点[4].

本文从如何加快BP神经网络的收敛速度和收敛性的角度解决图像复原问题，采用数值优化技术改进的算法——LMBP(Levenberg-Marquardt Back Propagating)神经网络算法对图像进行复原[5]，该算法有效结合了神经网络的梯度下降法和高斯牛顿法的优点，对收敛速度和收敛性做了一个折中，既保证了图像复原的效果，又加快了算法运行速度[6].

1 LMBP神经网络算法

LMBP神经网络算法是最优化理论中比较有效的优化方法，它是牛顿法和最速下降法的一种结合算法，对BP神经网络算法收敛速度和收敛性进行了折中.本文采用的LMBP神经网络模型如图1所示.

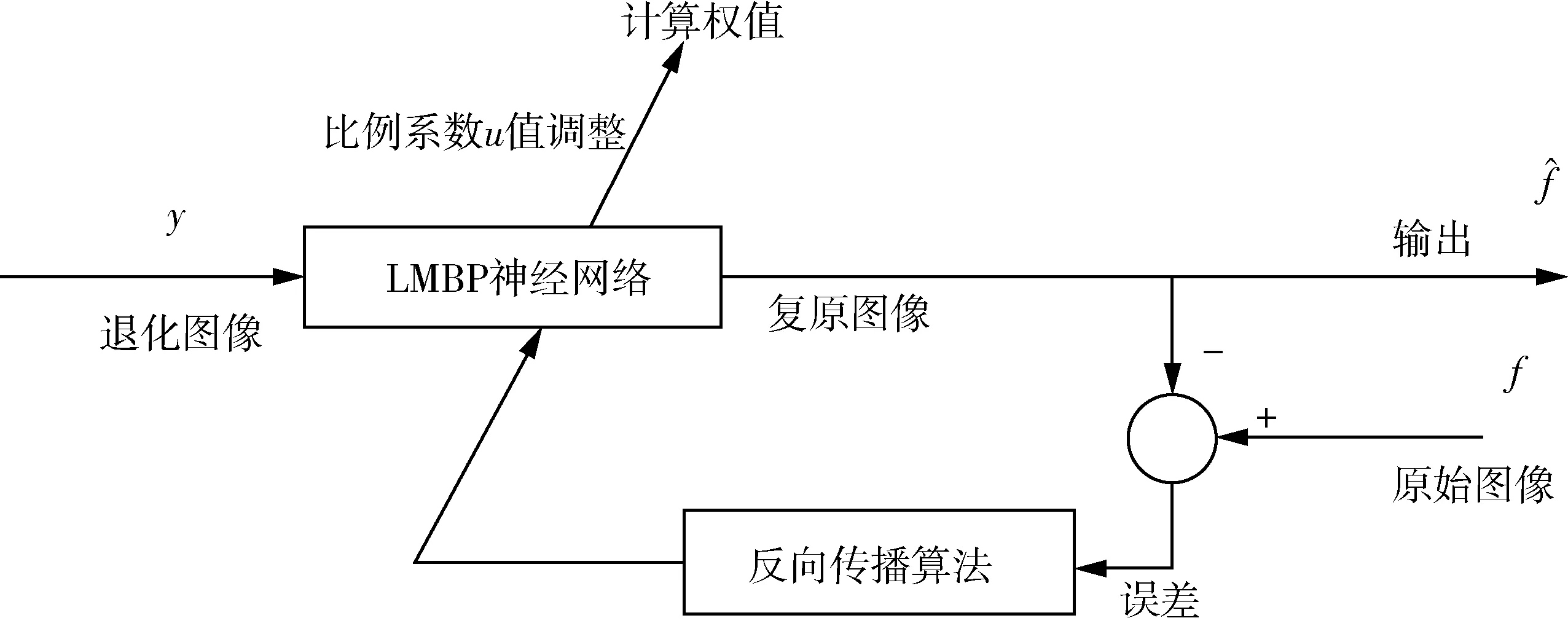
图1 用于图像复原的LMBP神经网络模型

常见的BP神经网络结构包含了输入层、隐含层和输出层[7].主要目的是通过输入输出样本对(Q个){(x1，y1)，(x2，y2)，…(xm,ym)}来调节连接网络的权值向量W，调整误差函数E(w)，保证网络输出与期望输出之间误差最小.在图像复原中可以借鉴BP神经网络的原理[8].将模糊图像或者噪声图像作为样本集进行训练，利用BP神经网络的自学习功能，在不知道点扩展函数的情况下，实现噪声图像和原始图像之间的非线性映射关系，拟合后实现造神噪声的复原[9].图2为常见的BP神经网络结构[10].

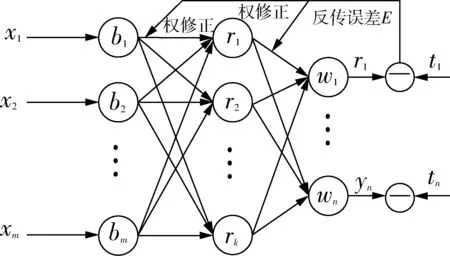
图2 BP神经网络结构

LMBP神经网络是为了加快BP神经网络的收敛速度，引入了高斯牛顿法来求解误差函数E(w)，其梯度函数可由以下公式得到：

ΔW=-[JT(w)J(w)+μI]-1J(w)e(w).

(1)

其中，e(w)为误差向量，J(w)为e(w)的Jacobian矩阵；I为单位矩阵，比例系数μ为大于0的常数[11].

若μ值较大，则LMBP神经网络算法近似于梯度下降法：

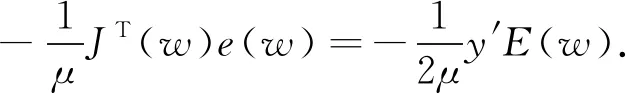
(2)

当μ接近于0时，则为高斯牛顿法.高斯牛顿法在误差E(w)接近最小值时，计算速度更快，精度更高[12].

LMBP神经网络算法

2 实验结果及分析

应用基于LMBP神经网络的方法对图像进行复原，校果见图3、图4.

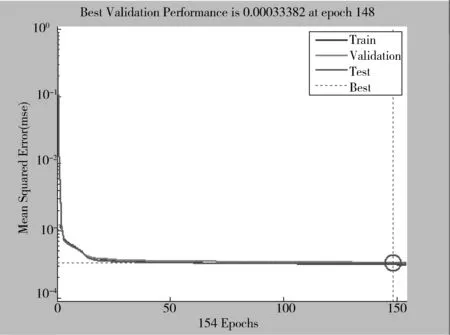
图3 LMBP算法收敛效果

图4 LMBP算法图像复原效果展示

图4显示，LMBP算法在收敛次数为148次时效果最佳.对典型的模糊图像而言，基于LMBP神经网络的图像复原方法复原效果较好.

3 结论

针对图像模糊问题，将高斯牛顿法和反向传播方法用于图像复原.主要应用了LMBP算法，可以兼顾神经网络算法的收敛速度和收敛性能.实验结果表明，应用基于LMBP神经网络算法对图像进行复原效果明显，收敛速度快.

LMBP算法为模糊图像的复原提供了有益的参考.另外，在大数据背景下如何利用神经网络方法实现彩色图像复原是我们未来的工作.