线性代数课程内容的关联性研究与实践
孟小燕 朱铁锋


[摘 要]线性代数是一门重要的工具性课程,其高度抽象性,大量的概念、性质、定理,繁杂的运算给学生学习增加了难度.从课程特点出发,着眼于课程的整体结构,建构知识关联,由此增加教与学的连贯性、系统性,是提高学生理解能力和拓展学生思维的有效途径;在夯实基础的前提下,注重实际问题研究,借助数学软件、数学实验化解计算问题,使抽象概念直观化,均可有效提高线性代数课程的教学质量和效率.
[关键词]线性代数;关联性;整体性;知识结构;教学方法
[中图分类号] G642.3 [文献标识码] A [文章编号] 2095-3437(2019)07-0118-03
线性代数几乎是所有高校理工科及经管专业都会开设的一门专业基础课程.如果说微积分采用“由曲化直”的思想将非线性的问题转化为线性问题,如变速直线运动的路程、弧长、曲边梯形的面积、曲顶柱体的体积等,线性代数则是研究线性问题的重要工具,广泛应用于自然科学和社会科学中,特别是在图形编程与机器学习领域的应用无处不在,对学生后续的专业学习具有重要的基础性意义.从初等数学到线性代数的思维跨度要比高等数学、概率与数理统计大得多.初入大学校门,很多学生不难理解并接受函数、数列、极限、导数等概念,但却对线性代数的各种符号、运算望而生畏.线性代数具有高度的抽象性与逻辑性,根据课程的特点,找到知识内容的逻辑脉络,疏通概念间的关联,将零散的知识点进行整合,并加以分析、总结归纳是促进学生对课程的理解,培养他们良好的逻辑思维能力、分析解决问题能力的重要途径.
一、线性代数课程部分知识内容建构
线性代数的特点之一是概念多、性质定理多、运算规律多、运算量大,各章内容看似相互独立,实则前后知识衔接紧密.以同济大学数学系主编的《工程数学—线性代数》第六版为蓝本,其主要内容包括六部分即行列式、矩阵、线性方程组、向量组的线性相关性、相似矩阵及二次型、线性空间与线性变化,其所使用的研究工具则是矩阵和行列式,这些看似不相关的内容在其表现形式上存在着一一对应的关系[1]:如线性方程组与矩阵,矩阵与向量组,矩阵的秩、初等变换与向量组的秩、线性方程组解的结构,行列式与n元一次线性方程组、方阵、可逆矩阵、特征多项式等.在教学中,教师可以将其中一项内容作为课程内容的出发点,建构与其他各分支的关联,逐层递进,从而形成系统的知识体系,化解抽象概念多的难题.
(一)以线性方程组为出发点,建构线性方程组—矩阵间的知识脉络
由于学生原有的认知结构中已经具备了方程组的知识,二元、三元一次线性方程组的解法学生非常熟悉.因此,将线性方程组的高斯消元法引入课程较符合学生的认知规律.将线性方程组中未知数的系数、常数项按原有的位置顺序保持不变,排成一个数表,进而顺其自然地引入矩阵的概念.通过线性方程组消元法的复习回顾,可以引导学生发现解方程组的过程事实上就是同解变形的过程,而这一过程参与运算的只有未知数的系数和常数项,对应矩阵的三种行变换即对换变换([ri?rj])、倍乘变换([ri×k,k≠0])、倍加变换([rj+kri]),也就是矩阵的初等行变换,与初等列变换一起统称为矩阵的初等变换.通过矩阵的初等变换可以将矩阵化为行阶梯形矩阵,进而化为行最简形矩阵,由此解决求逆矩阵、求矩阵的秩等问题.从矩阵的乘法运算规律出发,又可以将[n]元线性方程组简写成[Ax=b]的形式,其中[A]是方程组的系数矩阵,[x],[b]分别是未知数、常数项所组成的列矩阵,从而利用矩阵初等变换求[A-1]的方法关联解线性方程组;同时可以利用矩阵初等变换求秩的方法与线性方程组[Ax=b]解的结构建立关联.如图1所示.
(二)以行列式为起点,建构行列式—线性方程组、矩阵间的知识脉络
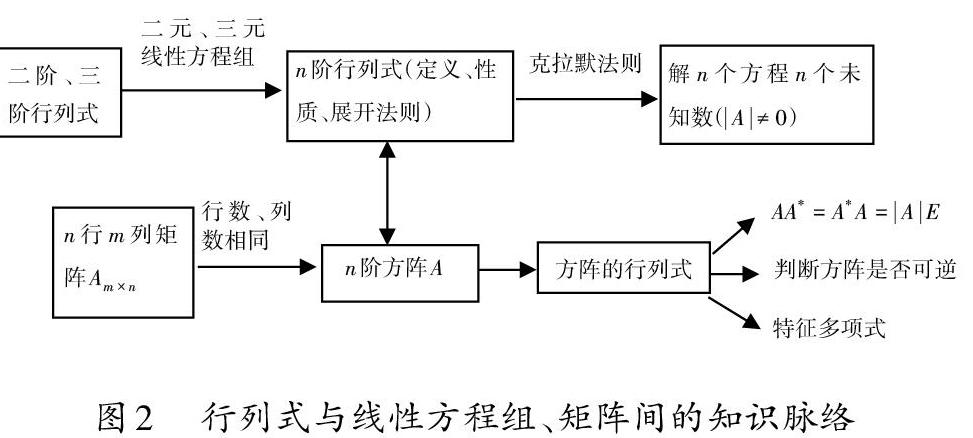
行列式和矩阵都是线性代数中的重要工具.如果说利用矩阵的初等变换可以解决广义的[n]元线性方程组求解问题,那么当遇到方程的个数与未知数的个数相同的情形时,还可以利用行列式来解线性方程组,即用克拉默法则求解.从二阶、三阶行列式引入高阶行列式的定义,进而探讨行列式的性质、展开法则、运算技巧等.行列式的计算并不是课程的主要内容,但作为后续方阵相关运算的铺垫或是[Cramer]法则求解的先导知识,还是需要作为一块独立的内容加以说明.从本质上讲行列式是一个数,矩阵是一个数表,二者本没有什么关联,当矩阵的行数与列数相同时,如果引入[n]阶方阵的概念,矩阵和行列式之间就会建立关联.研究方阵的行列式,利用行列式判断矩阵是否可逆;矩阵乘积的行列式等于行列式的乘积[AB=AB];利用伴随矩阵[A*]求逆矩阵,伴随矩阵[A*]又是由[A]的各个元素的代数余子式[Aij]构成的;求矩阵的特征多项式[A-λE]、求特征根;相似矩阵的行列式值相等;正交矩阵其行列式的值为[±1]等,可以通过梳理各部分知识的关联,帮助学生建立清晰的逻辑结构.如图2所示.
(三)以向量组为起点,构建向量组—矩阵—线性方程组的知识脉络
《向量组的线性相关性》一章涉及的概念非常多,学生接受起来尤其困难.“线性组合”“线性表示”“向量组等价”“线性相关”“线性无关”等概念“如浓浓迷雾滚滚而来”[2],学生深陷其中,茫然不知所云.事实上,向量组、矩阵、线性方程组之间存在着紧密的联系,只要注重内容的整体性,深入浅出地阐明它们之间的关系,便可以有效突破学习内容的重点与难点.
首先是向量组与矩阵间存在一一对应的关系,其实质上就是矩阵按行或按列分块的问题.从分块矩阵的角度按列划分,一个[n]行[m]列矩阵[A]可以看成是含[m]个[n]维列向量的向量组[A:a1,a2,…,am],反之含有有限个向量的向量組总可以构成一个矩阵.明确这一对应关系,对于进一步探讨向量组的线性关系起到重要的铺垫作用.
综上可得,线性方程组[Ax=b]解的结构以及与秩的关系是研究向量组线性相关性的重要基础.线性组合、线性表示可以转化为线性方程组[Ax=b]是否有解的问题;向量组等价可以转换为矩阵方程[Ax=B]是否有解的问题;线性相关、线性无关可以转化为齐次线性方程组[Ax=0]有非零解、有唯一零解的问题;向量组的线性相关性从向量的角度重新刻画了线性方程组的解,并给出其通解的结构,与矩阵的秩三大重要的知识模块相互衔接,彼此渗透,形成一个有机整体,无法割裂开来单独研究.如图3所示.
二、理清知识脉络,把握整体内容格局
纵观各章,可以发现线性方程组及其相关内容是线性代数课程的教学主线.《行列式》一章中克莱姆法则解决的是方程个数等于未知数个数且系数行列式不为零的线性方程组的解;矩阵及其运算中,矩阵乘法为线性方程组提供了一种简洁的表示方法;矩阵的初等变换除给出了广义的线性方程组的求解方法外,同时总结出矩阵的秩与线性方程组解的关联;向量组的线性相关性从向量的视角探讨了线性方程组解的结构;相似矩阵及二次型、线性变换是承接基本概念与典型应用的重要知识点,与前面诸多内容都存在内在联系.
在教学中,教师应采用启发式与参与式教学方法,从宏观上把握教学主线,从微观上引导学生梳理各章节的知识脉络,深入浅出地揭示不同概念、原理间的联系,从而使学生在头脑中逐步建立清晰的知识结构,思维得到拓展,分析处理问题的能力有所提升,有效完成知识、问题间的相互转化,化难为易,增强学习成就感.
三、夯实基础,优化教学方法
学生的学习困惑除来源于线性代数课程中大量的概念、性质、定理、推论以及令他们无法想象的抽象符号外,还来源于他们现有的认识水平很难找到将线性代数用于解决实际问题的情境.在授课中,结合学生所学专业,引入实例,阐明背景,让学生认识到课程的有用性,帮助学生建立正向的学习动机,也是课程教学体系的重要组成部分,而不仅仅是理论、方法的灌输.线性代数课程中烦琐的运算也是令学生望而生畏的原因之一,会影响课堂效率.借助数学软件,既可以解决复杂的计算问题,更能给学生带来更加直观的学习体验。在课程教学中融入计算机技术、数学实验也能激发学生的学习积极性.
四、结语
线性代数是一门重要的基础课程,其抽象性决定了其学习的难度,其广泛的应用性又同时要求学生必须掌握相关知识,做到学以致用.对课程内容的关联性的研究是解决其抽象性的有效路径,同时在夯实基础,明晰课程知识结构的前提下,结合课程内容,注重实例研究,借助数学实验突破学习难题,切实做到教与学有的放矢,这些教学方法都为线性代数教学实践带来巨大推动力,有助于更好地提高课程教学质量和效率.
[ 参 考 文 献 ]
[1] 金英善,贾睿.线性代数教学方法改革实践探索[J].辽宁科技大学学报,2013(5):541-544.
[2] 朱琳,蒋启芬.国外线性代数的教学研究述评[J].数学教育学报,2018(1):79-84.
[3] 同济大学数学系.工程数学线性代数[M].6版.北京:高等教育出版社,2014:81-107.
[4] 江蓉,王守中.矩陣的秩在线性代数中的应用及其教学方法的探讨[J].西南师范大学学报(自然科学版),2012(8):175-180.
[责任编辑:庞丹丹]

