重温知识发展之路，体验自主探索之趣——“点到直线的距离”的溯源之旅

陕西

普通高中课程标实验教科书在数学内容编排上采取了“明确相关内容在不同模块中的要求及其前后联系，注意使学生在已有知识的基础上螺旋上升、逐步提高”的方式，利于学生学习循序渐进、逐步发展，但也导致学生知识支离破碎，不利于构建完整的知识体系.因此，教师应该引导学生以居高临下的态势，以追溯赏析的方式，重温知识的发生发展过程，体验自主探索的乐趣，帮助学生形成完整的知识体系.本文仅以“点到直线的距离”为例，谈谈引导学生经历“溯源之旅”的初步认识.

一、“溯源之旅”案例赏析

1.“溯源之旅”的出发点

在《普通高中课程标实验教科书·数学4(必修)》P99第二章平面向量学习中，教材给出了点到直线的距离公式的向量法证明，记为证法1.

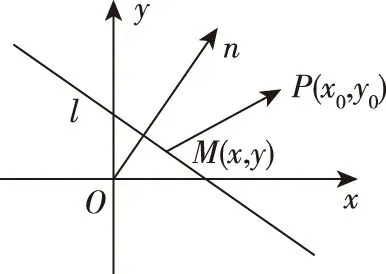
证法1：如图所示，P(x0,y0)是直线外一定点，M(x,y)是直线上任意一点，n0是直线l：Ax+By+C=0的法向量n=(A,B)的单位向量，

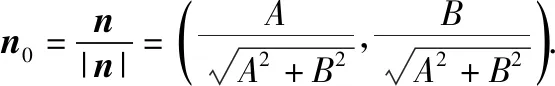
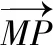
又点M(x,y)为直线l上任意一点，所以C=-(Ax+By),

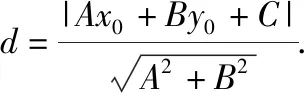
师：这种证法的本质是什么呢？它与直线l上任意一点M(x,y)的选取是否有关呢？

生1：向量法是将点到线的距离问题转化成了直线上任意一点M与给定点P连线的向量在直线法向量上的射影的长度，可简单地说“射影的长即距离”，它与直线上点P的位置无关.

师：既然“射影的长即距离”是该证法的本质，那么是否一定要对直线的法向量单位化呢？

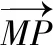
师：能否借助直线l的方向向量，求得点到直线的距离呢？

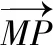
证法2：取直线l的方向向量为v=(B,-A)，则

又点P(x,y)为直线l上任意一点，所以C=-(Ax+By),

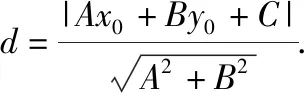
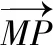
2.“溯源之旅”的追溯点

师：退一步想，求点到直线的距离最朴素、最自然的想法是什么呢？

生4：只需过点P作PH⊥l,垂足为H，先求直线PH的方程，从而可求出交点H的坐标，再用两点间的距离公式求|PH|.

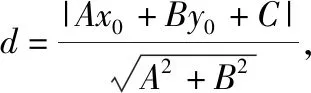
生5：我代表我们小组与大家分享我们组的证明方法，请大家提出宝贵建议.

过点P作PH⊥l于H(a,b)，则直线PH：Bx-Ay=Bx0-Ay0.

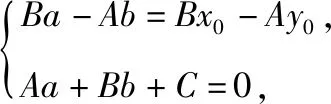
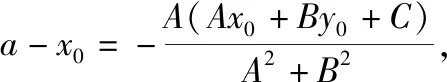
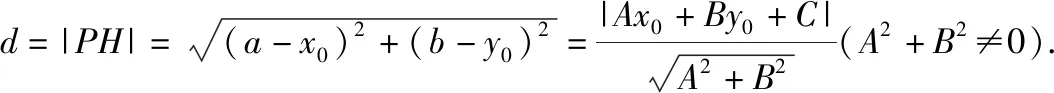
生6：我认为用消元法解方程组时，需要对A，B是否为0进行讨论，同时，只需求得垂足H的横坐标a,再利用A(b-y0)=B(a-x0)直接求得b-y0的表达式更简洁.以下我代表我们组交流我们组的探究成果.

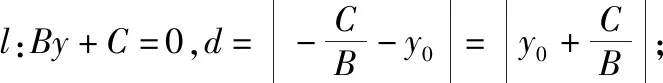
(3)当A≠0,B≠0时，过点P作PH⊥l于H(a,b)，则直线PH：Bx-Ay=Bx0-Ay0.

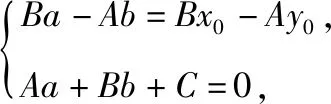
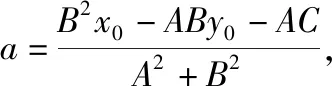
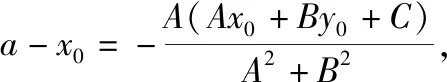
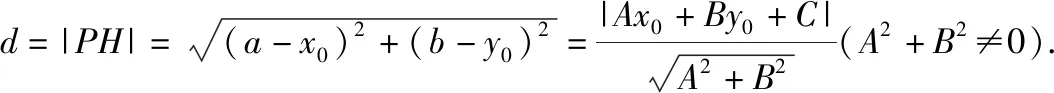
师：上述的方程和计算虽然稍显繁琐，但其中的分类讨论、规范表达和多字母运算的能力训练值得大家重视.当然在具体计算和操作时，必然会受到字母参数过多及运算过程复杂的困扰，这也正是大家能力提升的生长点.

师：证法3中导致运算繁琐的成因是什么？能否对证法作进一步简化呢？

生7：我们组认为，可从条件出发向(a-x0)和(b-y0)靠拢，于是，对第三种类型作如下改进.

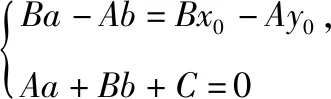
由①2+②2得(A2+B2)(a-x0)2+(A2+B2)(b-y0)2=(Ax0+By0+C)2,

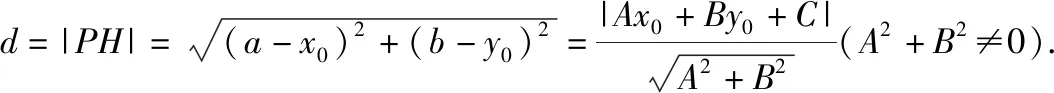
师：我们尤其要注意条件到结论的目标意识和整体代换，证法4的表达和计算方式可能更符合大家的现实能力和水平，也有助于更好的突出条件到目标的指向性，对提升大家方程变形和整体运算能力很有教益.当然，在以上的计算中，也可以利用换元法：

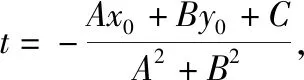
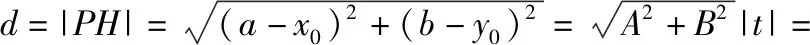
师：证法3、证法4都是利用解析法将几何问题代数化.我们能否利用直角三角形的面积公式来解决点到直线距离的求解呢？

证法5：(3)由A·B≠0知直线l必与两坐标轴相交，如图，作PM∥x轴交直线l于M，作PN∥y轴交直线l于N，作PH⊥l于H，则d=|PH|.

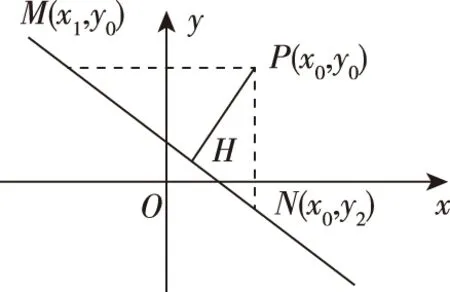
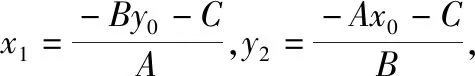
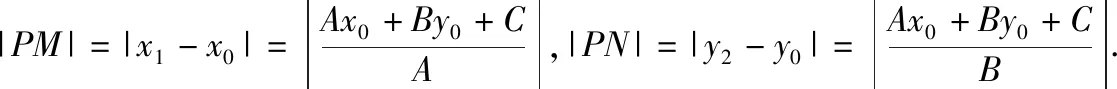
3.“溯源之旅”的生长点

生8：老师，空间点到平面的距离有没有类似公式呢？

师：生8这个“节外生枝”的类比联想问的好！解决了平面内点到线的距离问题，大家自然想到区别于《选修2-1》中向量法求空间点到面的距离的公式.

师：大家能否大胆想想平面方程是什么样？空间点到平面的距离公式是什么样？

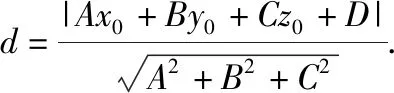
师：很好，这个仅依赖初等方法，根据《必修2》立体几何初步中平面的确定条件、《选修2-1》空间向量等知识可得到证明.

平面内点到线的距离可推广到空间点到面的距离，并有如下基本结论：

(1)在空间直角坐标系中，平面α的一般方程为Ax+By+Cz+D=0(A,B,C,D是不全为0的实数)，则平面α的一个法向量n=(A,B,C).

证明：设平面α内不共线三点为(xi,yi,zi)(i=1,2,3)，则

Ax1+By1+Cz1+D=0， ①

Ax2+By2+Cz2+D=0， ②

Ax3+By3+Cz3+D=0， ③

①-②

得A(x1-x2)+B(y1-y2)+C(z1-z2)=0， ④

①-③

得A(x1-x3)+B(y1-y3)+C(z1-z3)=0， ⑤

由④，⑤可知，(A,B,C)·(x1-x2,y1-y2,z1-z2)=0且(A,B,C)·(x1-x3,y1-y3,z1-z3)=0，

所以n=(A,B,C)是平面α的法向量.

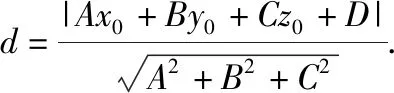
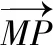
又点P(x,y,z)为平面α内任意一点，所以D=-(Ax+By+Cz),

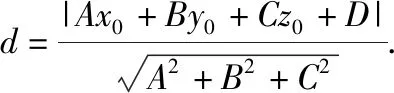
师：空间点到面的距离公式虽然涉及高等数学空间解析几何知识，但我们在合情推理的基础上，用初等方法易于求出平面方程，得到了空间点到平面的距离公式.不难看出，空间点到面的距离公式是平面内点到线距离公式的推广，平面内点到线距离公式是空间点到面距离公式的特例.

4.“溯源之旅”的落脚点

对于空间距离除几何法、向量法、体积法外，公式法不失为一种有效的途径.以下仅就点到平面的距离举例，让学生在自主探索中赏析品味用初等方法解决有高等数学背景问题的乐趣.

例1.在底面边长与高都为2的正四棱锥P-ABCD中，试求底面中心O到侧面的距离.

简析1：如图，以底面中心O为原点建立空间直角坐标系O-xyz，则A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB的方程为Ax+By+Cz+D=0，则将以上3个点的坐标代入计算得A=0,B=-D,2C=-D，

所以平面PAB的方程为2y+z-2=0,

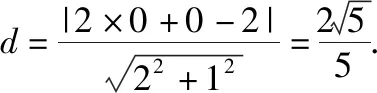
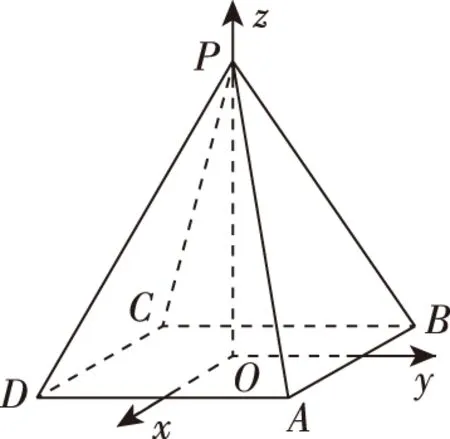
简析2：如图，以底面中心O为原点建立空间直角坐标系O-xyz，A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB内任意一个动点Q(x,y,z),则

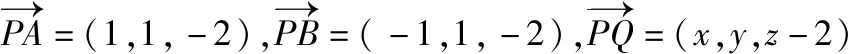
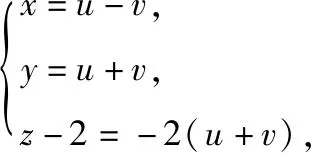
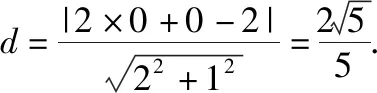
简析3：如图，以底面中心O为原点建立空间直角坐标系O-xyz，A(1,1,0),B(-1,1,0),P(0,0,2),设平面PAB内任意一个动点Q(x,y,z),则

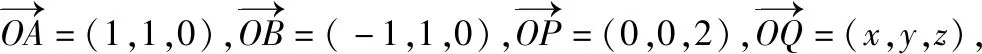
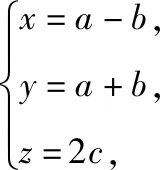
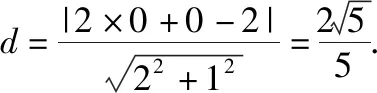
【评析】利用点到平面的距离公式求解，只需先求得平面的方程，然后用待定系数法、共面向量定理、空间向量基本定理等初等方法求平面方程运算都很简便.

例2.如图，在空间直角坐标系中有单位正方体A1B1C1D1-ABCD.

(2)求点C1到平面A1BD的距离.

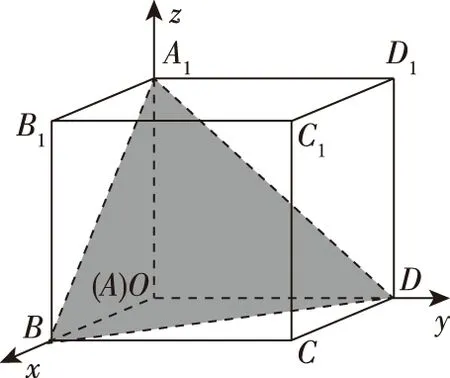
简析：(1)由题意有A1(0,0,1),B(1,0,0),D(0,1,0),C1(1,1,1).设平面A1BD的方程Ax+By+Cz+D=0，则将A1(0,0,1),B(1,0,0),D(0,1,0)三个点的坐标代入计算得A=B=C=-D,

所以平面A1BD的方程为x+y+z-1=0,其法向量n=(1,1,1),

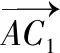
【评析】此解要用待定系数法求得平面A1BD的方程，本题两问可利用结论及距离公式同时解决.

例3.已知点M(-1,1,-2)，平面α过原点，且垂直于向量n=(1,-2,2),求点M到平面α的距离.

简析：由题意可设平面α的方程为Ax+By+Cz=0,则由n⊥平面α,可知

(A,B,C)=λn=(λ,-2λ,2λ)，

所以平面π的方程为x-2y+2z=0,

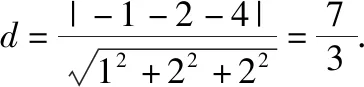
【评析】待定系数法求得平面方程，再利用点到平面的距离公式十分简捷.

二、“溯源之旅”的感悟

距离问题是培养学生直观想象、逻辑推理和数学运算素养的很好载体.中学的距离问题包括点到点的距离、点到线的距离、点到面的距离、线到线的距离、线到面的距离、面到面的距离和球面上两点间的距离七大类型，它们之间可以相互转化，其证明方法既可以用几何法，也可以用向量法.对平面内点到线的距离问题，我们以向量法证明为出发点，追溯其最自然的算法，体验其中的解题思想，并将其推广到空间，相关结论在解决空间距离中发挥了重要作用.经历了“点到直线的距离”的溯源之旅，学生对距离问题的整体认识有了进一步的提高，对其中的数学思想和方法有了深刻的领悟.

荷兰著名数学教育家弗莱登塔尔曾说：“算法意味着巩固,意味着由一个平台向更高点的跳跃.”“溯源之旅”是引导学生对所学知识进行“算法化”的思维跃升过程.因此，要立足提升学生的核心素养，遵循以下原则开展有效的探索活动：

1.发展性原则：通过探本溯源、理清联系、明晰方向、预知未来，进一步明确知识的发生、发展过程.

2.主体性原则：以学生为主体自主探究，引导学生经历探索全程，享受其中的乐趣.

3.完整性原则：选择适宜的时机，保证一定的时间和空间，让学生完整体验知识发生、发展过程，保证学生对知识模块有一个较完整的认识.

溯源之旅中，随着学生自主探究活动的不断展开，新问题不断产生，教学成果往往超乎预设之外.这就需要教师灵活机智地、有针对性地指导、点拨、督促，让学生在自主探索中充分经历知识的发生、发展过程，获得最优化的课堂学习效益.同时，教师对教材的理解和感悟，在很大程度上影响着预设水平和生成质量，因而，教师的功底，也是一种体现教材和课标指向的隐性预设，而这种最大的、全方位的预设成为教师引领溯源之旅的关键所在.