基于误中悟教育方式的课堂实践

安徽

孔子曰：“不愤不启,不悱不发.”问题情境，就是“愤”和“悱”的情境，创设怎样的情境才能让学生在心灵深处真正地理解？为了解决这个问题，以特级教师唐录义为核心的安徽省唐录义名师工作室提出“错亦有情，误中悟道”的课堂创设模式，即创设问题情境，以错题为导向，让学生在错解中悟道，在错解中提升，在错解中升华.这个模式把设置问题情境的过程分为六个步骤：

第一步，考点涉及：指出案例中所涉及的考点、知识内容，以便学生由此在自己的认知结构中提取解决问题相应的知识、方法、经验等信息，为思考提供方向，有的放矢.

第二步，错解呈现：将案例中错误解答的过程完整展示出来.

第三步，错点查找：让学生仔细阅读错解呈现，将其中的错误之处勾画出来.错点查找的方法有顺查法——自题设出发，指向结论，顺藤摸瓜，逐步排查，找出错点.逆查法——从结果入手，倒过来逐步逆推，再看条件是否用完，直到查出错点.分段法——把解题过程分成若干段，根据经验，先查易错段位.

第四步，出错归因：对查出的错点进行剖析，分析致错的深层原因，从双基性失误、策略性失误、心理性失误、逻辑性失误等四个方面进行出错归因分析.

第五步，正解参考：要求学生先做出答案，再阅读案例中提供的正解，将自己的解答与案例提供的解答进行比较.

第六步，反思总结：对于“错”之所以“错”剖析得越深，那么对于“对”之所以“对”也就悟得越透.在前五步纠错过程中获得心得体会，获得思维启迪，获得方法启迪，获得思想启迪的基础上，再进一步进行深刻反思，认真总结，总结发现错误、防范错误、纠正错误、杜绝错误的方法，通过举一反三、触类旁通，悟出正确解决问题的通性通法.

本文就是误中悟教育方式操作总结，包含两个部分：课堂教学的引导和课后训练的设计.

1.课堂教学的引导

1.1概念课：欲擒故纵，让学生在出错后猛醒

在教学“函数的概念”时，笔者发现学生对映射概念认识模糊，笔者在教学时故意插入一个《误中悟》的一个案例：先做好PPT，让学生用10分钟的时间阅读PPT教材，再让同学辨析、讨论，最后师生共同总结.

【例1】设M={a，b，c}，N={-2,0,2},求：

(Ⅰ)从M到N的映射种数；

(Ⅱ)从M到N的映射满足f(a)>f(b)≥f(c),试确定这样的映射f的种数.

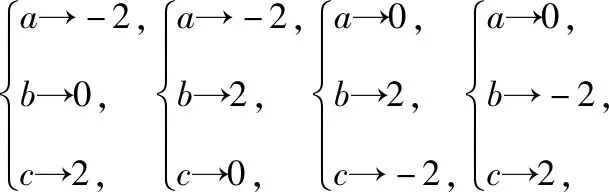
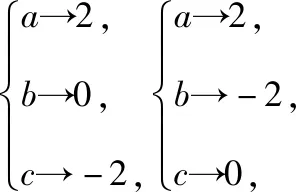
【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)没有找全满足条件的映射个数，关键是对映射概念认识不清，映射的概念要求集合M中元素必须要有象，而且只能有一个象，而集合N中的元素不一定每个都有原象.

【正解参考】(Ⅰ)由于M={a，b，c}，N={-2,0,2}，结合映射的概念，一共有27种映射.

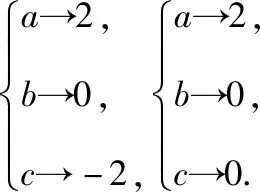
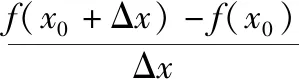
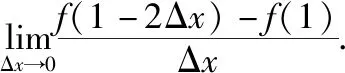
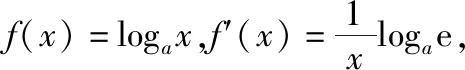
【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)错误的主要原因是对导数的定义理解不清，直接套用公式.

【出错归因】知识性失误，认知结构欠缺，忽视导数的来龙去脉，导致逻辑性失误.

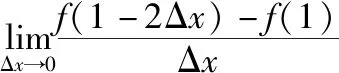
=-2logae.

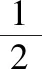
1.2习题课：设疑质疑，让思维在错解中提升

问题是数学的心脏,教会学生解题是中学数学教学的首要任务.同时,由于数学知识严密的逻辑性与高度的概括性,在例、习题中,还隐藏很多没写明的东西.即使最简单的例、习题里,也存在着可发掘的因素,而这些往往并不是学生们所能领会的.因此,在误中悟教学课堂中设计一些有特点的习题,通过错解的方式呈现在学生面前，教师引导学生观察、思考、挖掘错误背后的潜在因素，让学生在错解中理解数学.

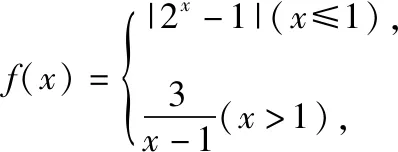
【错解呈现】f(f(a))=|2f(a)-1|，得到f(a)≤1.

当a≤1时，|2a-1|≤1⟺a≤1；

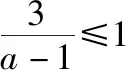
【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)解题者由f(x)的对应法则，f(f(a))=|2f(a)-1|，得到f(a)≤1.这个固然可以，但解题者忽略了f(a)>1时f(f(a))=|2f(a)-1|也可能成立，即f(a)≤1只是原式成立的充分条件，而不是充要条件.

【出错归因】认知结构欠缺，导致逻辑性失误.本题受结构的影响，容易导致认知结构欠缺，从而忽略了问题的另一个方向，导致解题的失误.

( )

( )

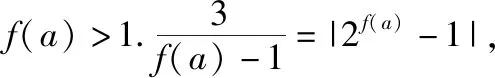
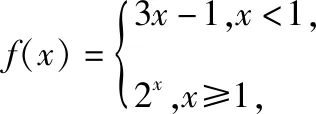
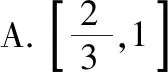
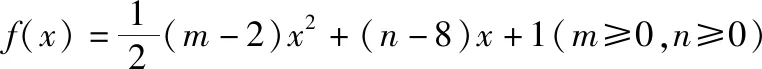
A.16 B.18

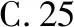
【考点涉及】利用导数求函数的单调性、函数的最值.

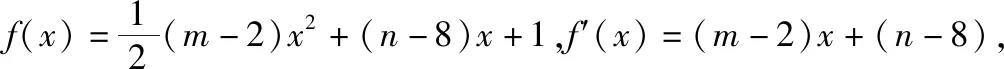
【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)错解误以为在约束条件2m+n-12≤0，m+2n-18≤0，m≥0，n≥0下mn的最大值在可行域的端点处取得，而没有针对问题作具体的分析，草率得出结论.

【出错归因】理解肤浅，思维惯性、僵化，忽略试题中的条件，属于心理性失误.

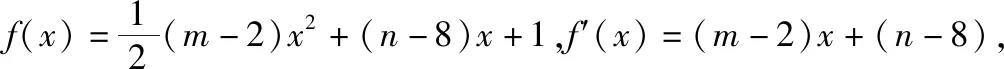
【反思总结】本题的本质是一个线性规划问题：在约束条件下2m+n-12≤0，m+2n-18≤0，m≥0，n≥0，求mn最大值的问题，在习惯性思维的作用下，容易产生在区域的端点处取得最大值的错解.问题的解决取决于认真审题，提炼出线性规划的数学模型，同时具体问题具体分析，不可套用目标函数为一次函数的问题模式.审题是解题的基础，需要认真阅读，仔细推敲，完全明确问题的文字陈述和符号的含义，准确把握问题的条件和结论，必要时还要适当画出图表，列举、提炼出问题的关键，形成题目脉络，纲举目张.

1.3复习课：投石问路，让能力在思辨中提升

数学复习课教学不是简单的重复，它是学生认知的深化和提高，要把旧知识进行整理归纳，将平时相对独立的知识点串成线、连成片、结成网、把复习教学过程组织成学生的再认识过程，从更高的层次，更新的角度进一步掌握，理解已学过的知识和技能，进而提高学生的数学能力.误中悟的复习课的问题设置就是运用错解进行复习，就是围绕着探究目标，促进学生不断达成探究目标，通过一系列的相互联系的错解引发学生有层次的思考，拓展学生思维的深度和广度.本文以高一数学函数的复习为例设置几个案例供大家参考.

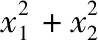
【考点涉及】二次函数在区间上的最值.

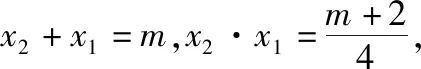
【出错归因】心理性失误：理解不透，忽略隐含条件.一元二次方程韦达定理的应用是在判别式Δ≥0的前提之下建立的，解题时不可疏忽，不可漏掉这个关键条件.

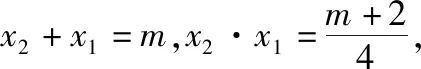
因为方程4x2-4mx+m+2=0有两根，故Δ=(-4m)2-

4·4(m+2)≥0，得m≥2或m≤-1，

【反思总结】一元二次方程根的判别式可以用来判定方程根的情况，应用极其广泛.学生在应用根与系数的关系解有关一元二次方程的数学问题时，常常忽视判别式的作用，以致给解题带来不必要的失误.

【考点涉及】函数图象、函数的值域、数形结合.

【错点查找】(请仔细阅读上面的“错解呈现”，并将其中错误之处勾画出来)上述解法中，只注意到函数值的对应，而忽略了函数图象的变化趋势.

【出错归因】未着眼问题本质，本题的本质是函数单调性和奇偶性、值域的结合；解题角度不当，仅从对应关系入手，而不是从图象中看清试题的本质.

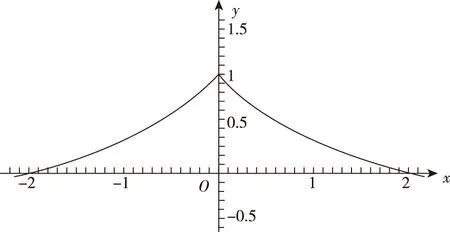
根据图象可得到满足题意的整数对(a,b)有：(-2,2),(-2,1),(-2,0),(-1,2),(0,2)，共五对.

【反思总结】我国著名数学家华罗庚曾说过：“数缺形时少直观,形少数时难入微；数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.本题中，如果没有函数图象，则整个解题过程就是雾里看花，让人摸不着头脑.

2.课后训练的设计

误中悟理论认为：课后训练是有目的、有指导、有组织的学习活动，是学生掌握知识、形成技能、发展智力的基本途径.因而，提高练习的效率，是提高教学质量的重要保证，高效练习的目的是巩固和加强新知，是新授课的补充和延续.因此误中悟的课后训练是对传统的课后练习的一种提升和加强，它的设计具有以下特点：

(1)多一些问题解决，少一些理论操作.新课程标准指出：练习的设计要围绕着问题解决而设计，而且问题解决也成为考试考查的内容之一.误中悟的课后训练与常规的练习的主要区别之一是：练习着重寻求答案，而误中悟的课后设计重点在于解决问题的过程，重点是如何突破认知上的瓶颈.

【例7】函数f(x)=x3+ax2+bx+a2在x=1处有极值10，则

( )

A.a=-3,b=3

B.a=4,b=-11

C.a=-4,b=11

D.a=-3,b=3或a=4,b=-11

【错解呈现】函数f(x)=x3+ax2+bx+a2在x=1处有极值10，则f′(x)=3x2+2ax+b,f′(1)=3+2a+b=0,f(1)=1+a+b+a2=10，解得a=-3,b=3或a=4,b=-11，故选D.

【正解参考】B.

(2)课后训练要遵循学生的认知规律.训练要根据知识的结构特征和学生的认知规律及新课程标准的要求精心设计练习，做到由浅到深，有层次，有梯度，环环相扣.通过多层次的训练，使学生在简单运用、综合运用、解决问题、扩展创新的过程中，理解和掌握知识，能力得到发展，同时也要照顾到不同层次的学生的学习水平.

【例8】如图是导函数y=f′(x)的图象，试找出函数y=f(x)的单调区间、极值点，并指出哪些是极大值点，哪些是极小值点.

【错解呈现】如图易知，函数y=f(x)的单调递增区间为(a,x1),(x3,x5),(x6,b)，单调递减区间为(x1,x3),(x5,x6)，极值点分别为x1,x3,x5,x6.

【正解参考】函数f(x)的单调增区间为(a,x2),(x4,b)单调减区间为(x2,x4)；极大值点为x2极小值点为x4.

(3)课后训练要有针对性.训练的针对性是指练习要有的放矢，对学生易错的地方设计课后训练，以便帮助学生掌握知识，避免盲目性.

在高三理科一次测验中，笔者选用了2014年高考天津卷理科数学第21题，把它的第一问改编为一道选择题：

已知函数h(x)=x-aex有两个零点，则a的取值范围是

( )

A.(0,e-1) B.(e-1,+∞)

C.(-∞,e-1) D.(0,+∞)

没想到，这道题的得分率很低，更让人百思不得其解的是，有近一半的同学选了C答案.

在讲解这个题目时，笔者表达了对同学们答题情况的困惑.这时，一个成绩中等的同学举手了，他说为什么他用导数的方法，求得答案应该是C呢，其解法如下：

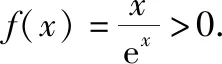
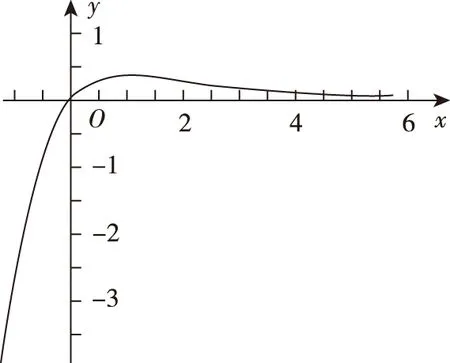
这是用导数方法解题的一个常见错误，能不能正确地作出函数图象是解题的关键，学生在作图的时候只是关注了函数的单调性，而没有关注函数的变化趋势.

面对大批学生犯的同样错误，笔者心想，仅就一个例子，不足以纠正学生错误的行为，笔者课后就此问题设计了几个案例.

作业：1.用分离变量的方法讨论关于x的方程x2-alnx=0(a∈R)的解的个数.

2.讨论关于x的方程a=xlnx(a∈R)的解的个数，并说明理由.