核心素养导向下全国理科卷“函数与导数”试题研究与备考

广东

1 近六年全国理科卷高考试题考查情况的统计与分析

1.1近六年高考全国卷理科数学试题分布

1.1.1近六年高考全国卷Ⅰ理科数学试题分布

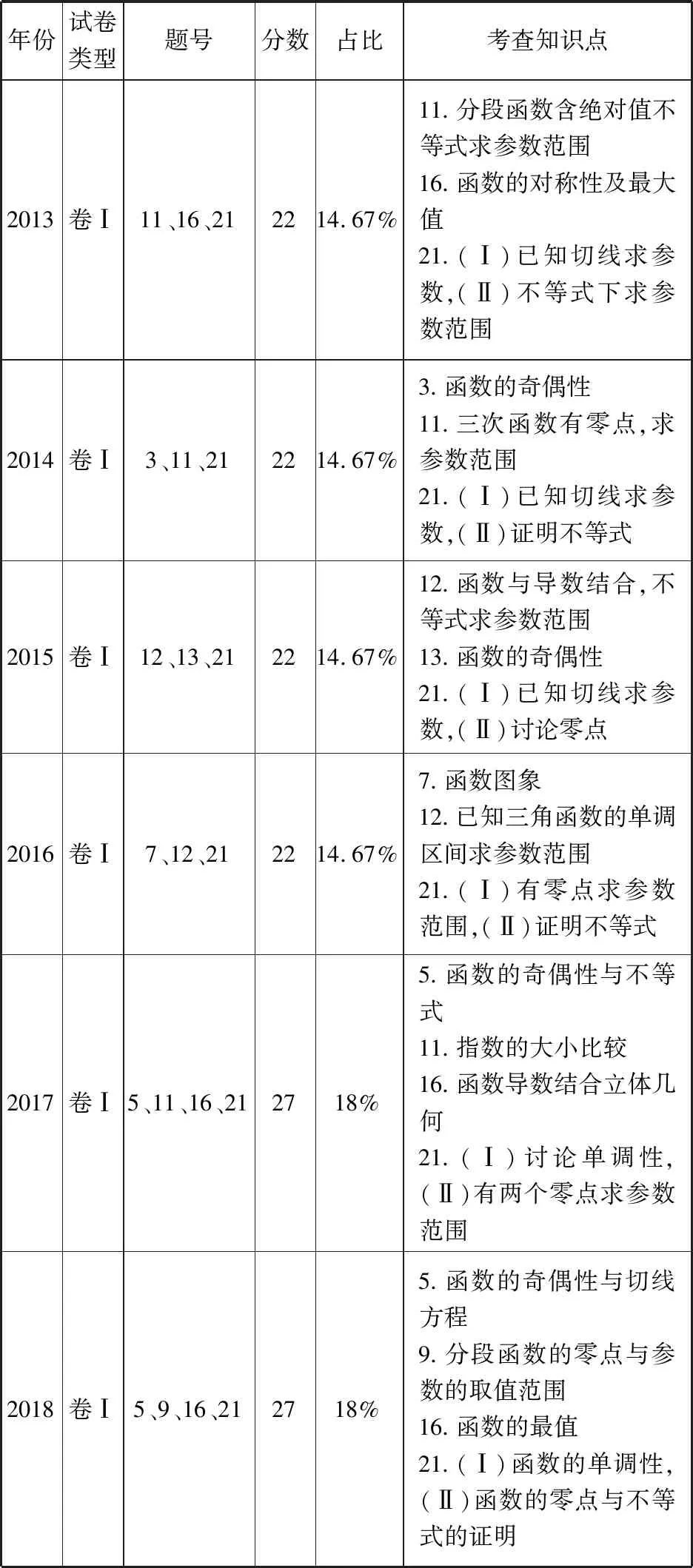
年份试卷类型题号分数占比考查知识点2013卷Ⅰ11、16、212214.67%11.分段函数含绝对值不等式求参数范围16.函数的对称性及最大值21.(Ⅰ)已知切线求参数,(Ⅱ)不等式下求参数范围2014卷Ⅰ3、11、212214.67%3.函数的奇偶性11.三次函数有零点,求参数范围21.(Ⅰ)已知切线求参数,(Ⅱ)证明不等式2015卷Ⅰ12、13、212214.67%12.函数与导数结合,不等式求参数范围13.函数的奇偶性21.(Ⅰ)已知切线求参数,(Ⅱ)讨论零点2016卷Ⅰ7、12、212214.67%7.函数图象12.已知三角函数的单调区间求参数范围21.(Ⅰ)有零点求参数范围,(Ⅱ)证明不等式2017卷Ⅰ5、11、16、212718%5.函数的奇偶性与不等式11.指数的大小比较16.函数导数结合立体几何21.(Ⅰ)讨论单调性,(Ⅱ)有两个零点求参数范围2018卷Ⅰ5、9、16、212718%5.函数的奇偶性与切线方程9.分段函数的零点与参数的取值范围16.函数的最值21.(Ⅰ)函数的单调性,(Ⅱ)函数的零点与不等式的证明

1.1.2近六年高考全国卷Ⅱ理科数学试题分布

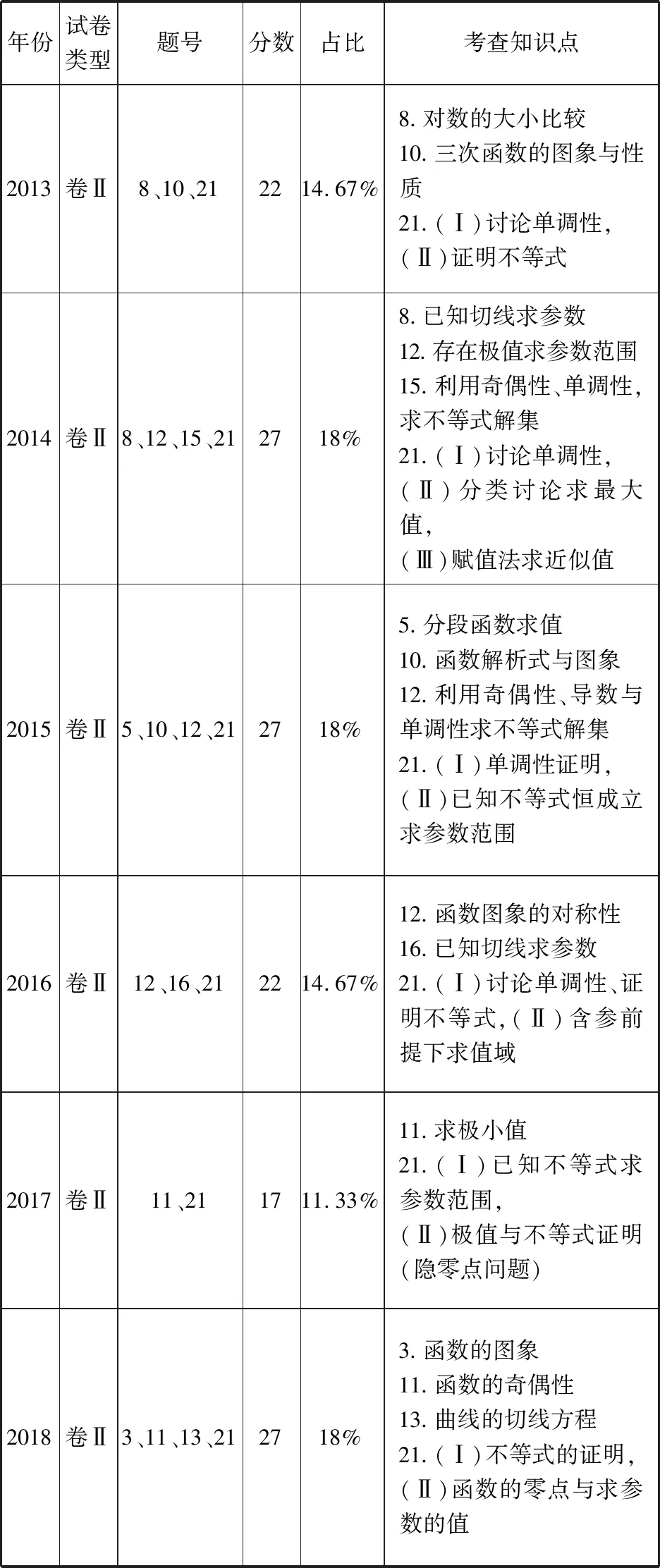
年份试卷类型题号分数占比考查知识点2013卷Ⅱ8、10、212214.67%8.对数的大小比较10.三次函数的图象与性质21.(Ⅰ)讨论单调性,(Ⅱ)证明不等式2014卷Ⅱ8、12、15、212718%8.已知切线求参数12.存在极值求参数范围15.利用奇偶性、单调性,求不等式解集21.(Ⅰ)讨论单调性,(Ⅱ)分类讨论求最大值,(Ⅲ)赋值法求近似值2015卷Ⅱ5、10、12、212718%5.分段函数求值10.函数解析式与图象12.利用奇偶性、导数与单调性求不等式解集21.(Ⅰ)单调性证明,(Ⅱ)已知不等式恒成立求参数范围2016卷Ⅱ12、16、212214.67%12.函数图象的对称性16.已知切线求参数21.(Ⅰ)讨论单调性、证明不等式,(Ⅱ)含参前提下求值域2017卷Ⅱ11、211711.33%11.求极小值21.(Ⅰ)已知不等式求参数范围,(Ⅱ)极值与不等式证明(隐零点问题)2018卷Ⅱ3、11、13、212718%3.函数的图象11.函数的奇偶性13.曲线的切线方程21.(Ⅰ)不等式的证明,(Ⅱ)函数的零点与求参数的值

1.1.3近三年高考全国卷Ⅲ理科数学试题分布

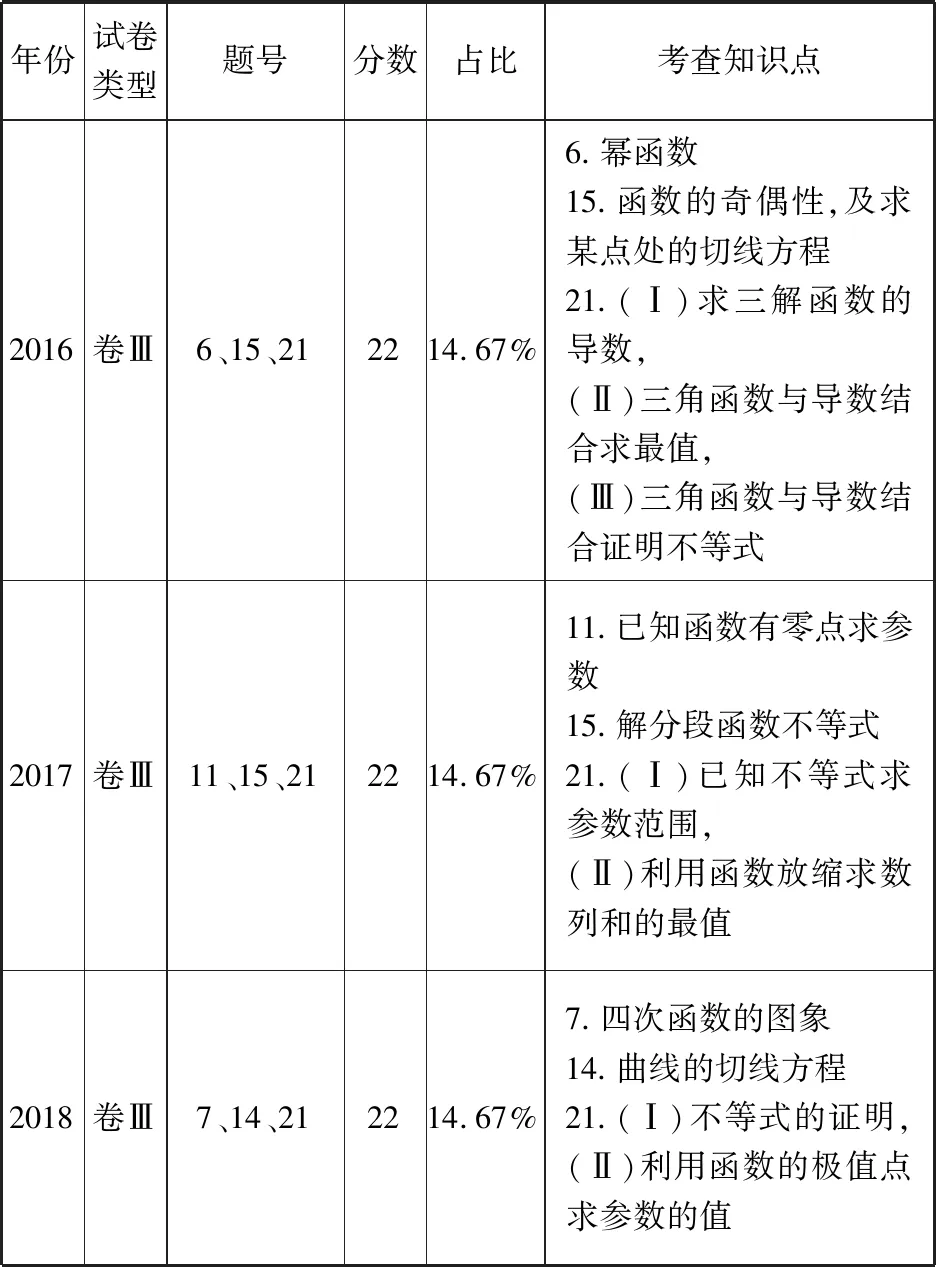
年份试卷类型题号分数占比考查知识点2016卷Ⅲ6、15、212214.67%6.幂函数15.函数的奇偶性,及求某点处的切线方程21.(Ⅰ)求三解函数的导数,(Ⅱ)三角函数与导数结合求最值,(Ⅲ)三角函数与导数结合证明不等式2017卷Ⅲ11、15、212214.67%11.已知函数有零点求参数15.解分段函数不等式21.(Ⅰ)已知不等式求参数范围,(Ⅱ)利用函数放缩求数列和的最值2018卷Ⅲ7、14、212214.67%7.四次函数的图象14.曲线的切线方程21.(Ⅰ)不等式的证明,(Ⅱ)利用函数的极值点求参数的值

1.2“函数与导数”的命题特点

1.2.1考查形式和分值占比稳定，形式略有创新

卷Ⅰ往年一般是两道小题和一道解答题，简称两小一大，共22分，2017、2018年是三小一大，共27分，并且注重在知识的交汇处命题，如2018年卷Ⅰ第16题考查导数在三角函数中的应用，2017年卷Ⅰ第16题综合考查立体几何与函数及导数，体现了试题在代数与几何结合中的应用；卷Ⅱ稍有波动，2017年是一小一大，分值17分，2013、2016年是两小一大，分值22分，2014、2015、2018年有所增加，三小一大，分值27分；从2016年开始有全国卷Ⅲ，试题基本稳定，两小一大，分值22分.总体上看“函数与导数”高考命题风格稳定与创新共存，分值占比稳定在11.33%—18%，选择填空题有易有难，解答题固定在压轴题，大多都是两问，卷Ⅰ、卷Ⅱ解答题难度有所降低，但卷Ⅲ难度很大，说明总趋势有所降低，但依然存在许多不稳定因素.

1.2.2考查知识点全面

近六年来高考全国卷理科数学试题对“函数与导数”内容考查知识点比较全面，重点考查学生对基本概念、基本公式、基本定理的理解和应用，兼顾考查数学能力、数学思想方法以及数学核心素养.小题主要考查函数图象性质、导数的几何意义等，包括函数图象识别、函数的单调性、对称性、奇偶性以及周期性、切线问题，其中指数和对数函数的性质及其运算有加强的趋势，比如2017年理科卷Ⅰ第11题，设x,y,z为正数，且2x=3y=5z，比较2x,3y,5z的大小，重点考查了指数与对数的转化和对数的运算，意在考查考生推理论证能力以及运算求解能力.解答题主要考查函数与导数的应用，注重细化分类、讨论单调性，结合图形讨论零点与最值，注重证明不等式的技巧与方法.

1.2.3凸显能力立意，承载压轴使命

“函数与导数”多以中档题和难题为主，试题层次分明，区分度好，解法灵活多变，充分体现了试题设计的基础性、综合性、创新性以及应用性，较好地考查了不同层次学生的分析问题和解决问题的能力，其中解答题为试卷压轴题，服务高效选拔，突出对学生推理论证能力、抽象概括、运算求解能力以及逻辑推理、数学抽象、数学运算等学科核心素养的考查.

2 “函数与导数”命题角度分析

研究历年高考真题，力求真题引领教学方向，通过对近六年高考全国理科卷“函数与导数”命题特点分析，“函数与导数”试题主要考查了以下几种类型的问题.

2.1有关“函数的图象和性质”试题

2.1.1判断函数的单调性、奇偶性、对称性、识别函数的图象

例1.(2014·全国卷Ⅰ理·3)设函数f(x),g(x)的定义域都为R，且f(x)是奇函数，g(x)是偶函数，则下列结论中正确的是

( )

A.f(x)g(x)是偶函数 B.|f(x)|g(x)是奇函数

C.f(x)|g(x)|是奇函数 D.|f(x)g(x)|是奇函数

评析:本题主要考查函数的奇偶性

答案：C.

( )

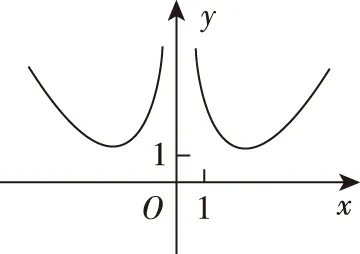
A

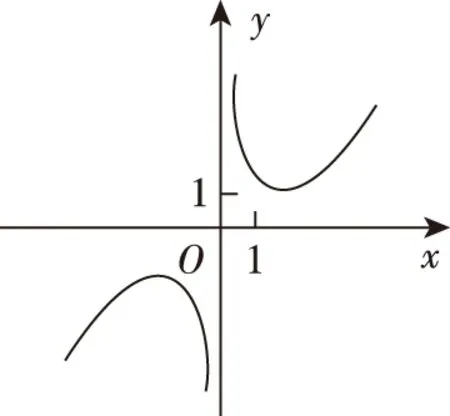
B

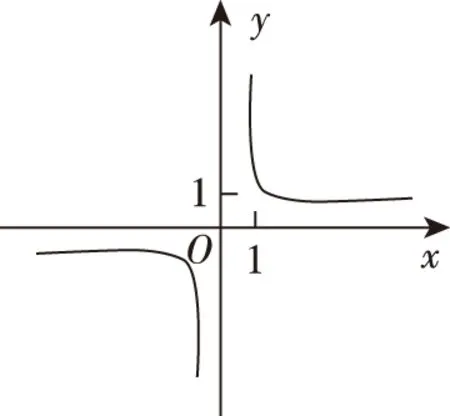
C

D

评析:本题是根据函数的解析式判断函数的图象，也是近几年高考的常考题型，偶尔也需要先根据题目条件建立函数模型，再来判断函数的解析式或者研究函数的图象性质，更加深刻地考查学生的数学建模、数学抽象、逻辑推理、直观想象等学科素养.例如2015年理科卷Ⅱ第10题、2017年理科卷Ⅰ第16题.

答案：B

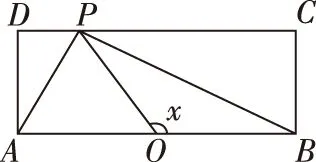
例3.(2015·全国卷Ⅱ理·10)如图，长方形ABCD的边AB=2，BC=1，O是AB的中点.点P沿着边BC，CD与DA运动，记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x)，则y=f(x)的图象大致为

( )

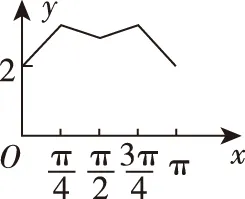
A

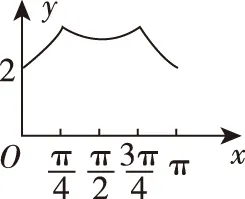
B

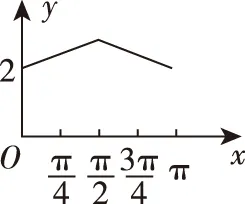
C

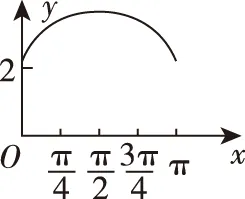
D

答案：B.

例4.(2017·全国卷Ⅰ理·16)如图，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O.D，E，F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D，E，F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为________.

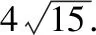
2.1.2求函数的函数值或者参数

例5.(2018·全国卷Ⅱ理·11)已知f(x)是定义域为(-∞,+∞)的奇函数，满足f(1-x)=f(1+x).若f(1)=2，则f(1)+f(2)+f(3)+…+f(50)=

( )

A.-50 B.0

C.2 D.50

评析：本题主要考查抽象函数的奇偶性、周期性，考查学生数形结合能力以及分析问题、解决问题的能力，考查逻辑推理、数学运算核心素养.

答案：C.

例6.(2013·全国卷Ⅰ理·16)若函数f(x)=(1-x2)(x2+ax+b)的图象关于直线x=-2对称，则f(x)的最大值为________.

评析：本题是根据函数的对称性求函数解析式的参数，进而求函数的最大值.

答案：16.

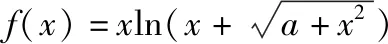
评析：本题是根据函数的奇偶性求函数解析式中的参数.

答案：1.

2.2运用导数研究函数的性质

“函数与导数”是高中数学的重要内容，研究函数离不开导数这个工具，利用导数研究函数的性质是高考热点问题，包括研究函数单调性、极值、最值、切线和函数的零点等问题，特别是有关函数零点的试题更是备受全国卷青睐，运用导数研究函数的性质往往需要画出函数图象的草图，利用数形结合的思想来分析解决问题.

例8.(2018·全国卷Ⅰ理·5)设函数f(x)=x3+(a-1)x2+ax.若f(x)为奇函数，则曲线y=f(x)在点(0,0)处的切线方程为

( )

A.y=-2xB.y=-x

C.y=2xD.y=x

评析：此题比较简单，考查函数的性质与利用导数工具求切线方程，充分体现了命题者考基础、考概念的基本思路.本题主要考查奇函数的定义、导数的几何意义，考查运算求解能力，考查的核心素养是数学运算.

答案：D.

例9.(2018·全国卷Ⅱ理·13)曲线y=2ln(x+1)在点(0,0)处的切线方程为________.

评析：主要考查导数的几何意义，考查的核心素养是数学运算.

答案：y=2x.

例10.(2018·全国卷Ⅲ理·14)曲线y=(ax+1)ex在点(0,1)处的切线的斜率为-2，则a=________.

评析：本题主要考查导数的几何意义，考查考生分析问题、解决问题的能力，考查的核心素养是数学运算.

答案：-3.

例11.(2016·全国卷Ⅱ理·16)若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln(x+1)的切线，则b=________.

评析：本题考查导数在研究函数图象(曲线)的切线中的应用及方程思想，对考生的基本运算能力有较高的要求.

答案：1-ln2.

例12.(2018·全国卷Ⅰ理·16)已知函数f(x)=2sinx+sin2x，则f(x)的最小值是________.

评析：本题主要考查三角函数的最值，导数的应用，考查考生的化归与转化能力、运算求解能力，考查的核心素养是数学运算.

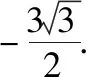
(Ⅰ)当a为何值时，x轴为曲线y=f(x)的切线；

(Ⅱ)用min{m,n}表示m,n中的最小值，设函数h(x)=min{f(x),g(x)}(x>0)，讨论h(x)零点的个数.

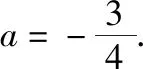
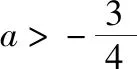
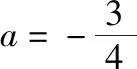
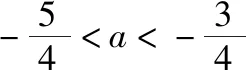
例14.(2016·全国卷Ⅰ理·21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围；

(Ⅱ)设x1,x2是f(x)的两个零点，证明：x1+x2<2.

答案：(Ⅰ)a的取值范围为(0，+∞).(Ⅱ)证明略.

例15.(2018·全国卷Ⅱ理·21)已知函数f(x)=ex-ax2.

(Ⅰ)若a=1，证明：当x≥0时，f(x)≥1；

(Ⅱ)若f(x)在(0,+∞)只有一个零点，求a.

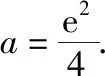
例16.(2015·全国卷Ⅰ理·12)设函数f(x)=ex(2x-1)-ax+a,其中a<1，若存在唯一的整数x0使得f(x0)<0，则a的取值范围是

( )

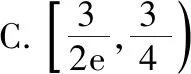
答案：D.

2.3运用导数研究不等式问题

“函数与导数”解答题作为压轴题，第二问常常出现不等式证明问题，不等式恒成立问题以及函数零点问题，解决此类问题的通法一般是通过合理转化与恰当构造新函数，然后利用导数去解决问题.

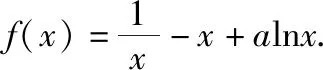
(Ⅰ)讨论f(x)的单调性；

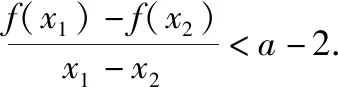
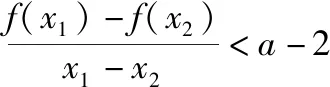
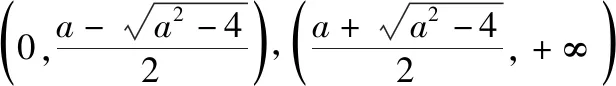
例18.(2018·全国卷Ⅱ理·21)已知函数f(x)=ex-ax2.

(Ⅰ)若a=1，证明：当x≥0时，f(x)≥1；

(Ⅱ)若f(x)在(0,+∞)只有一个零点，求a.

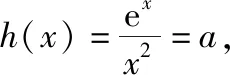
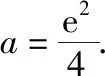
例19.(2013·全国卷Ⅱ理·21)已知函数f(x)=ex-ln(x+m).

(Ⅰ)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；

(Ⅱ)当m≤2时，证明：f(x)>0.

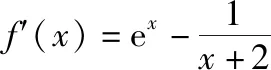
本题第二问不等式证明中涉及的隐零点(导函数的零点存在但不易求出)是近几年备考全国卷的热点问题，在各地模拟试题中屡见不鲜，解决隐零点问题通常采用对导函数零点“设而不求”“整体代换”的技巧来研究.

答案：(Ⅰ)m=1,f(x)在(-1，0)上单调递减，在(0，+∞)上单调递增.(Ⅱ)证明略.

3 备考建议

3.1紧扣教材，夯实基础

在复习备考中，要依靠考纲，紧扣教材，做到源于课本、高于课本，夯实数学基础知识，引导学生构建“函数与导数”的知识网络，重视数学基本思想的形成，注重通性通法的积累和熟练应用.第一，以形助数，抓住函数的单调性、奇偶性、对称性、周期性等函数的基本性质；第二，对于各类切线问题要重点训练，含参函数分类讨论单调性要做到熟练与精通；第三，注意基本函数的各种组合模型，让学生熟悉以组合为载体考查单调性，极值、最值、零点问题，特别是ex与lnx两个初等函数与一次函数、二次函数、分式函数相结合.(注意：既是零点又是极值点这类题目的分类讨论，特别是恒成立求参数的取值范围时这一方法经常采用，比如2010年湖北理科卷第21题、2012年天津理科卷第20题、2015年北京理科卷第18题、2015年山东理科卷第21题，2016年江苏第19题)

3.2因材施教,实施分层教学策略

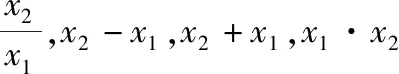
3.3培养“创新意识”，强化“探究能力”