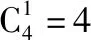2019年高考数学命题新特点展望
——“六核四性一化”之我见
浙江
早在十五年前,在“数学通讯”上就提出高考数学命题的“六化”趋势,即实际问题数学化、高等数学初等化、学科问题综合化、问题内容创新化、形式结构开放化和自主探究课题化.如今,2019年高考数学大纲明确提出来的“六核四性一化”与“六化”属性相同,观点一致,2019年高考数学大纲中明确将数学学科核心素养渗透到高考数学命题之中,“在能力要求内涵方面,增加了基础性、综合性、应用性、创新性的要求,增加了数学文化的要求.同时对能力要求进行了加细说明,使能力要求更加明确具体”,提出了从数学思想方法、数学能力、数学的科学与人文价值三个方面考查学生的数学学习情况,体现了知识与能力并重,科学与人文兼顾的精神,有利于引导中学数学教学更加注重思想性、文化性、灵活性,有利于实现全面提升和培养学生综合的数学素养,高考与新课程改革的同步联系,大纲修改契合课程标准的修订方向,2019年以前的各地高考数学命题已经有所展示,2019年高考数学试题将把六大核心数学素养“数学抽象,逻辑推理,数学建模,直观想象,运算能力,数据分析”渗透于“基础性,综合性,应用性,创新性,数学文化”之中,使之更加突出.
1.基础性为数学理解之前提
数学复习突出对数学概念、基本运算、基本性质的整体理解、掌握与运用,力求全面而有效,仅仅一知半解,死套公式可能就不行了,特别是教与学中的“题型+方法”的风格要做改变,基础性一定体现在对核心知识点的理解与掌握,对数学基本方法与推理过程完整全面的理解,高考数学的基础性还体现在“数学抽象”“逻辑推理”“运算能力”等核心素养上.
比如,集合元素个数的计算card(A∪B)=card(A)+card(B)-card(A∩B)是一个非常基础的数学知识点,下列问题将其恰到好处地设计其中,
例1.(原创)A6={(x1,x2,x3)|xi=1,2,3,4,5,6,i=1,2,3且6|x1x2x3}(“|”表示整除),从集合A6中随机抽取一个元素(x1,x2,x3),使得12|(x1+x2+x3)的概率为
( )
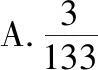
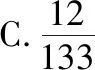
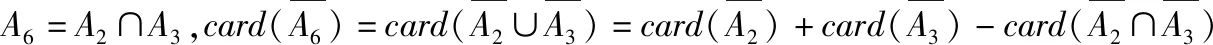
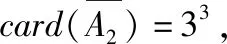
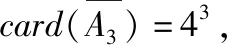
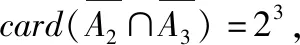

满足“12|(x1+x2+x3)”的元素只有(1,5,6)(2,4,6)(3,4,5)三类,
解读:计算card(A6)是本题最核心、最基础的部分,学生可能会用分类讨论方式解决card(A6)的计算问题,但困难重重,失误多多,然而利用集合元素个数的计算公式却如此简洁恰当!值得一提的是集合语言的抽象性也是学生思维的障碍点,将A6用另一种语言描述为“集合A6是由一枚骰子连续投三次出现的点数,其积被6整除而组成的元素全体.”
2.综合性为有效复习之抓手
高考数学命题突出知识交汇处的融合,体现数学知识的内在联系,在过去十多年的高考数学命题中,这一方面已展现得十分得体,综合性不仅体现在命题本身的内在需要,而且也体现在检测学生面对综合性问题的分析思考能力,化综合为单一,化综合为具体,化综合为层层递进.新课程高考数学题将数学知识融合或交汇变为一种趋势.比如,2013年四川题将程序框图与抽样的频率分布图融合,把数据收集方法与数学处理方法交织在一起;随机变量的分布与统计和程序设计融合,反映统计工作者的实际工作的全过程;湖北题将正态分布与线性规划融合;江西题将概率与向量交汇等,以此检测考生应用概率统计知识解决实际问题的能力,“数学建模”与“数据分析”核心素养成为概率统计命题的重中之重.
例2.(2013·湖北卷理·20)假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量,记一天中从甲地去乙地的旅客人数不超过900的概率为p0.
(Ⅰ)求p0的值;
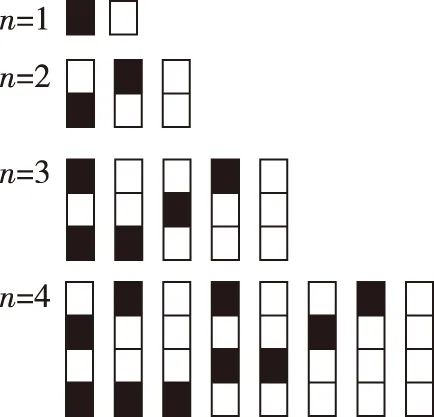
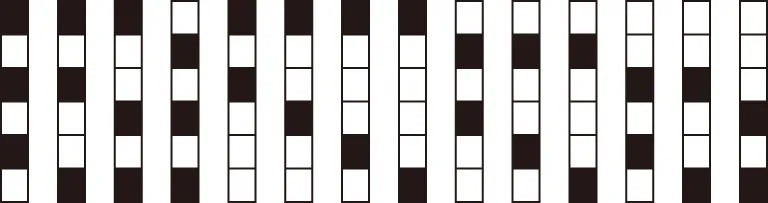
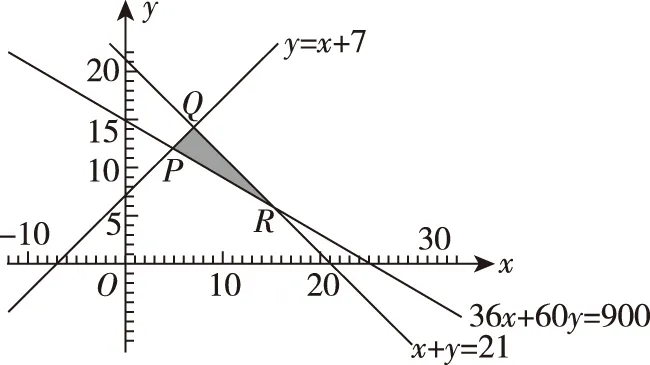
(参考数据:若X~N(μ,σ2),有P(μ-σ (Ⅱ)某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次,A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆? P(η≤2)=P(-2≤η≤2)+P(η≤-2)=P(-2≤η≤2)+P(η≥2)=P(-2≤η≤2)+(1-P(η≤2)), 2P(η≤2)=1+P(-2≤η≤2)=1.954 4,p0=P(η≤2)=0.977 2. 解法二:由于随机变量X服从正态分布N(800,502),故有μ=800,σ=50,P(700 (Ⅱ)设配备A型车,B型车数量分别为x,y辆,则相应的营运成本为1 600x+2 400y,依题意,x,y还需满足x+y≤21,y≤x+7,P(X≤36x+60y)≥p0, 由(Ⅰ)知,p0=(X≤900),故P(X≤36x+60y)≥p0等价于36x+60y≥900, 且使目标函数z=1 600x+2 400y达到最小的x,y. 作可行域如图中阴影部分(含边界)所示,可行域的三个顶点分别为P(5,12),Q(7,14),R(15,6), 解读:将概率统计知识与线性规划知识自然融合,避开现有应用题的模式,保持适度创新,规避题型套路,强调通性通法,淡化特殊技巧,并不等于一味地迎合中学教学盛行的题型套路.试题采用“适度创新”和“规避模式”的做法,做到“新、变”但不怪,“新、变”而不难.题面形式:用概率p0将正态分布与线性规划问题有机结合在一起. 数学复习中渗透且突出数学建模意识、解决实际问题的能力与素养的检测,自1995年数学应用题进入高考数学试卷以来,数学应用问题的教学与高考数学命题所占份额各地不尽相同,差异较大,然而,数学命题的应用性不仅体现数学在实际问题中的应用,而且也强调数学内部的知识与知识间的应用,数学的三大语言(自然语言、符号语言、图形语言)的综合应用. ( ) 解读:此题的创作突出自然语言、符号语言、图形语言的融合,体现解析几何、立体几何和解三角形的综合,通径概念在教材上已介绍,将圆锥曲线与空间图形有机结合,把三大语言应用于圆锥曲线基本量与空间图形中度量关系的融合交汇上,此例可以继续挖掘,变换不同的三个点F1,A,B或顶点,A,B或中心,A,B等,曲线可由椭圆变成双曲线或抛物线或其他曲线等,可以产生不同的数量关系. 高考数学命题的最大特点在于它的创新性,数学复习时突出设问角度的进一步创新,设问条件的进一步抽象,呈现出命题与研究性学习方法相融合,命题与数学模型的进一步深化相融合,命题与探究性相融合,命题与时代气息相融合等等. 例4.(原创)在古运河上建有许多形状相同的抛物线型拱桥An(n=0,1,2,…),经测量知,相邻两座桥之间的距离an近似满足an=800+150n(n=1,2,3,…).这些拱桥当水面距拱顶5米时,桥洞水面宽为8米,每年汛期,船公都要考虑拱桥的通行问题.一只宽4米,装有防汛器材的船,露出水面部分的高为0.75米. (Ⅰ)要使该船能顺利通过拱桥,试问水面距拱顶的高度至少几米? (Ⅱ)已知河水每小时上涨0.15米,船在静水中的速度为0.4米/秒,水流速度为15米/分,若船从A0桥起锚顺水航行时,河水开始上涨,试问船将在哪一座桥可能受阻? (Ⅲ)若船通过An-1桥后,An桥可能受阻,你会采取什么措施使该船顺利通过此桥?(船长、桥宽、采取措施所用时间忽略不计) (Ⅲ)当船通过An-1桥后,发现船可能在An桥受阻,船公可以立即采取加快船速的方法;或者给船加载使船体下沉(不超过0.75米)等方法,使船顺利通过An桥,此答案不唯一. 解读:浙江许多城市都是水乡、桥乡,由景生题,编制上述问题.问题以综合分析能力立意,将数列、抛物线、方程等知识融为一体,主要测试学生的阅读理解能力、综合应用能力及数学思维能力,包括思维的严密性:第(Ⅰ)问容易漏掉0.75,第(Ⅱ)问容易错将n定为19;思维的发散性:只要将第(Ⅱ)问中的“顺水”删除,学生需要考虑两种情形:顺水和逆水;思维的创造性:第(Ⅲ)问既测试学生的综合素质,又为学生的创新思维提供了空间,使问题具有开放性和广泛性. 我国进入新时代,在基础教育中突出“以德育人”,如何将数学的教育功能渗透于高考数学之中是数学命题专家一直在探索的课题,为此,高考数学复习突出提炼数学问题的数学思想,突出数学传统文化的渗透,王梓坤先生曾说:“数学文化具有比数学知识体系更为丰富和深邃的文化内涵,数学文化是对数学知识、技能、能力和素养等概念的高度概括.”可见,数学文化和传统的命题素材并不冲突,从时间跨度来看,从古代到现代,只要是精华,在数学命题时就有继承的必要,毫无疑问,在数学复习中加5%的数学文化传承的试题,给予学生数学概念本质的传授、数学解题方法的传授是必要的,但在介绍数学概念的同时,渗透数学文化,渗透中华数学文化的经典也是必要的. 例5.(2011·湖北卷理·15)给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如下图所示: 由此推断,当n=6时,黑色正方形互不相邻的着色方案共有________种,至少有两个黑色正方形相邻的着色方案共有________种.(结果用数值表示) 解析:首先将题读懂.为使黑色正方形互不相邻: n=1时,每列只1个小方格,仅有黑,白各一个小方格,共2种形式; n=2时,每列2个小方格,至多只能将1个方格着黑,故有白,黑;黑,白;白,白3种形式; n=3时,每列3个小方格,有2格着黑的1种,一格着黑的3种,全白的1种,共5种形式; n=4时,每列4个小方格,有2格着黑的3种,1格着黑的4种,全白的1种,共计3+4+1=8种形式; 以上共计4+10+6+1=21种形式.此外,不受限制的着色方案,每个小方块都有黑,白两种着色方案,所以6个小方块共有26=64种着色方案.如前所述,其中黑色正方形互不相邻的着色方案有21种,故至少有两个黑色正方形相邻的着色方案共有64-21=43种. 观察研究当n=1,2,3,4,…时符合题意的着色方案,其数量依次为2,3,5,8,13,21,….这是我们多么熟悉的黄金数列,也就是n≥2时,每后一项等于其前2项之和.如果考生们运用此方案,就能够在几秒钟内找到正确答案. 解读:该题一方面可以看成是涂色问题,运用排列组合相关知识可以解答;另一方面可以找出规律,发现这其实是一个斐波那契数列问题,运用数列相关知识解决,所以此题是一道典型的具有数学文化背景的高考试题.其创新之处就是在四色问题和斐波那契数列的基础上,以图形为依托,表面上是一道普通的涂色问题,考查的是排列组合知识;实质上通过创设一个斐波那契数列的问题情境,考查学生的归纳猜想能力和合情推理意识.从命题的角度讲,该题基于数学文化,属于经典问题改造,这种改造,主要是形式上的,但是这种改造仍使很多考生不适应,究其原因,学生或者是缺乏数学文化的素养,或者是不能透过表面现象去洞察问题的实质.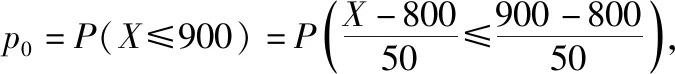
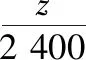
3.应用性为应用能力之体验
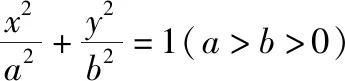
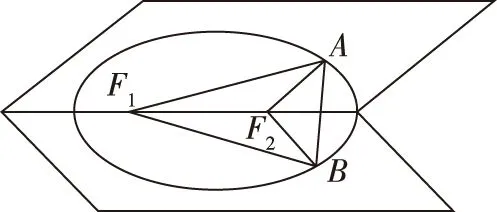
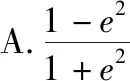

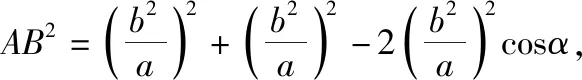

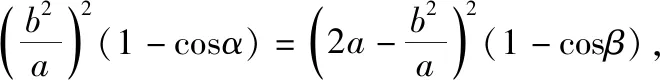
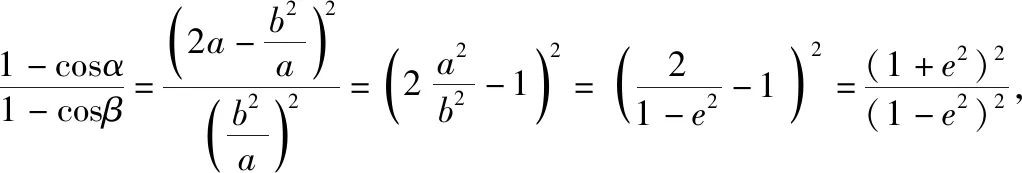
4.创新性为拓展思维之巅峰
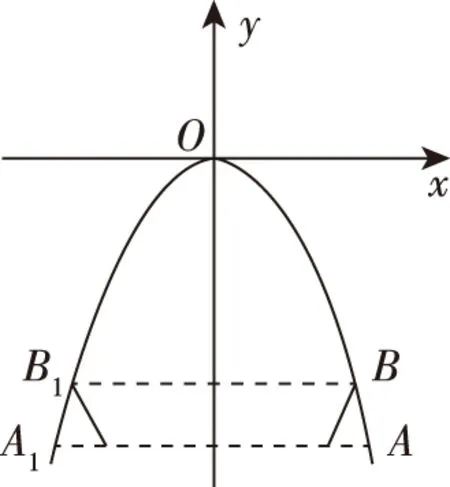
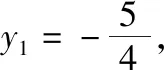
5.数学文化为提升素养之韵