高中生数学核心素养之运算能力现状及提高策略

广东

随着教育部制定的《普通高中数学课程标准》(2017年版)的颁布，数学的六大核心素养被正式确定下来，成为高中生学习数学的必备品格和关键能力，数学运算就是其中一种重要素养.

笔者从事高中数学教学十多年，明显感觉到高中生的运算能力在下降，这跟学生过早地接触电子计算设备，教学中教师和学生重笔算、轻估算，重结果、轻过程等原因有关.到了高中，教师们往往会忽视对运算能力的培养，学生觉得数学太难，考试得分总是很低，有些题明明会做，但是往往因为计算错误而拿不到分数.所以笔者认为，培养和提高高中生的运算能力势在必行.本文通过分析高中生数学运算能力的现状，进而提出高中学生数学运算能力的提高策略.

一、高中学生的数学运算能力现状

1.对数学运算的认识存在偏差

当今时代，计算机、手机、平板电脑等电子设备已非常普及，这些工具让日常计算方面的问题分分钟被解决，确实极大地改善了我们的生活面貌，但也会影响到在校的学生，使他们觉得凡是计算方面的问题都是小事，不值得重视，从而造成了对数学运算的忽视；还有一部分学生对于数学运算的过程是有畏惧心态的，觉得非常复杂难以掌握，而没有用心去感受那种由加减乘除、消元化简等运算步骤组成的环环相扣的数学逻辑之美，也感受不到科学的严谨性与合理性，凡此种种对于数学运算的认识方面的偏差，令学生们缺失了提升运算能力的动力和信心，直接导致了数学运算能力每况愈下，乃致恶性循环.

2.计算类的失误、错误较多

学生在做数学题时总会出现各种 “失误”，如题目数据看错了、公式写错了、最后的结果没有化简等等，这些问题在学生看来只是粗心大意导致的，下次做题认真细心就可避免，熟不知这样的问题是一直伴随着的，这种因为计算问题而导致的失误其实就是运算能力不足的一种表现，它暴露的是学生在计算原理、计算技巧等方面的基本功不扎实，面对限时作答，这个问题就被放大了，从而漏洞百出失误频频.

3.逻辑分析能力不强

一部分高中生在学习数学时会出现简单模仿的现象，即利用公式、法则或者定理机械生硬地套用、去解决具体问题，结果由于缺少了对题目前后逻辑的分析，往往顾此失彼，导致错解或少解，更麻烦的是这样的失误还不易察觉.

例如：过点A(4，-3)作圆(x-3)2+(y-1)2=1的切线，求此切线方程.在解该题时，一些学生只求到一条切线方程.而该题正确的做法是：①先判断A点与圆的位置关系，进而确定有2条切线；②再设定切线的点斜式方程，与圆的方程联立去解斜率k；③若解到两个不同的k,则解答完毕；若解到一个k值，则另一条切线方程是x=4.从以上分析可知，必须有①的前提，才能有③的正解，否则就会少算一解.所以说，若学生的逻辑分析能力不强、思维碎片化，运算结果必然会出问题.

4.对含参数类型的分类讨论的题目缺乏信心

数学高考共有六道解答题，其中那道以圆锥曲线为主要考查对象的解析几何题是很多学生的梦魇，基本上只能做答第一小问.这个题目的难点就是含参，运算过程中需要考生具备很强的分类讨论能力和字母运算能力，而这恰恰是学生们的薄弱环节，特别是字母运算能力因其庞杂的运算过程往往让学生产生畏难情绪，又因在平时的训练中对其算之甚少，导致考试时就更无信心、只能望题兴叹了.

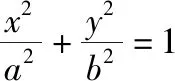
5.对于考试中出现的新型题、信息题反应迟缓

一般来说，在数学的考试中总会出现个别新颖的题目，或题型新、或思想新.它考查的是学生临场应变能力，而学生面对新型题或者信息题时，反应往往较为迟缓.

以上就是笔者对高中学生的数学运算能力现状所作的分析，形势不容乐观.经过长期的思考和实践，笔者认为可通过以下几个方面来提高学生的数学运算能力.

二、高中学生数学运算能力的提高策略

1.重视初、高中衔接，突破运算瓶颈

随着新的数学课程标准的发布，近些年对于义务教育的第二阶段即初中教育的内容及能力的要求有所降低，例如因式分解中的十字相乘法、配项分解法，与一元二次方程相关的判别式、根与系数的关系、含有参数的一元二次方程求根，圆的相交弦定理、弦切角，解不等式等等这些在初中的要求都大大降低了，甚至根本不用去讲，但这些内容在高中数学的学习中都要用到，而在高中教材里又没有专门的章节来讲这些内容，于是导致当用到这些知识的时候，学生的运算能力瓶颈就暴露了.由初中到高中，数学的难度是跨越式的，而非阶梯式的，这就要求高中教师要给学生提前做好初、高中数学知识的衔接，以保证学生在高中数学的运算中不会遇到知识性的困扰.

针对初、高中数学的衔接教学，教师可以去购买相关的书籍或者结合本校情况自己编写校本教材，建议在新高一开学第一周就把所有相关知识讲授完毕，当然也可以根据教学的进度适时的加入衔接知识，例如在讲一元二次不等式之前，再把一元二次方程相关的判别式、根与系数的关系、含有参数的一元二次方程求根等相关知识做个补充.总之，在高中数学教学时，教师要重视初、高中知识的衔接，这样才能让学生突破高中数学的运算瓶颈.

2.重视公式法则，夯实运算根基

对于数学的公式法则定理，教师除了强调其本身的应用外，还应该重视某些公式定理的生成过程或者证明过程，并且让学生也重视起来，只有这样才能夯实运算根基.例如：若a>0，且a≠1，M>0，N>0，那么loga(M·N)=logaM+logaN.这是对数的运算法则之一，这个法则不只结论是重要的，其证明过程也是重要的，因为它的证明过程不但给出了指数式与对数式互化的方法而且也揭示了指数与对数互化的本质，掌握了这个证明过程，就能理解指数式ab=N(a>0，且a≠1)与对数式b=logaN(a>0，a≠1，N>0)之间是一种等价关系.既精通定理法则的使用，又能理解其本身的证明过程，这对于学生更好地掌握算理算法是大有裨益的.

3.重视专题训练，提升运算能力

为了提升学生的运算能力，教师可以借助某些适合的知识模块来实现，把它当成专门训练运算能力和运算技巧的专题，搞所谓的“小题大做”.例如在处理椭圆和直线的位置关系时，就大有文章可做.椭圆相对于圆来说要复杂一点，但比起双曲线又要容易些，因此把“椭圆与直线位置关系”作为抓手，可以全面地去介绍并讲授数形结合、分类讨论、字母运算等众多的数学思想和数学方法.对于该专题的讲解切记要讲全、讲透、讲深.这里特别解释一下“讲全”，以椭圆的弦长问题为例：

①已知椭圆4x2+5y2=20的一个焦点为F，过点F且倾斜角为45°的直线l交椭圆于A，B两点，求弦长|AB|.(已知椭圆方程和直线方程，求弦长).

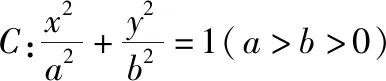
③已知椭圆4x2+5y2=20与过点(1, 0)的直线l交于A，B两点，且|AB|=3，求直线l的方程.(已知椭圆方程和弦长，求直线方程).

当讲完弦长公式后，教师要在某一次授课中就把这三个题全部涉及到(顺序最好是由易到难)，这样才能把椭圆中的弦长问题的小专题讲全面，进而帮助学生更好地提升运算能力，做到对同类型题的融会贯通.

4.重视运算技巧，突破运算难点

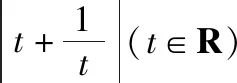
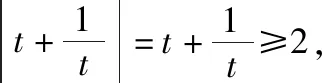
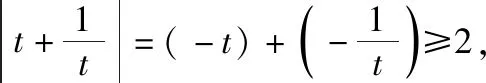
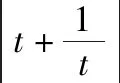
以上两种运算思路是不同的，后者更显技巧.由此可见所谓的运算技巧其实就是不同于常规的更简洁更高效的运算方法，这就要求学生在平时的训练中要有意识地进行一题多解的尝试，特别是那些运算复杂的题目，多角度思考、多想几种解法，对于提高运算技巧、突破运算难点是可行的.

5.重视经验积累，优化运算习惯

教师要去指导学生在高中数学的学习过程中，不断地、有意识地积累解题方法，总结运算经验，优化运算习惯.主要做法有：

①使用易错题集、典型题集.对于做错的题要有正确的认识和评价，有时算错一道题的收获其实比做对一道题的收获要大；

②养成高效读题和审题的习惯.一些应用题、创新题或者信息题，往往包含着对于解题有干扰的信息，这就要求学生具备在繁乱的题目叙述中快速捕捉到有用信息的能力；

③加强数学计算能力的训练.计算能力是运算能力的重要组成部分，是运算能力的基础，多记一些有关计算方面的结论，比如10以内的平方数、立方数，特殊值的角度弧度间的互化等等，有意识地培养口算心算的能力，注意提高对数学问题的可能结果的预判能力，从而养成好的运算习惯.