齐次化法巧解一类圆锥曲线问题

广东

直线与圆锥曲线是解析几何的两大研究对象，历年来都是高考的重点考查内容.考查方式多以直线与圆锥曲线的位置关系为背景显现，其一般的解题思路是直线与圆锥曲线联立方程组消元，通过韦达定理获得两根之间的关系，再利用已知条件求解，解答过程常常涉及繁冗运算，即使是在思路顺畅的情况下，也较难得出正确结果，因此提高运算能力与减少运算量是顺利解答解析几何题的必要条件.

要减少解析几何运算量，规避运算风险，算理就显得非常重要.本文以近两年圆锥曲线的高考题为例，提供一种通性的优化解法——齐次化法，它在解决两直线斜率之和(积)相关的定值、定点的圆锥曲线问题中常能达到化繁为简、举重若轻的效果.

一、两种解法比较

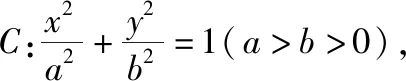
(Ⅰ)求C的方程；

(Ⅱ)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

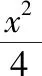
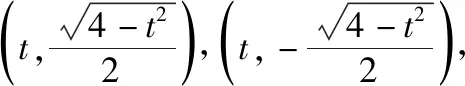
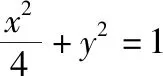
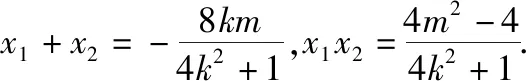
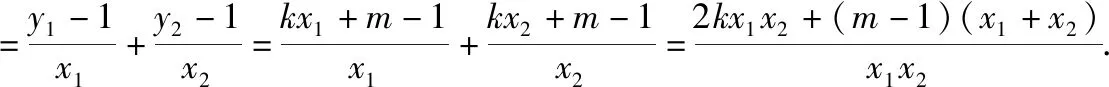
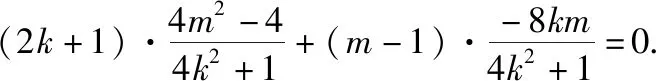
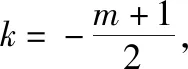
解法二：(齐次化解法)设直线l的方程为mx+n(y-1)=1.

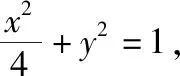
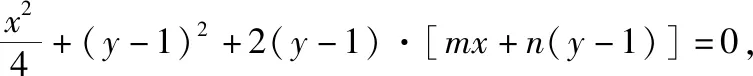
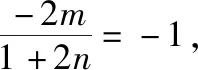
所以直线l过定点(2,-1).

评析：(1)解析几何的综合题往往有多种解法，关键是找到一种最有效的解题途径.从示例可以看出齐次化解法的代数变形较为简单，运算量较少，解题过程更为简洁.

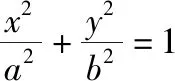
①设直线方程为m(x-x0)+n(y-y0)=1，其中(x0,y0)为两相关直线的交点(这样设直线方程的形式，右边为1对联立齐次化较为方便)；

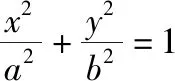
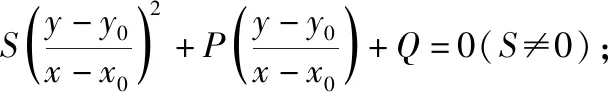
⑤根据题目条件进一步求解.

注：当两相关直线的交点(x0,y0)不在原点时，可以通过平移坐标系的方式，将交点(x0,y0)变为原点，再齐次化解答，这一方法也称“平移齐次化”法.但这样多了一个坐标的相互变换，思维强度加大.

二、齐次化法的应用

1.两直线的斜率之积为定值型

例1(2017·全国卷Ⅲ理·20)已知抛物线C：y2=2x，过点(2,0)的直线l交C于A,B两点，圆M是以线段AB为直径的圆.

(Ⅰ)证明：坐标原点O在圆M上；

(Ⅱ)设圆M过点P(4,-2)，求直线l与圆M的方程.

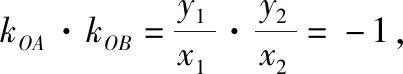
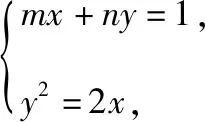
故kOA·kOB=-2m=-1，所以OA⊥OB，即坐标原点O在圆M上.

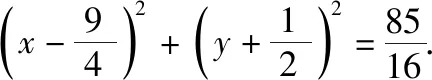
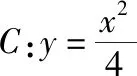
(Ⅰ)求直线AB的斜率；

(Ⅱ)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程.

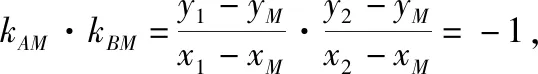
解答:(Ⅰ)略解，得直线AB的斜率为1.

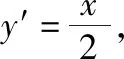
设直线AB的方程为m(x-2)+n(y-1)=1，因为直线AB的斜率为1,易得m=-n.

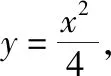
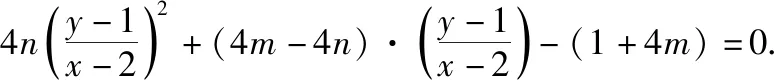
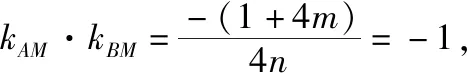
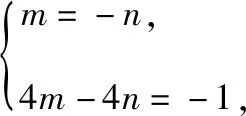
2.两直线的斜率之和为定值型

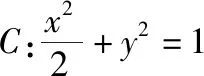
(Ⅰ)当l与x轴垂直时，求直线AM的方程；

(Ⅱ)设O为坐标原点，证明：∠OMA=∠OMB.

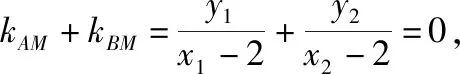
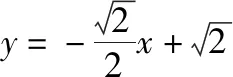
(Ⅱ)设直线AB的方程为m(x-2)+ny=1，因为直线AB过点F(1,0),易得m=-1.

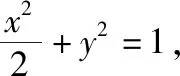
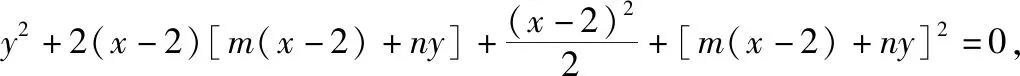
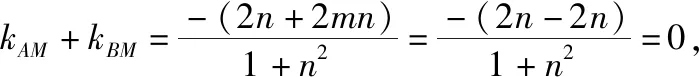
例4(2018·全国卷Ⅰ文·20)设抛物线C：y2=2x，点A(2,0),B(-2,0)，过点A的直线l与C交于M,N两点.

(Ⅰ)当l与x轴垂直时，求直线BM的方程；

(Ⅱ)证明：∠ABM=∠ABN.

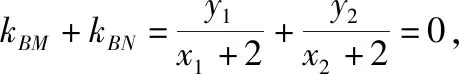
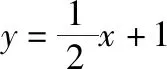
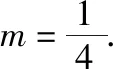
由y2=2x，变形得y2=2(x+2-2)，整理得y2=2(x+2)-4，

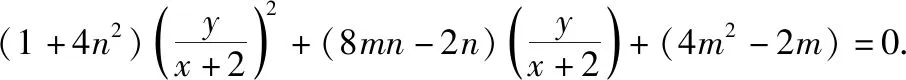
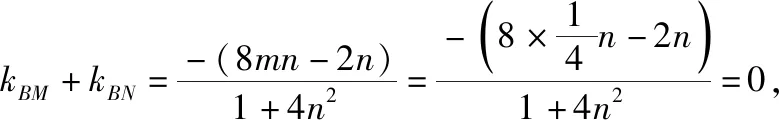
三、小结反思

圆锥曲线中涉及两直线斜率相关的定值、定点问题，是高考的热门考点.从上述例子可以看出，全国卷2017,2018年文、理共12份试卷的解析几何大题中(共9题，其中有3份试卷的题目一样)，连续两年共考查了5次的两直线斜率相关的定值、定点问题.因此，对于高考真题不能浅尝辄止，特别是高频考点，要认真分析体会题目的内涵与考查背景，掌握其典型解法等等.

与两直线斜率相关的定值、定点问题重点考查方程思想，转化与化归思想等，往往需要学生具备较强的知识综合性，较高的思维能力与运算能力，而齐次化法可以将此类问题统一处理，是一种通性解法，运算量较少，既可以简化解题过程，又可以培养学生的思维灵活性，应该熟练掌握.

四、练习巩固

最后提供四题作为练习，以加深体会齐次化法在圆锥曲线中的妙用.

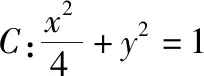
(Ⅰ)若x1=0，求△OAB的面积；

(Ⅱ)在x轴上是否存在定点T，使得直线TA,TB与y轴围成的三角形始终为等腰三角形.

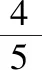
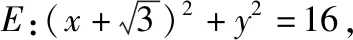
(Ⅰ)求C的方程；

(Ⅱ)已知过点(2,-1)的直线l与C交于两点A,B，M是C与y轴正半轴的交点，设直线MA,MB的斜率分别为k1,k2，证明：k1+k2为定值.

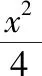
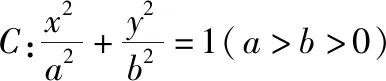
(Ⅰ)求椭圆C的方程；

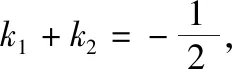
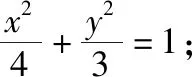
4.已知抛物线C：y2=2px(p>0)，三点P1(3,2),P2(1,-2),P3(1,2)中只有一个点不在抛物线上.

(Ⅰ)求C的方程；

(Ⅱ)设过P1且不过P2,P3的直线l与C交于A,B两点，若直线P2A,P2B的斜率分别为k1,k2，证明：k1k2为定值.