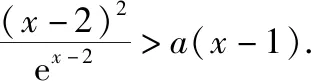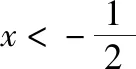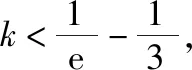解决存在整数解时参数取值范围问题的利器

陕西

自从2015年全国卷Ⅰ理科第12题考查了函数存在唯一一个整数解时参数的取值范围问题，随之一些模拟题中也出现了一些类似的问题.笔者经过归纳梳理，探索出解决这类问题的一些规律，一般有如下三种常见方法.

一、利器之一——分离参数法

例1.(2017·四川二模)已知函数f(x)=(3x+1)ex+1+mx，若有且仅有两个整数解使得f(x)≤0，则实数m的取值范围是

( )

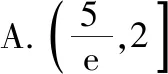
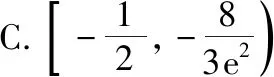
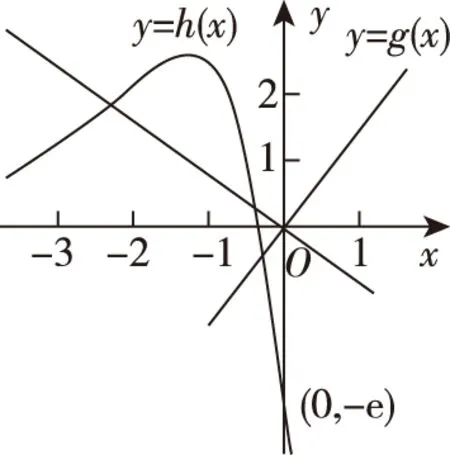
【分析】本题属于函数存在两个整数解，求参数的取值范围问题.先根据条件将参数m分离出来，得到g(x)=mx，h(x)=-(3x+1)ex+1，然后利用导数研究函数y=h(x)的单调性和极值，在同一平面直角坐标系中作出y=h(x)，y=g(x)的大致图象，通过观察得到函数存在两个整数解时，参数m满足的不等式组，进而解出实数m的取值范围.

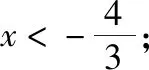
例2.已知f(x)=xlnx-ax+a，若f(x)<0仅有三个整数解，则实数a的取值范围是

( )

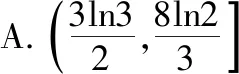
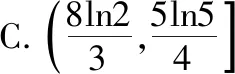
【分析】本题属于函数存在三个整数解，求参数的取值范围问题.先根据条件将参数m分离出来，得到g(x)=xlnx，y=ax-a，然后利用导数研究函数g(x)=xlnx的单调性，根据已知条件得到函数存在三个整数解时，参数a满足的不等式组，进而解出实数a的取值范围.

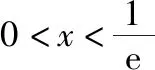
【方法提升】上述两个例题都是求参数的取值范围，例1是函数存在两个整数解，例2是函数存在三个整数解，解决的方法都是先分离参数，然后借助导数研究函数的单调性，根据已知条件中整数解的情况，有时也借助图象列出满足条件的不等式组，进而解出参数的取值范围.

二、利器之二——数形结合法

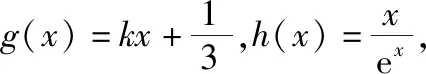
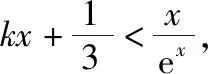
对于新闻编辑工作人员来说，要不断提高自己的业务能力，新形势下，新闻编辑工作人员要学会使用数字技术去发现新闻，编辑新闻，做好新闻的宣传工作。传统报业只有充分利用网络优势，才能促进自身的发展。网络传播非常快，而且时效性比较强，传统报业和新媒体的融合不能仅仅依靠传统的报纸新闻传播这种途径，而是要充分利用互联网信息的平台，大大提升新闻报道的速度，打破传统纸媒的天花板。另外，随着数字技术的发展，新闻的传播速度越来越快，信息的价值也在逐渐增强。传统报纸要充分利用数字信息技术制作新闻，摒弃传统的单一渠道，充分开发新闻价值。

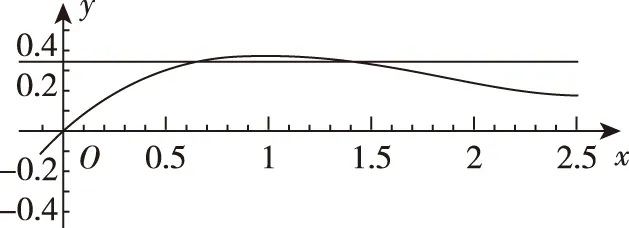
【方法提升】上述例题属于函数存在一个整数解，求参数的取值范围问题.先根据条件将参数分离出来，得到两个函数，然后作出两个函数的图象，通过观察图象得到函数存在一个整数解时，参数满足的不等式组，进而解出参数的取值范围.

三、利器之三——猜想验证法

例4.(2018·成都市理科)在关于x的不等式e2x2-(aex+4e2)x+aex+4e2>0(其中e=2.718 28…为自然对数的底数)的解集中，有且仅有两个大于2的整数，则实数a的取值范围是

( )

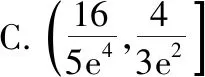
【分析】本题属于函数存在两个大于2的整数解，求参数的取值范围问题.先根据满足条件的x逐一代入验证判断是否符合题意，只要找到满足条件的x的值，对应的参数a的取值范围也就确定了.

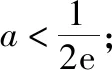
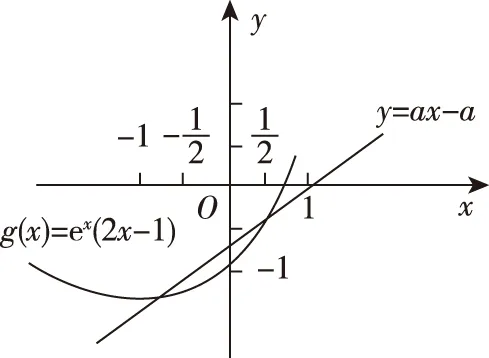
例5.(2015·全国卷Ⅰ理·12)设函数f(x)=ex(2x-1)-ax+a，其中a<1，若存在唯一的整数x0，使得f(x0)<0，则a的取值范围是

( )

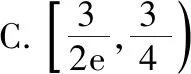
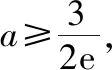
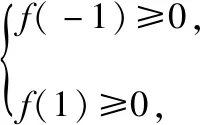
【方法提升】上述两个例题都是求参数的取值范围，例4是函数存在两个整数解，例5是函数存在唯一一个整数解，解决的方法都是先根据满足条件的x逐一代入验证判断是否符合题意，通过猜想只要找到满足条件的x的值，对应的参数的取值范围就随之确定了.