减元借参，构造函数解决双极值点问题

广东

双极值点问题在近几年高考及各种模拟考试中，常作为热点和重点题型考查. 此类问题变化多样，有些题型不含参数，但更多的题型含有参数. 双极值点其本质为函数的双零点，是一个多元数学问题，不管待证的是两个变量的不等式，还是导函数的值的不等式，解题的策略都是转化为一元变量问题求解，途径都是构造一元函数. 含参数的极值点问题，在原有的两个变量x1,x2的基础上，又多了一个参数，解题思路自然就会想到消参数，从而转化成不含参数的问题去解决；或者以参数为媒介，构造出一个变量的新函数. 下面本文逐一探索解题策略.

一、转化为x1或x2的一元函数

思路：极值点的本质为导函数的零点.对于双极值点，则有f′(x1)=f′(x2)=0，借助此特殊关系，可把关于x1,x2的二元函数问题转化为关于x1或x2的一元函数问题，进而构造新函数，研究新函数的单调性和最值即可得到结论.

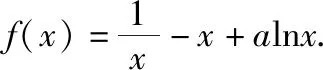
(Ⅰ)讨论f(x)的单调性；

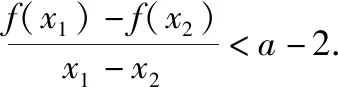
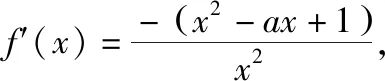
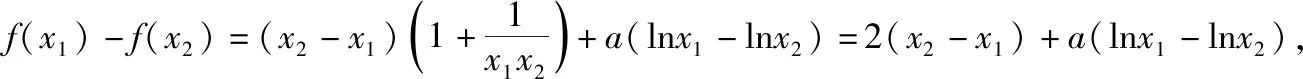
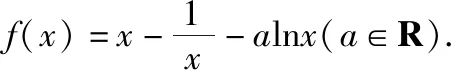
(Ⅰ)讨论函数f(x)的单调性；

(Ⅱ)若f(x)有两个极值点x1,x2，记过点A(x1,f(x1)),B(x2,f(x2))的直线斜率为k,问：是否存在a，使得k=2-a？若存在，求出a的值；若不存在，请说明理由.

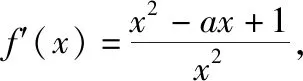
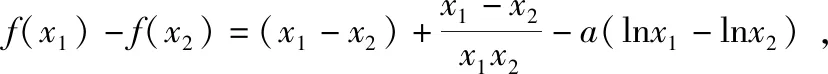
二、转化为第三变量的一元函数

思路：原函数解析式一般含有第三变量a，若导函数的本质为二次函数，则两个极值点x1,x2和a之间存在韦达定理关系；若导函数的本质不是二次函数，也会有f′(x1)=f′(x2)=0，借助此方程关系，也把待解决的问题转化为自变量为a的函数，研究其单调性和最值解题.

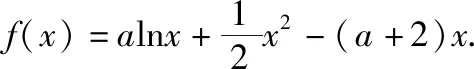
(Ⅰ)若曲线y=f(x)在点(1，f(1))处的切线经过坐标原点，求实数a的值；

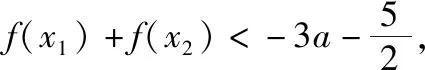
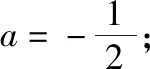
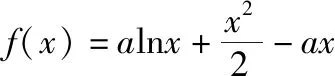
(Ⅰ)求实数a的取值范围；

(Ⅱ)设f(x)的两个极值点分别为x1,x2，若不等式f(x1)+f(x2)<λ(x1+x2)恒成立，求λ的最小值.

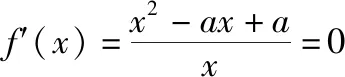
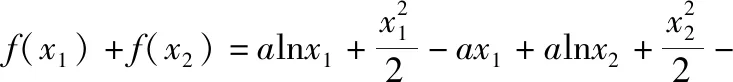
三、化归为统一结构，进而构造函数

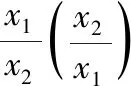
例5.(节选自2010·天津卷理·21)已知函数f(x)=xe-x(x∈R)，如果x1≠x2，且f(x1)=f(x2)，证明：x1+x2>2.

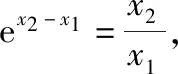
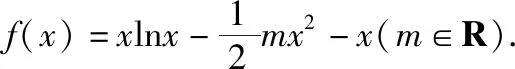
(Ⅰ)若函数f(x)在(0，+∞)上是减函数，求实数m的取值范围；

(Ⅱ)若函数f(x)在(0，+∞)上存在两个极值点x1，x2，且x12.

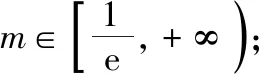
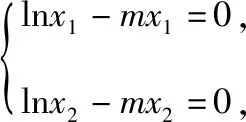
四、两边分别变形为x1,x2的相同结构式，进而构造函数

思路：双极值点问题，除了转化为单一变量函数，还可以保留双变量，分别对不等号两边进行变形，当两边结构一致时，转化为研究函数的单调性问题，进而构造新函数也可得到结论.

例7.(节选自2016·全国卷Ⅰ理·21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点x1,x2，证明：x1+x2<2.

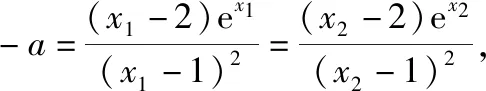
例8.已知函数f(x)=x2-2x+alnx.

(Ⅰ)讨论函数f(x)的单调性；

(Ⅱ)若函数f(x)存在两个极值点x1,x2，且x1x2f(x1).

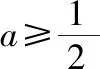
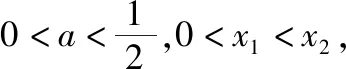
五、利用对数平均不等式链

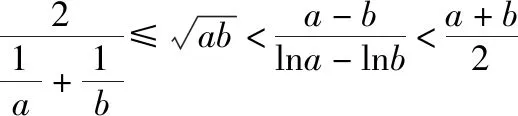
例9.题目同例1.

分析：(Ⅰ)见例1；

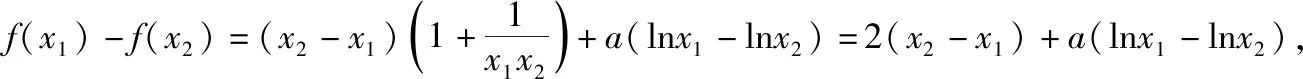
例10.题目同例7.

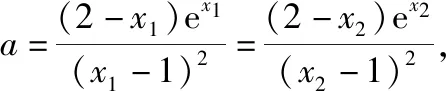
由(x1-1)2+(x2-1)2>0,4-(x1+x2)>0得x1+x2<2，证毕.