从一道圆锥曲线解答题谈解析几何备考策略
甘肃
2018年数学全国卷Ⅲ理科第20题总体上保持了近几年来的命题特色,是一道直线与椭圆的位置关系的问题,并以中点弦问题为依托,主要考查了直线与椭圆的位置关系以及等差数列,体现了高考试题在知识交汇处命题的特点,考查了数形结合思想,也考查了考生的数学抽象、逻辑推理和数学运算的核心素养.其中,第(Ⅰ)问容易入手,第(Ⅱ)问难度较大,前后两问之间有很好的梯度性,具有很好的选拔功能.本文对这道试题进行解法、源头和变式探究,并结合这道试题来谈一下解析几何的备考策略.
一、真题再现
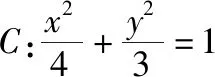
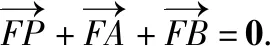
二、解法探究
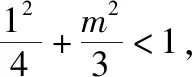
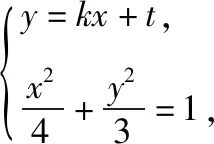
则Δ=64k2t2-4(4t2-12)(3+4k2)>0,得
4k2+3>t2, ①
因为m>0,所以t>0,k<0,
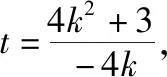


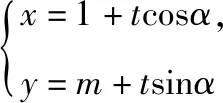
整理可得(3cos2α+4sin2α)t2+(6cosα+8msinα)t+4m2-9=0,
由t的几何意义知|MA|=|t1|,|MB|=|t2|,因为点M在椭圆内,这个方程必有两个实根,
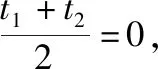
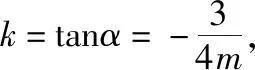
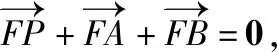
因为M(1,m),F(1,0),所以P的坐标为(1,-2m),
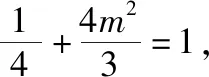
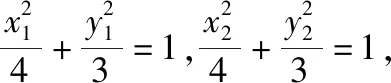
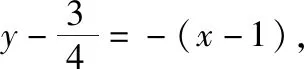


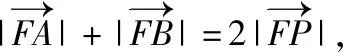
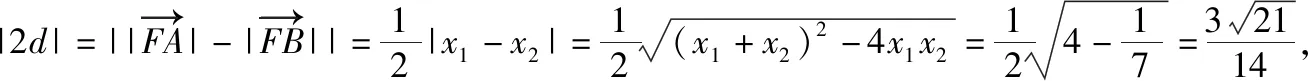

【解法赏析】第(Ⅰ)问的证法1运用了点差法,点差法可以看成破解圆锥曲线中点弦问题的通法;第(Ⅰ)问的证法2运用了线参法,将直线方程和椭圆方程联立后运用韦达定理和坐标运算,发挥判别式的制约作用;第(Ⅰ)问的证法3运用了参数方程法,令人耳目一新.第(Ⅱ)问既运用了点差法,又运用了线参法,利用等差中项的定义证明了等差数列,体现了函数与方程、化归与转化的思想.从以上可以看出,选择的解法不同,运算的繁琐程度不同.本题中的运算是借助几何图形进行的代数运算,考查了运算求解能力,体现了数学运算的核心素养.解析几何的运算通常集“繁、长、巧”于一体,让很多同学望而生畏.究其原因,主要是同学们在运算量的判断上出了问题,不能预估所选的解题方法会有怎样的运算量.若在解题过程中,同学们能认识到解题环节产生的运算,并通过分析进行合理的调控,更深入地理解运算方法,这样就可以提高运算的灵活性.
三、源头探究
“问渠那得清如许?为有源头活水来” .接下来探索这道题的源头,揭开这道题的“庐山真面目”.
1.源头1
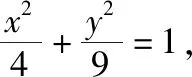
(1)这组直线何时与椭圆相交?
(2)当它们与椭圆相交时,证明这些直线被椭圆截得的线段的中点在一条直线上.
真是“众里寻它千百度,那题却在课本习题处”,也体现了“高考题源于课本,高于课本”.
2.源头2
在历年高考真题中,也有该高考题的“影子”:(2015·全国卷Ⅱ理·20):
已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(Ⅰ)证明:直线OM的斜率与l的斜率的乘积为定值;

通过探源,我们发现这道题既可以看成改编自课本,也可看成改编自历年高考真题.
四、变式探究
圆锥曲线有很多类似的性质,笔者模仿命题者的命题思路,对以上试题进行改编,得到一道变式题.
变式已知斜率为k的直线l与抛物线C:y2=4x交于A,B两点,线段AB的中点为M(1,m)(m>0).
(Ⅰ)证明:k>1;
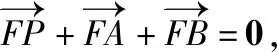
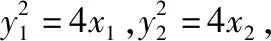

因为点M在抛物线C内,所以m2<4,结合m>0,所以0 所以k>1. (Ⅱ)由题设可得F(1,0),设P(x0,y0), 所以x0=1,y0=-2m, 因为点P在抛物线C上,所以(-2m)2=4,解得m=1,所以P(1,-2), k=2, 所以直线l的方程为y-1=2(x-1),即y=2x-1, 近几年高考数学试题遵循“大稳定,小创新”的方针,重视基础知识和基本技能的考查.同时,通过上面对圆锥曲线真题的分析,发现该真题源自课本.因此回归课本应贯穿圆锥曲线复习的始终.因为课本是数学知识的“生长地”,课本是高考复习的“根据地”,课本是高考试题的“策源地”,回归课本是高考复习的起点,从高考的要求出发,把课本熟化,公式定理能信手拈来,基本题型能“借题发挥”.在回归课本的基础上,要着重强化对知识的梳理、优化知识结构、构建知识网络. 高考中解析几何试题通常是对常见题型进行加工改编,通过对基础知识的整合、变式和拓展,加工为高立意、新情境、巧设问的解析几何问题,坚持新题不难,难题不怪的命题方向.这要求同学们通过高中的学习掌握基础知识、基本概念、基本技能和基本数学思想,通过对教材中基本例、习题的变通,积累常规问题的解法,反复体会其中蕴含的思维方法.把解题方法提高到数学思想的高度,提高分析和解决综合问题的能力.例如,对于圆锥曲线的中点弦问题,要优先考虑点差法.对于求椭圆离心率的题目,大多要利用数形结合法,结合椭圆的定义求解.对于抛物线的焦点弦和焦半径问题,要根据焦点弦公式和焦半径公式,并结合抛物线定义求解.在求椭圆的弦长时,利用弦长公式,运用设而不求的方法求解. 高考数学答卷中反映出的问题之一是部分考生的运算能力差,有的考生想的很好,但运算不过关,一遇到复杂试题,从一开始就错,并且自己没有自查能力,一直错到底.而出错的原因往往很明显,就是诸如一个符号的问题,直线方程和圆锥曲线方程联立化简整理时出错.数学运算能力的培养不仅仅是高三复习的事,更应该贯穿于高中数学学习的始终.特别是解析几何解答题,综合性强,代数推理和运算求解能力要求高,繁杂和冗长的计算是必不可少的,因此同学们要通过强化数学思想方法,特别是函数与方程、数形结合、等价转化、分类讨论等的理解与应用,从而提高自己的运算求解能力,培养自身的数学运算核心素养. 高考试题不仅具有选拔功能,还具有很好的教育功能.高考试题凝结了命题专家的智慧与匠心,具有较强的原创性与指导意义,有利于考查考生的探究意识与创新精神.有部分高考试题是往年真题的同类题或“翻版”, 因此,在平时的学习中,对高考试题进行适当发散研究,不仅可以理清脉络,把握高中数学主干知识,避免高三复习的随意性、盲目性,而且可以有效训练考生的数学思维,提高探究能力,培养创新意识.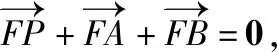
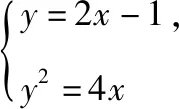
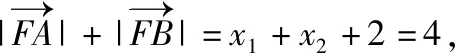

五、对2019年备考策略的建议
1.回归课本,夯实基础,构建知识网络
2.注重通性通法
3.提高数学运算求解能力,培养数学运算的核心素养
4.研究历年高考真题,体会命题专家的命题思路
5.重视选修知识,关注知识交汇


