一类静电势方程的后验误差上界估计

房明娟， 阳 莺

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

Poisson-Nernst-Planck (PNP)方程是由Poisson方程和Nernst-Planck (NP)方程耦合而成的一类重要的非线性偏微分方程系统，常用来描述电扩散模型。该模型在半导体、电化学系统和生物膜通道等方面起着至关重要的作用。

由于PNP方程的耦合性和非线性，该方程的求解较为困难，且只有在极少情况下有解析解。早期的研究者提出了一系列求解PNP方程的方法，包括有限元方法、有限差分方法、边界有限元方法、有限体积方法等。有限元方法因适用于处理不规则几何形状和复杂边界问题而被广泛应用，在求解某些生物分子系统PNP方程取得了很好的效果。但是有限元计算的主要难点之一是实际问题的分子电荷很多，使得PNP方程具有强奇性，从而使经典的有限元方法无法有效应用于实际计算，而自适应有限元方法是当前广泛使用的解决奇性问题的最有效的方法之一。

近年来，自适应有限元方法得到了极大的发展[1]，利用自适应有限元方法可以在很大程度上提高计算性能。自适应有限元方法通过计算每个单元上的后验误差估计子获得每个单元的误差范围，从而对网格进行局部加密和放粗，提高计算效率，因此其在科学和工程计算中有着十分重要的应用价值。

后验误差估计作为自适应有限元计算的核心步骤，通常被作为自适应有限元方法中网格加密或放粗的指示子，后验误差估计的方法可以为自适应有限元方法的网格加密提供一个有效的加密策略。后验误差估计子包括多种类型，通过计算局部区域残量得出误差估计的方法称为残量型后验误差估计[2]。Babuska等[3]于1986年最早提出了残差法。Zienkiewicz等[4]在1987年提出了基于后处理技术的后验误差法，由于其计算简单，易于理解，因而受到研究者的极大关注。如文献[5]在不规则网格中研究了一类Poisson方程有限元逼近的梯度恢复型后验误差估计。文献[6]研究了非协调有限元逼近的梯度恢复型后验误差估计。为此，利用梯度恢复算子，采用后处理方法，对PNP方程中的静电势进行后验误差上界估计。

1 预备知识

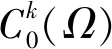
其中，1≤p≤∞。Lp(Ω)空间的范数为

当p=2时，L2(Ω)为偏微分方程中一重要空间，该空间内积为

∀u,v∈L2(Ω)。

定义广义导数Dαv为

Sobolev空间Wm,p(Ω)为

Wm,p(Ω)={v:Dαv∈Lp(Ω),|α|≤m},

范数为：

半范数为：

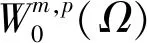
考虑如下稳态PNP方程：

(1)

(2)

(φ,∀

(3)

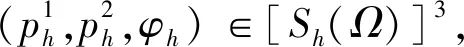
(4)

(φh,∀

(5)

2 上界估计

为了方便证明，令Th={τ}为Ω上进行的均匀的三角剖分的网格，且网格大小h>0，hτ为单元τ的直径，hl为三角形单元落在边界∂Ω上的边长度，∂2Th为网格上所有节点的集合，Λ=∂2Th∂Ω，φz为Sh中节点z∈∂2Th处的基函数，则对任意的z∈∂2Th，l∈∂Th,τ∈Th，有

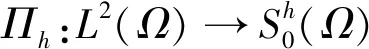
∀v∈L2(Ω)，

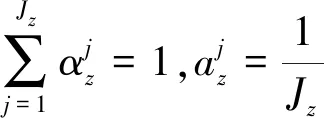
Ghv=Πh(v), ∀

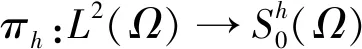
引理2[9-10](Poincare不等式) 设Ω为边界∂Ω上Lipschitz连续的有界区域，则存在正常数C，使得

‖u‖0,p,Ω≤C‖u‖0,p,Ω+

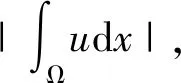
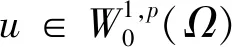
‖u‖0,p,Ω≤C‖u‖0,p,Ω，∀u∈W1,p(Ω)，

‖

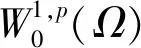
其中，

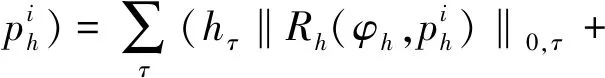
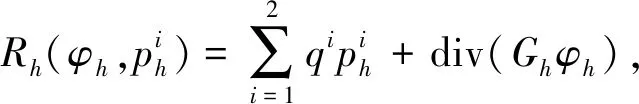
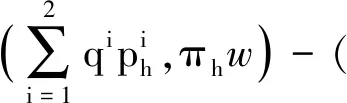
(6)

根据方程(5)可得

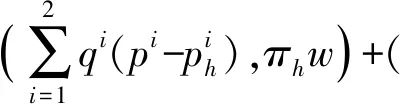
(7)

(Ghφh,-(πhw-w))=

(8)

将式(8)代入式(7)，并应用引理1可得

div(Ghφh)‖0,τhτ+‖φh-Ghφh‖0,τ)‖w‖1,wτ+

令w=φ-φh，应用Poincare不等式，可得到定理1的结论。证毕。

利用定理1的后验误差估计子，可设计出PNP方程的一类自适应有限元算法。

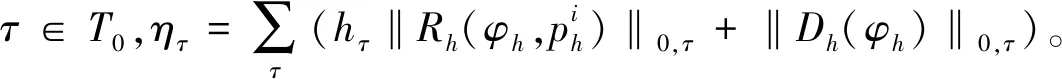
1)有限元计算。在初始网格T0上进行有限元计算，得到有限元解φh。

2)误差估计。在每个单元τ∈T0上计算后验误差估计子ητ。

算法1通常取θ=1/2，δ为给定的精度。应用算法1，根据所证得的有效的后验误差估计子，便可得到更为精确的解。

3 结束语

利用梯度恢复型方法，给出了PNP方程中静电势方程的后验误差上界估计，构造了静电势方程的后验误差估计子，设计了相应的自适应有限元算法。而对于基于梯度恢复型后验误差估计子设计的自适应有限元算法，后续工作将通过数值实验验证其有效性。