基于图模型的传感器节点定位方法

赵海兵， 蒋俊正

(桂林电子科技大学 信息与通信学院, 广西 桂林 541004)

无线传感器网络(wireless sensor network,简称WSN)备受关注，已广泛应用于军事、环境、医疗、家居和工业等领域[1-2]。在很多需要WSN提供监测服务的场景下，不含位置信息的监测数据是缺乏应用价值的。例如环境污染监测、森林火灾监测和天然气管道监测等应用场景中，WSN中的传感器节点不仅需要提供监测对象的信息，还要包含节点自身的位置信息。因此，WSN中传感器节点定位技术的研究就显得尤为重要。

WSN中传感器节点位置的获取可以借助于中国北斗导航系统(Beidou navigation satellite system,简称BDS)[3]或美国全球定位系统(global positioning system,简称GPS)[4]，但需要在传感器中添加BDS或GPS接收模块，不仅增加了传感器的制作成本，还增加了本身的功耗，缩短整个WSN的寿命。而且部署传感器的具体环境可能是复杂多变的，如室内环境或山林地区，BDS和GPS信号难以有效穿透墙体、高山、密林等障碍，这导致很多场景下无法使用BDS和GPS进行定位[5]。针对这一系列问题，常用的做法是只在少数传感器中添加定位模块，并将其部署在可以接收BDS或GPS信号的位置，利用这一部分传感器节点的位置和节点间距离对其他节点进行定位。其中，事先获知位置的传感器节点称之为已知位置(location-aware,简称LA)节点，其他节点称为未知位置(location-unaware,简称LU)节点。节点间测距的方法有到达时间(time-of-arrival,简称TOA)、到达时间差(time-difference-of-arrival,简称TDOA)、到达角(angle-of-arrival,简称AOA)和接收信号强度(received-signal-strength,简称RSS)[6-7]等。

现有的众多定位方法中，许多文献把定位问题归结为了优化问题，采用凸优化的方法进行求解。例如，BISWAS等[8]采用了半正定规划(semi-definite programming,简称SDP)松弛的方法，且引入了一个正则项，有助于降低SDP解决方案的秩，最后采用梯度下降法细化节点位置，提高了定位的准确性。但该正则项系数的选取比较繁琐，增加了计算的复杂度。NONGPIUR[9]同样采用了SDP松弛的方法，不同的是从节点连通性出发引入了一个全新的正则项，用于惩罚一些孤立的节点，提高了定位的准确性，该正则项系数的选取没有经过复杂的运算，但只是依据经验获取，更合理的选取方式有待进一步研究。TSENG[10]采用了二阶锥规划(second-order cone programming,简称SOCP)松弛的方法，比SDP松弛有更少的变量和约束条件，但若有大量LU节点分布在LA节点形成的凸包之外，则不会有良好的定位效果[11]。

区别于上述定位方法都有约束条件的限制，同样采用节点间的距离误差作为目标函数，而将定位问题归结为一个无约束的优化问题。该方法在图模型基础上充分考虑了节点间的连通性，利用节点间距离对目标函数中各求和项设置了归一化的权重值。对该优化问题目标函数的求解分为两步：1)利用三点定位法对LU节点进行简单粗略的初步定位；2)把基于三点定位得出的初步定位结果作为初始值，结合二阶泰勒近似给出的修正海森矩阵，采用修正牛顿法对定位问题进行求解。仿真结果表明，与文献[8]相比，本方法在不同程度的测距误差下定位更准确，且算法迭代次数更少，耗时更短。

1 定位问题的图模型

为模拟某一实际区域内的WSN，在[-0.5,0.5]×[-0.5,0.5]的平面内构建了WSN的图模型G=(V,E,W)，将实际环境中传感器近似为平面区域内的节点，模拟实际场景中传感器的部署方式，将传感器的位置近似为平面区域内的坐标位置。

V={x1,x2,,xN,a1,a2,,aM}是WSN中所有传感器节点的集合。其中：N个LU节点是随机分布的，记xi=[xi1;xi2]，xi1和xi2分别为第i个LU节点的横坐标和纵坐标；M个LA节点的位置假设是准确的(或其位置误差可以忽略不计)，记ak=[ak1;ak2]，ak1和ak2分别为第k个LA节点的横坐标和纵坐标。则N个LU节点和M个LA节点的坐标位置分别表示为x和a，即

x=[x11,x12,x21,x22,,xN1,xN2]T，

(1)

a=[a11,a12,a21,a22,,aM1,aM2]T。

(2)

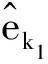
(3)

xTCika-aTDkix+aTFkka，

(4)

其中，

Aij=(ei1-ej1)(ei1-ej1)T+

(ei2-ej2)(ei2-ej2)T，

(5)

(6)

(7)

在实际场景中，如果2个传感器节点间的距离太大，发射信号功率可能会衰减至不能被识别到，因此并不是所有的节点都可以互相通信。假设只有距离在dmax范围内的两节点才可以正常通信，并用一条边相连接，记为E={ρij,ρik}，其中ρij表示第i个LU节点和第j个LU节点有一条边相连，ρik表示第i个LU节点和第k个LA节点有一条边相连，从而把WSN建模成一个彼此相连的通信网络图。基于节点网络图的连通性，把直接相连的节点作为邻居节点，也就是可以直接相互通信的节点，如下所示：

N1(i)={j:ρij∈E}，

(8)

N2(i)={k:ρik∈E}，

(9)

N(i)=N1(i)∪N2(i)。

(10)

其中，i=1,2,,N,N(i)中包含了第i个LU节点的所有邻居节点，即N1(i)包含了可以与第i个LU节点直接相互通信的所有LU节点，N2(i)包含了可以与第i个LU节点直接相互通信的所有LA节点。

由于WSN以无线的方式进行通信，且节点发射信号的功率和接收到信号的功率都可以测得，节点间距离可以通过RSS测距技术[6]获取。但是在现实环境下，发射信号在传输过程中易受多径衰落和阴影衰落等影响，所以根据信号的衰减特性测得的距离并非两节点间的真实距离。于是，考虑到节点间距离越远，测距时受到干扰的不确定性越大，测距数据越不可靠，则节点间的测得距离dij和dik可表示为[8]：

(11)

(12)

εijorεik=2rand(1,1)-1。

(13)

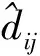
(14)

(15)

综上，本方法构建了WSN图模型G=(V,E,W)。从而定位问题可以概述为：基于图的网络拓扑结构，利用LA节点的坐标位置和RSS技术测得的节点间距离，求解LU节点的坐标位置。

2 定位问题的求解

基于图模型G=(V,E,W)，最小化邻居节点间距离误差的加权和[8]，将定位问题归结为无约束优化问题：

(16)

显然，该目标函数(16)是关于LU节点坐标x的高度非线性四次函数，可以通过二阶泰勒展开将其近似为如式(17)，再通过迭代的方法求最优解[12]。

f(x)≈f(x0)+Tf(x0)(x-x0)+

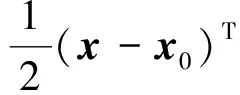
(17)

为此，采用两步法来求解。

2.1 初始值x0的选取

结合泰勒级数和泰勒展开式的性质[13]，式(17)中选取的x0需在x附近，即作为迭代初始值的x0需在LU节点位置附近，因此对LU节点进行粗略的初步定位。

当待求LU节点最大测距范围内至少有3个LA节点时，选取距其最近的3个LA节点，采用三点定位法对该LU节点进行定位。三点定位的几何思想是：在平面内分别以3个LA节点为圆心，以LA节点和LU节点的距离为半径，画圆，3个圆的交点就是待求的LU节点。三点定位方法如图1所示，A、B和C表示3个LA节点，坐标位置依次是(x1,y1),(x2,y2),(x3,y3)；P为LU节点，A、B和C三点到待求节点P的距离分别为d1,d2,d3。假设待求节点P的坐标位置为(x,y)，则可得到3个关于圆的方程组：

(18)

对式(18)求解，可得LU节点P的具体坐标：

(19)

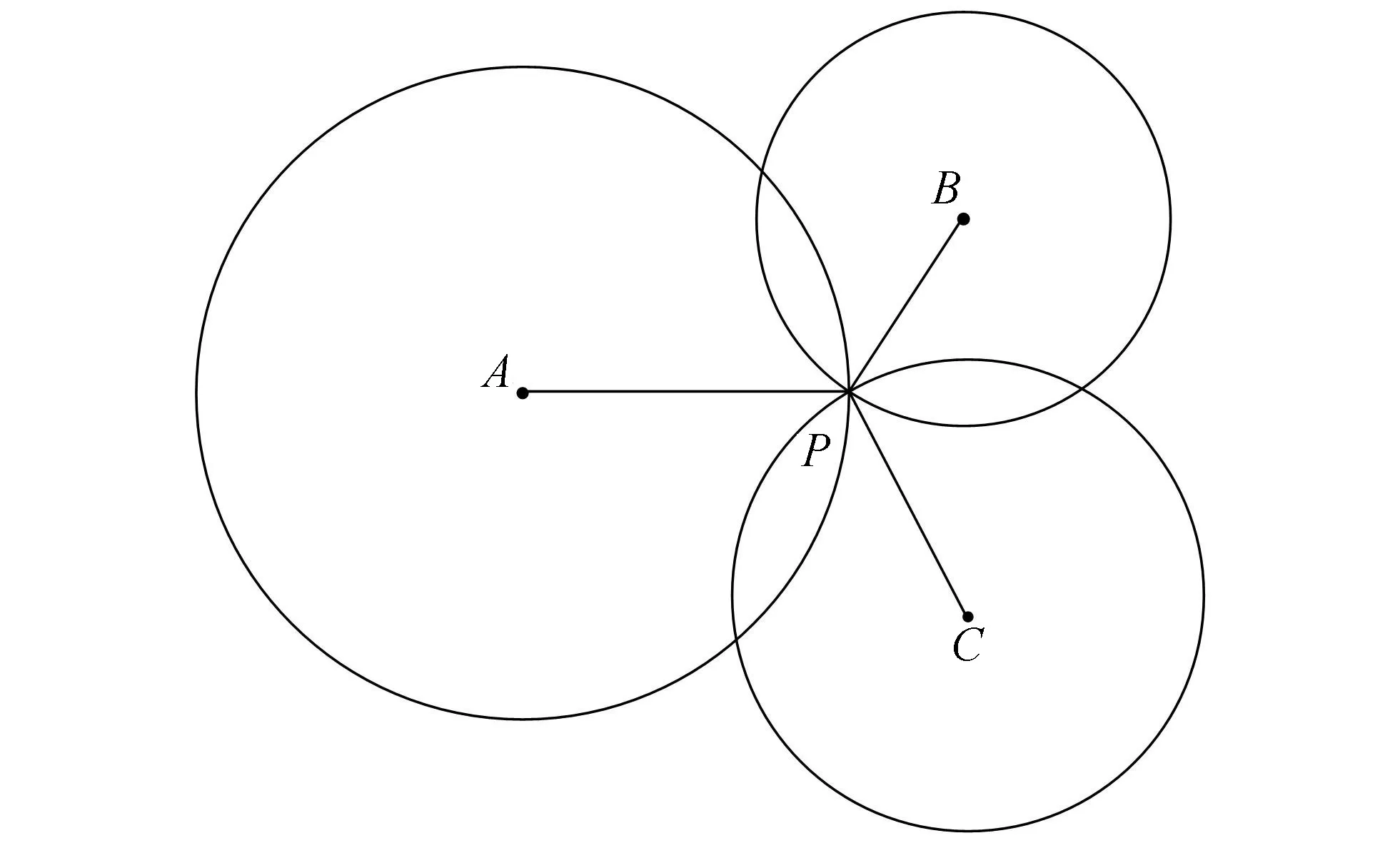
图1 三点定位法示意图

由于节点间距离存在误差，3个圆并不会恰好相交于一点，即求得的LU节点的坐标并不太准确，因此利用三点定位法只能对部分LU节点进行粗略的定位。

当待求LU节点最大测距范围内只有1～2个LA节点时，将距其最近的LA节点的位置作为该LU节点的位置；当待求LU节点最大测距范围内无LA节点时，将区域中心的位置作为该LU节点的位置。

为了满足对于定位准确性的要求，在完成对所有LU节点粗略的初步定位后，需将本次定位结果作为初始值进行下一步的迭代运算。

2.2 迭代优化

求解无约束的优化问题，修正牛顿法是最有效的算法之一。首先，把原目标函数(16)改写为：

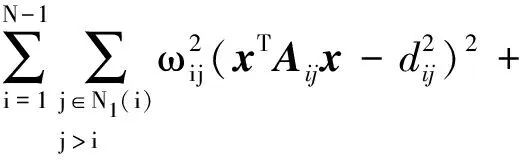
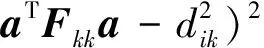
(20)

于是，可得到其梯度向量和Hessian矩阵为：

(21)

4(xTBiix-xTCika-aTDkix+

(22)

(23)

采用的修正牛顿法算法流程为：

1) 以三点定位得到的粗略定位结果作为初始值x0，k=0。

2) 计算步径Δxk=-2f(xk)-1f(xk)和减量fT(xk)2f(xk)-1f(xk)。

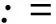
5) 更新xk+1=xk+μΔxk，令k=k+1，返回步骤2)。

考虑到修正牛顿法对初始值的依赖性较大[13]，当选取的初始值x0不合适时，将会影响迭代收敛的速度，甚至不收敛，因此采用三点定位法对LU节点的初步定位结果作为迭代的初始值。同时，若第k个迭代点xk处的Hessian矩阵非正定时，目标函数在xk处的搜索方向Δxk就未必是下降的。所以，对Hessian矩阵进行了修正，以保证其充分的正定性，确保随着迭代的进行，目标函数的值单调下降，从而使得修正牛顿法能够快速收敛[15]。

3 仿真结果及分析

为了评价定位的准确性，采用与文献[8]相同的评价指标：根均方距离(RMSD)。仿真实验主要参数如表1所示。同时，为了更加详细地描述实验过程中定位误差的分布情况，根据重构误差(MRE)绘制了箱形图[11]。

(24)

(25)

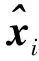
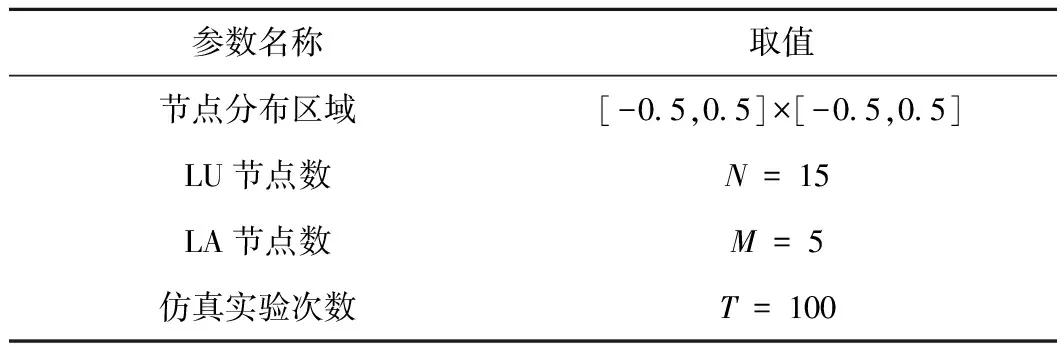
表1 仿真实验主要参数

例1为选取比较合理的LA节点分布，在噪声强度为τ=0.20下，对不同的最大测距范围dmax做仿真实验。图2为4种LA节点分布图，(a)、(b)、(c)、(d)中LA节点的分布依次为：LA=r×[1,-1,0,1,-1;1,1,0,-1,-1],r=0.2,0.3,0.4和LA=rand(2,M)-0.5，三角形表示LA节点，圆圈表示LU节点。图3的散点图是100次仿真实验所得的平均RMSD，其中方形、菱形、圆形、上三角形分别表示LA节点分布(a)、(b)、(c)、(d)的仿真结果，可以看出节点分布(b)的平均RMSD最小；图4箱形图是100次仿真实验所得MRE的分布情况，其中每组箱形图分别表示LA节点分布(a)、(b)、(c)、(d)仿真结果。显然LA节点分布(b)、(c)的MRE是最稳定的，异常值比较少、比较小，且LA节点分布(b)盒形图的中位线最低。综合考虑，LA节点分布(b)定位更为合理，确保了更多的LU节点周围至少有3个LA节点，且更有利于对边缘位置的LU节点进行初步的定位。

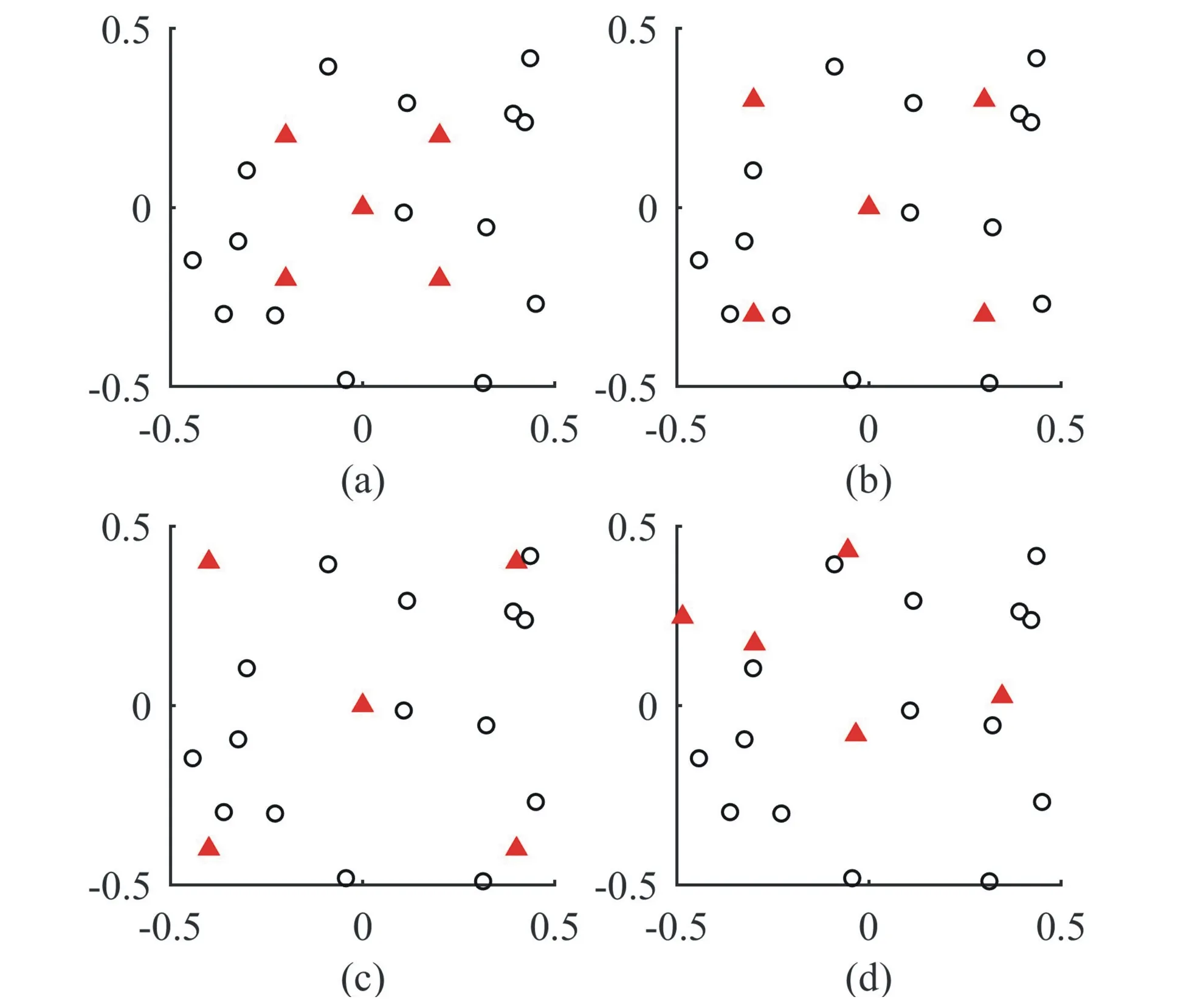
图2 LA节点分布图

图3 100次仿真实验的平均RMSD

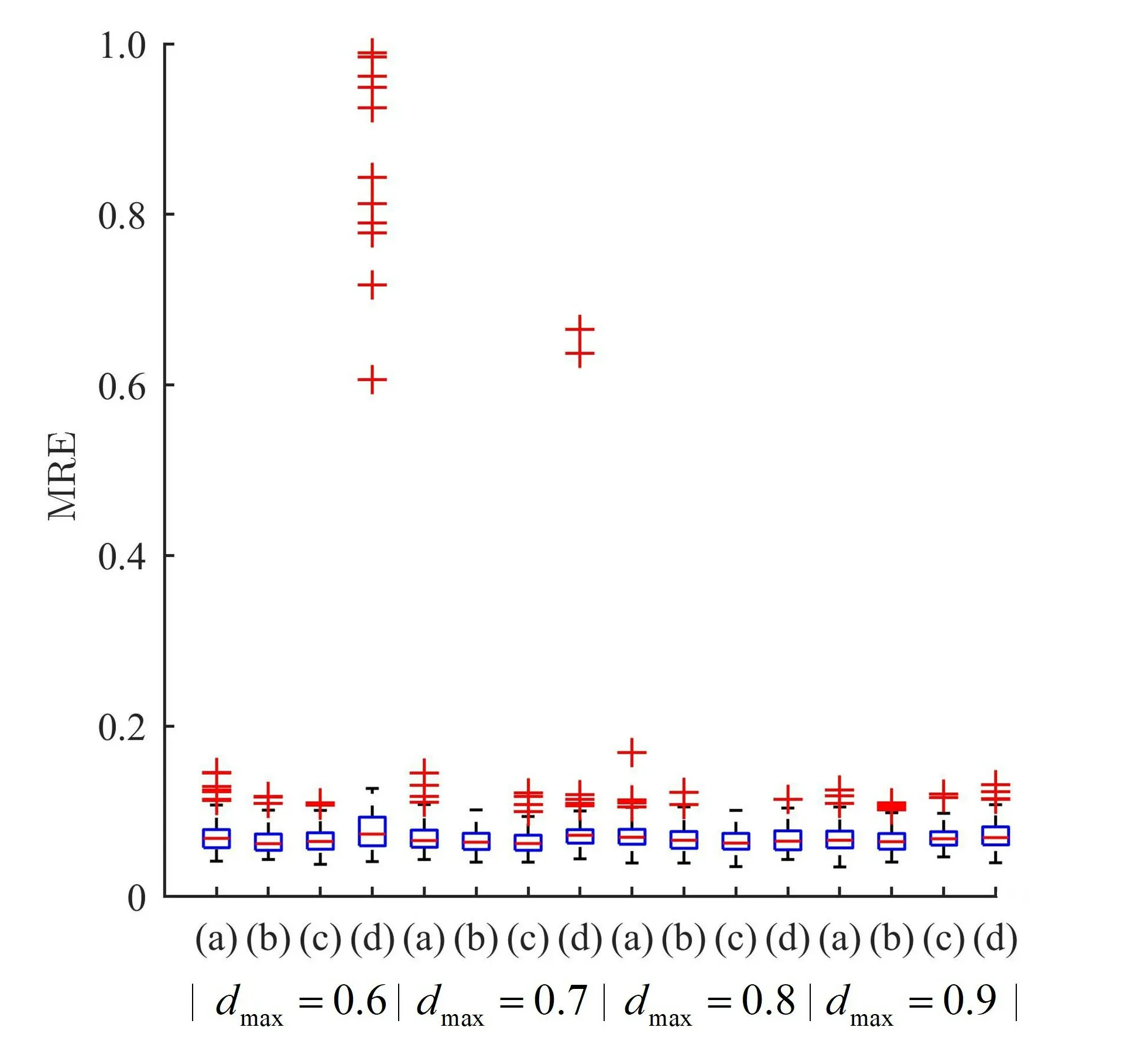
图4 100次仿真实验的MRE分布情况

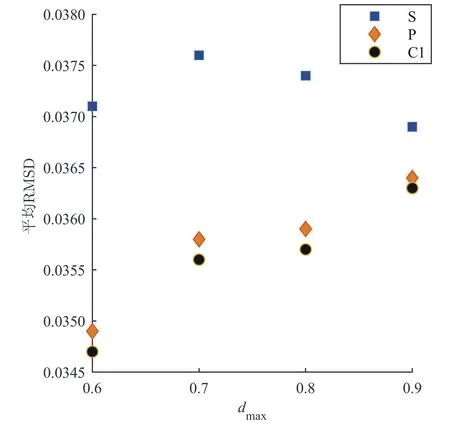
图5 100次仿真实验的平均RMSD

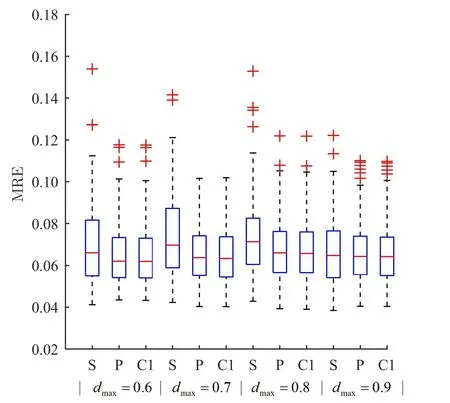
图6 100次仿真实验的MRE分布情况

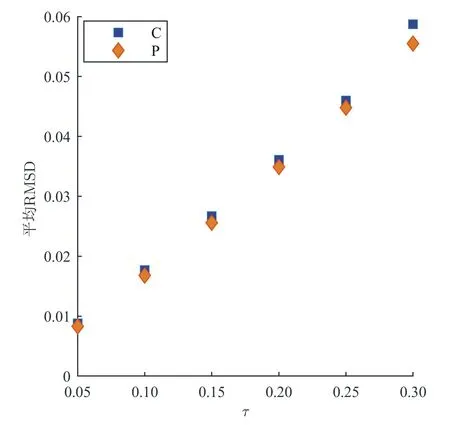
图7 100次仿真实验的平均RMSD

例2为验证本方法初始值x0的选取是否可行，本次仿真对LA节点分布(b)在相同噪声强度τ=0.20和不同的最大测距范围dmax下进行了对比实验。图5的散点图是100次仿真实验所得的平均RMSD，其中方形、菱形和圆形分别表示以随机点、本方法和LU节点真实位置为初始值x0的仿真结果。从图5可看出，本方法选取的初始值x0比以随机点为初始值x0时所得的平均RMSD小，且与以LU节点真实位置为初始值x0时的平均RMSD相近。图6箱形图是100次仿真实验所得MRE的分布情况，其中每组箱形图分别表示以随机点、本方法和LU节点真实位置为初始值x0的仿真结果。从图6可看出，本方法选取的初始值x0和以LU节点真实位置为初始位置x0的MRE最稳定，异常值较少、较小，且箱形图的中位线也最低。因此，本方法选取的初始位置x0是可行的。同时，最大测距半径dmax越小，传感器节点功耗越小，测距数据也越可靠，因此取dmax=0.6较为合理。

例3为了客观地评价本方法的定位性能，本次仿真在相同的LA节点分布(b)，dmax=0.6和不同的噪声强度τ下进行了对比实验。其中，噪声强度τ越大表示测距误差越大。图7的散点图是100次仿真实验所得的平均RMSD，其中菱形和方形分别表示本方法和文献[8]的仿真结果。从图7可看出，噪声强度τ较小时，两者得到的平均RMSD很接近，但当噪声强度τ较大时，本方法所得RMSD明显更小。图8箱形图是100次仿真实验所得MRE的分布情况，其中每组箱形图分别表示本方法和文献[8]方法的仿真结果。从图8可看出，噪声强度τ较小时，两者盒箱形图很相似，但当噪声强度τ较大时，本方法的盒形图中位线更低，异常值更少、更小。表2和表3分别是100次仿真实验的算法平均迭代次数和运行时间，表中数据显示该算法平均迭代次数远小于文献[8]，且运行时间更短。综上，与文献[8]相比，在不同程度的测距误差下，本节点定位方法定位更快、更准确。

图8 100次仿真实验的MRE分布情况

表2 例3中100次仿真实验的算法平均迭代次数

表3 例3中100次仿真实验的运行时间 s

4 结束语

针对WSN中节点间测距误差导致节点定位不准确的问题，提出了一种基于图模型的节点定位方法，并将定位问题归结为一个无约束的凸优化问题。对于该定位问题的求解，首先采用了三点定位方法进行粗略定位，然后采用修正牛顿法进行迭代优化。仿真实验表明，与现有方法相比，本算法在不同程度的测距误差下定位更快、更准确。后续工作将把更多图模型的理论和方法应用到节点定位中，克服对节点位置初始值的依赖和对最大测距范围的局限性，并对大规模WSN中的节点进行定位。