基于Lorenz映射和Logistic映射的图像分块加密算法
陈 军, 张向利, 张红梅
(桂林电子科技大学 认知无线电与信息处理省部共建教育部重点实验室,广西 桂林 541004)
随着网络和数字多媒体技术的飞速发展,人们的生活方式有了很大变化。数字图像能形象地表达人们的所思所想,因此数字图像成为了人们进行日常沟通交流的主要方式之一。由于网络开放共享的特点,数字图像在存储和传输中很容易受到人为攻击,而图像加密就是保障图像信息安全的主要方式。
图像具有数据量大、相关性强、冗余度高、能量分布分散等特性。随着计算机容量和存储的不断升级以及密码分析的发展进步,一些传统加密算法的缺点开始逐渐显现出来[1]。传统的加密算法若用于图像加密,会导致计算量大,效率低下,很难保证实时性的需求。混沌系统具有的伪随机性、初值敏感性和遍历性等动力学特性使得混沌十分适合运用到图像加密之中。近年来,有很多混沌映射用于图像加密的算法产生。文献[2]提出了一种利用分段非线性Logistic构造灰度置乱对图像进行加密的算法,该算法较传统算法运算速度更快,但安全性不足。文献[3]设计了一种采用高维混沌映射来进行位置置乱的图像加密算法,该算法有着较强的密钥敏感度和较大的密钥空间,但该算法未改变图像像素灰度值,无法抵御差分攻击。
随着研究的不断深入,逐渐出现了一些性能较好的图像加密算法。赵玉青[4]设计了一种基于改进的Chen超混沌系统的图像加密算法,该算法引入时间延迟用以改善混沌序列,其次用改善后的超混沌序列对图像进行置乱,以达到加密图像的目的。该算法密钥空间大、敏感性高,但加密过程比较繁琐。房东鑫等[5]提出了一种基于广义Arnold映射和DNA编码的图像加密算法,该算法采用Arnold映射对图像进行置乱,利用DNA编码碱基对互补替换进行图像像素灰度值扩散得到加密图像。但低维混沌映射存在周期窗口问题,给加密安全性带来了隐患。徐亚等[6]设计了一种基于Arnold映射的分块扩散图像加密算法,该算法采用多种一维混沌映射的组合生成混沌序列,定义与明文等大小的矩阵进行分块并记录操作,同时进行块内和块间的扩散。该算法敏感性高,加密效果良好,但算法复杂度较高,加密速度较慢。
既要避免低维混沌映射存在周期性窗口和安全性较低的问题,又要保证一定的加密效率。为此,研究了一种基于三维Lorenz映射和Logistic映射的图像分块加密算法。在传统以置乱扩散为主体的加密算法的基础上,优化改进了具体细节操作。首先,对明文图像进行置乱操作;其次,对置乱后的图像进行分块,然后依次对图像进行块内扩散操作和块间扩散操作,最终得到加密后的密文图像。为了有效地抵御选择明文攻击,利用明文图像的哈希值对混沌映射的初值和参数进行处理,使得每次加密时的初值和参数随明文自动发生变化。
1 算法基础
1.1 Lorenz 混沌映射
Lorenz映射是三维连续混沌映射,其数学表达式的描述形式是微分方程。它是气象学家Lorenz在1963年研究气象学时发现的,其映射表达式如式(1)所示:
(1)
其中,σ、r、c为Lorenz映射的控制参数,一般取值为σ=10,r=28,c=8/3。在σ,c不改变的条件下,当r>24.74时,Lorenz映射开始进入混沌状态。
1.2 Logistic 混沌映射
Logistic映射是美国数学生态学家R.May于1976年提出的。由于是研究昆虫群体繁殖规律时发现的,因此又被称为“虫口模型”[7]。Logistic映射最初用来研究昆虫的个体数量和环境间关系。它的形式虽然简单,却蕴含着复杂的动力学行为。其数学表达式为:
xn+1=μxn(1-xn)。
(2)
其中:xn∈(0,1);n=0,1,,n;μ∈(0,4],μ为系统的控制参数,当μ取不同值时,式(2)会显现出不同的状态,当3.569 945 6≤μ≤4时,系统开始进入混沌状态。
2 加密算法设计
2.1 密钥的生成
采用了一种利用明文图像的哈希值对混沌映射的初值和参数进行处理得到加密密钥的方法,使得每次加密时的密钥可自动发生变化。
哈希函数可以将任意长度的数据映射到固定长度的域上,即输入可变长,输出为固定长。在密码学中,哈希函数早已有广泛应用,经典的哈希算法有SHA-2、MD5等。两幅图像即使只有一个比特不同,它们的哈希值也完全不同[8]。
图像加密之前首先选取哈希算法,选择SHA-2算法,计算明文图像的哈希值Pv,Pv的长度为256位,将它划分为8组,每组包括8个16进制数,即pk1pk2pk7pk8,k=1,2,,8。对于每一组而言,采用式(3)将其变换为10进制浮点数dk,dk∈(0,0.1)。
dk=hex2dec(pk1pk2pk7pk8)×10-12
(3)

(4)

(5)
通过以上方式,确保密钥的生成依赖于明文,每次加密时密钥能够自动发生变化,而无需修改初始值[8]。
2.2 加密算法流程
加密算法流程图如图1所示,算法主要包括混沌序列的产生,图像的置乱、分块和扩散等步骤。首先,通过密钥的生成方法对Logistic映射和Lorenz映射的初始值和参数进行处理得到密钥。采用Logistic映射对明文图像进行位置置乱,其次对置乱后的图像进行分块,然后利用Lorenz混沌映射生成的序列对分块后的图像分别进行块内扩散和块间扩散操作,使每个像素尽可能多地分散到整幅图像中,完成加密过程。

图1 加密流程图
加密的主要步骤:
1)读取一幅大小为M×N的灰度图像I,采用Logistic映射生成一组混沌序列,去掉前δ1,得到长度为MN序列X(k),将序列X(k)按式(6)处理得到新的序列X(k),其中floor函数是向下取整函数,使用新的序列X(k)对图像进行像素点的置乱得到置乱后的图像I1。
floor(x(i)×1010)modMN。
(6)
2)对图像I1进行分块,划分成大小为t×t的子块(t是M、N的公约数)。
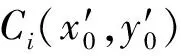
ci(x′,y′)=
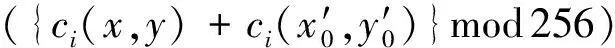
(7)

⊕S(k)。
(8)
2.3 解密过程
解密过程和加密过程正好相反,是加密过程的逆操作,主要步骤如下:

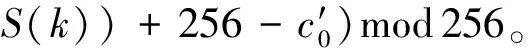
(9)
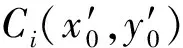
ci(x,y)=

(10)
3)进行逆置乱操作,即得到最后的明文图像。
3 实验结果
实验仿真软件选择的是MATLAB R2014a,图像则选取了大小为256×256的灰度图像Lena和Baboon。加密的初始密钥为Lorenz映射和Logistic映射的初始值和参数,其中σ=10,r=28,c=8/3,x0=1.000 1,y0=1.300 2,z0=1.200 3,x1=0.256 7,μ=3.816 2,δ1=δ2=δ3=200。原图像和加密图像如图2所示。观察密文图像,从图像中看不出原始图像的信息,表示该算法加密效果良好,达到了隐藏原始图像信息的目的。
4 安全性分析
4.1 密钥空间分析
密钥空间指的是密钥的取值范围。为了确保图像加密算法的安全性,密钥空间应该大到能够防止穷举等暴力攻击。Alvarez等[9]建议,加密系统的密钥空间至少达到2100,才算是足够安全。在一定程度上,密钥空间越大越好。
加密算法实际用到的初始密钥主要来自Lorenz映射和Logistic映射的初始值和参数,主要包括:x0,y0,z0,x1,μ,由于这些值都是双精度实数,最大精度可取到10-15,因为Logistic映射的参数值μ∈(3.6,4],故Logistic映射参数值的密钥空间为0.5×1015,加密算法总的密钥空间为:0.5×1015×1015×1015×1015×1015≈5×1074≫2100,因此,该加密算法的密钥空间比较大,足够抵御穷举等暴力攻击。除此之外,图像的置乱次数,图像分块的分块大小,块内扩散次数和块间扩散次数等等都是密钥的一部分,此处并未列入。
4.2 密钥敏感性分析
好的图像加密算法应对密钥的变化足够敏感,即使密钥发生很小的改变,也无法正确地还原出原始明文图像。如图3所示,以Lena灰度图像为例,图3(a)是使用原始密钥进行解密得到的图像,即正确解密恢复的原始明文图像。图3(b)、(c)是Logistic映射的初始值和参数改变量=10-15时进行解密得到的图像,与原始明文图像完全不同。从图3可看出,当密钥的改变量只有=10-15时,图像依然无法正确地完成解密。可见即使密钥只有微小的变动,解密后的图像与原图像却千差万别,表明该算法有较好的密钥敏感性。

图2 明文图像和密文图像
4.3 直方图分析
图像灰度直方图是图像中像素的分布密度图,是图像最基本的统计特征,可以依据密文图像的直方图来衡量图像加密算法的性能,一个均匀、平滑的直方图可以抵御直方图的统计攻击。以Lena图像为例,图像加密前后的直方图如图4所示。通过观察加密前后的灰度直方图能够发现,原始明文图像中,许多像素点的灰度值集中在少数几个灰度值附近,而加密后的灰度直方图显示,像素灰度值分布相对均匀,无明显突出灰度值的存在。这表示该加密算法加密效果较好,很难依靠直方图攻击来完成破解。
4.4 相关性分析
相邻像素的相关性描述的是图像相邻像素灰度值的关联程度,相关系数值越小,则表示相邻像素越没有关系,相关系数值越小,越能抵御统计分析攻击,越能拥有好的加密效果。在正常情况下,依照图像信息的特点,原始明文图像相邻像素间的关联性很强,而有效的图像加密算法应该设法削弱原始待加密图像中相邻像素间的相关性。相关系数的公式如下:
(11)
(12)
(13)
(14)
其中:x,y为像素的灰度值;rxy为相关系数;cov(x,y)为协方差;E(x)为均值;D(x)为方差。通常密文图像的相邻像素的相关系数值越接近于0,加密效果越好。以Lena图像为例,随机选取原始明文图像和加密后密文图像中各2 000对相邻像素,计算其水平、竖直和对角3个方向的相邻像素值,结果如表1所示。
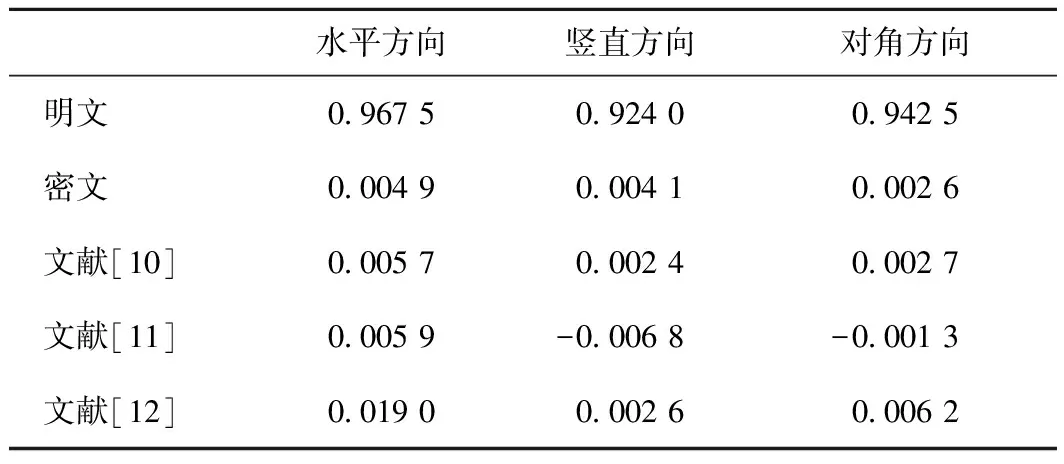
表1 明文图像和密文图像的相关系数
从表1可见,明文图像的相关系数非常大,趋近于1,而密文图像中相邻像素间的相关系数已经趋近于0。与所列的文献相比,比文献[12]、[13]效果要好,与文献[11]效果相当,达到了不错的加密效果。
4.5 信息熵分析
信息熵可以衡量图像灰度值的分布信息,其值越大,图像的随机性越好。对于密文图像而言,信息熵越大,随机性越好,加密效果越好。设信息源为m,则信息熵为
(15)
其中p(mi)为信息m出现的概率。对于256灰度级的密文图像,其信息熵的值越接近8,则表示图像的加密效果越好。分别计算Lena图像和Baboon图像的信息熵,结果如表2所示。从表2可看出,加密后图像的信息熵已经接近于8,比所列文献的效果要好。
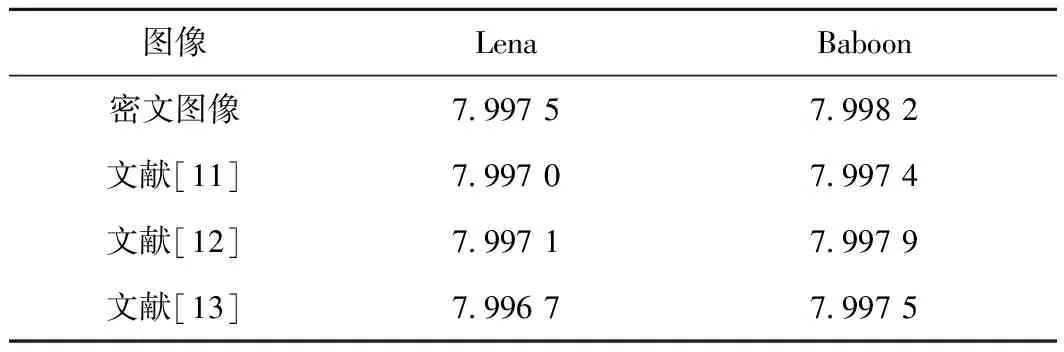
表2 密文图像的信息熵
5 结束语
为了解决低维混沌映射密钥空间小,安全性能不高的问题。提出了一种基于Lorenz映射和Logistic映射的图像分块加密算法。首先,采用Logistic映射对明文图像进行置乱操作;其次,对置乱后的图像采取分块处理,接着根据Lorenz映射生成的混沌序列分别对图像进行块内扩散操作和块间扩散操作,最终得到加密后的密文图像。仿真实验结果表明:该算法密钥空间大,密钥敏感性强;密文图像灰度直方图分布均匀,相邻像素的相关性弱,具有较好的加密性能。

