基于CACC的译码转发协作方式的中断概率分析
张秋玉, 肖海林,2, 蒋 为, 邱 斌,3, 倪 菊
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.温州大学 物理与电子信息工程学院,浙江 温州 325035;3.桂林理工大学 信息科学与工程学院,广西 桂林 541004;4.桂林电子科技大学 图书馆,广西 桂林 541004)
协同自适应巡航控制(cooperative adaptive cruise control,简称CACC)系统[1-2]是指装配自适应巡航控制系统的汽车通过车辆与车辆(vehicle-to-vehicle,简称V2V)或路侧单元与车辆(roadside-to-vehicle,简称R2V)利用无线设施相连接组成的车辆跟随控制系统。该系统通过界定车辆间信息传输的中断概率阈值,使得车辆之间信息传输中断概率稳定并保证车辆安全行驶。现在绝大多数CACC系统均采用车载雷达作为车载传感器,根据雷达传感器感知前方环境,如车间距和相对速度,还可以通过无线通信获得前方车辆和其他相关车辆的信息,如车辆的速度、预期加速度,使彼此“相连”的车辆协同完成操控[3-4]。
CACC系统普遍利用车辆间的无线通信来提高系统的性能,以提供额外的信息增加距离传感器数据,并且在信息传输过程中,通信协作方式经常被用来获得更好的信息传输系统性能[5-8]。译码转发(decode-and-forward,简称DF)协作方式会影响通信系统的中断概率性能。文献[5]分析了在最优中继选择的情况下,DF协作方式对中断概率性能的影响。文献[6]考虑到信道状态信息的不完全性,并分析了DF协作方式对通信中断概率的影响。文献[7]给出了在Nakagami-m信道状态下,利用DF方式所得到的中断概率的确切表达式和渐进表达式。文献[8]分析了在受到噪声干扰的情况下,运用DF协作方式对系统中断概率的影响。这些只考虑静态条件下DF协作方式对中断概率产生的影响,未考虑车辆行驶过程中前后车辆之间距离的变化对CACC系统信息传输性能的影响。
为此,基于CACC系统建立实时距离变化反映时变特性的车辆行驶队列模型,运用DF协作转发方式优化时变距离下系统的信道容量[9]及中断概率。
1 协同自适应巡航控制系统车队模型
车辆行驶队列模型如图1所示。设xs、xr分别为源节点车辆s和中继节点车辆r发出的信息,ys-d、yd为目的节点车辆d收到的信号,ys-r为中继节点车辆r收到的信号,n0为方差为σ2的加性高斯白噪声。假设该自适应巡航车队列中有m辆车,di=qi-1-qi为车辆i与车辆i-1两车之间的距离,其中qi、qi-1分别为两车后保险杠位置,vi为车辆i的速度。

图1 车辆行驶队列模型
CACC的目的是让每辆车以期望的距离dg跟随其前一辆车,并采用间隔策略[10-12]:
dg,i(t)=dt,i+hvi(t),i∈m。
(1)
其中:dg,i为车辆i与车辆i-1两车之间的期望距离;h为采样时间间隔;dt,i为停止距离。
由期望距离dg,i及间隔策略可得到自适应巡航控制系统中两车之间的距离误差为
ei(t)=di(t)-dg,i(t),i∈m。
(2)
只有当首车加速度a1=0,且前后车辆等速行驶时,两车之间的距离误差ei(t)才可以保持稳定。于是,拟定以下输入控制量来保持两车距离:
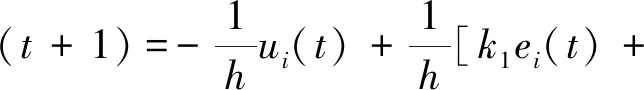
(3)
其中k1、k2和k3为控制器系数,即与控制系统性能有关的常数,取k1=0.2,k2=0.7,k3=0。将车辆i的状态定义为
(4)
假设在t时刻第i-1车向第i+1车发送信息,第i车作为中继节点车辆,则第i+1车的状态为:
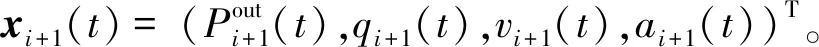
(5)
第i+1车的状态信息中t+1时刻的加速度可根据t时刻的加速度推导:
ai+1(t+1)=e-h/ηai+1(t)+(-e-h/η+1)ui+1(t),
(6)
η为标准采样间隔。根据t时刻的加速度及速度推导出t+1时刻的速度为
vi+1(t+1)=vi+1(t)+(-ηeh/η+η)ai+1(t)+
[η(e-h/η-1)+h]ui+1(t)。
(7)
根据t时刻的距离、速度及加速度推导出第i+1车t+1时刻的后保险杠位置为
qi+1(t+1)=qi+1(t)+hvi+1(t)+
[η(e-h/η+1)+h(-η+h)]ui+1(t)+
(η2e-h/η+ηh-η2)ai+1(k)。
(8)
在t+1时刻,源节点s、中继节点r及目的节点d三者之间的距离为:
ds-d(t+1)=qi-1(t+1)-qi+1(t+1),
(9)
ds-r(t+1)=qi-1(t+1)-qi(t+1),
(10)
dr-d(t+1)=qi(t+1)-qi+1(t+1)。
(11)
通过上述对车辆状态空间的描述,可以得到相应的车辆的运动状态:
xi(t+1)=Axi(t)+Bui(t),
(12)
yi(t)=Cxi(t)。
(13)

2 协作通信传输协议
信息协作通信基本模型如图2所示。hs-d、hs-r、hr-d表示平坦衰落信道下的信道增益,ds-d、ds-r、dr-d分别表示源节点s与目的节点d、源节点s与中继节点r、中继节点r与目的节点d的距离,α表示路径损耗指数,b表示数据传输速率,ps、pr分别表示源节点车辆和中继节点车辆的功率[13]。

图2 信息协作通信基本模型
2.1 直接传输(DT)
目的节点通过信道收到源节点发送的信息为
(14)
t时刻源节点s与目的节点d之间的信道容量为
(15)
中断概率可表示为
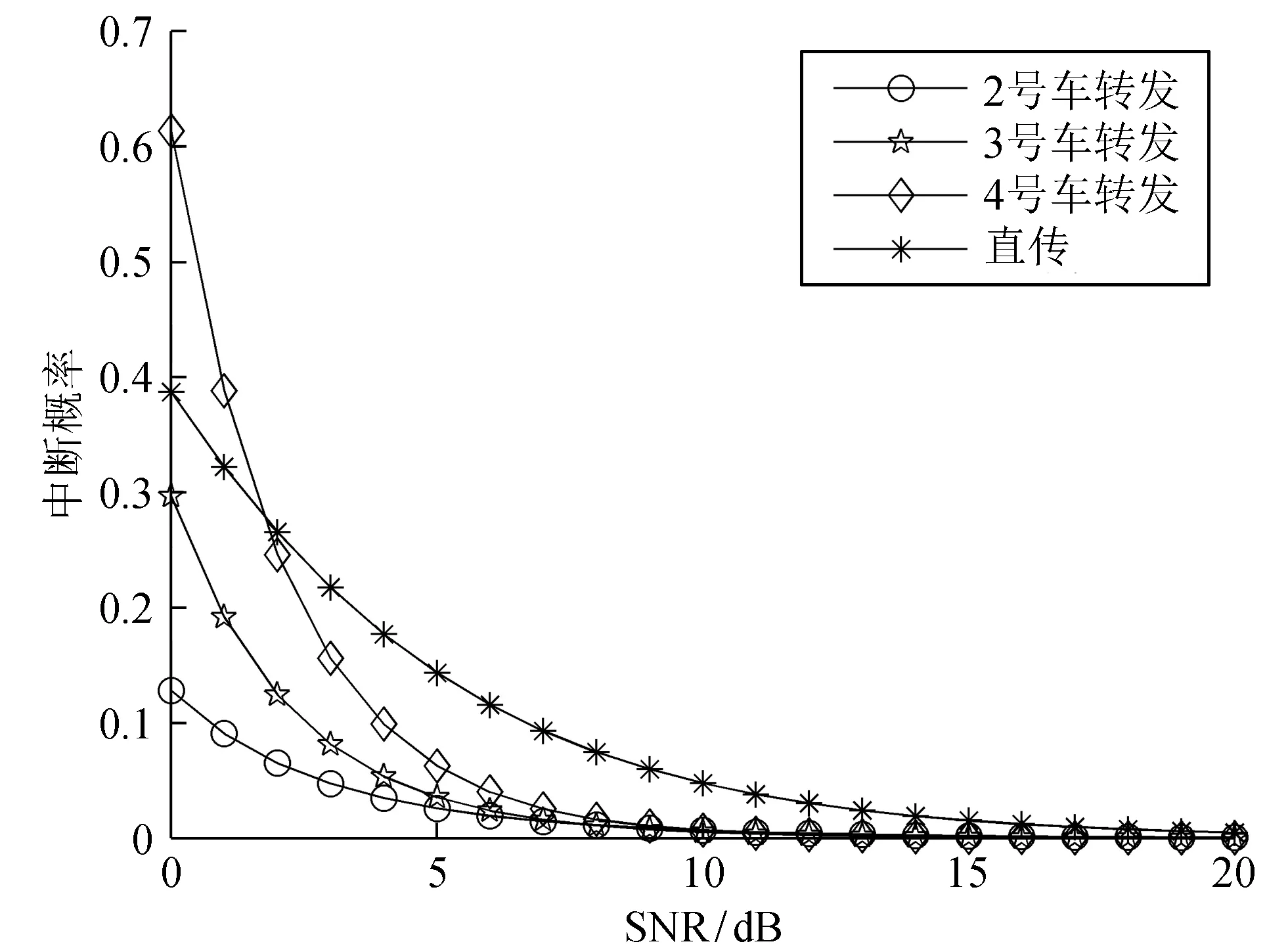
Pout(t)=P[Is-d(t) (16) 其中:P[·]表示求概率;p0为归一化功率。 译码转发分为2个时隙。第1时隙,源节点发出信号xs,中继节点和目的节点接收到的信息为: (17) 第2时隙,目的节点接收到的信息为: (18) 其中f(ps)=(22b-1)/ps。在译码转发的方式下,仅当信噪比(SNR)超过门限值时,中继节点才会进行信息的转发,否则源节点在第2时隙重新发送信息。 若接收到的SNR超过门限值,中继节点r可以进行完美解码,则这种信息转发方式下的信道链路容量为: (19) 因此,中断概率可表示为[8] (20) 由此可得到源节点车辆与目的节点车辆之间的中断概率为 (21) 为分析具有时变特性的车队中利用不同车辆进行信息转发时对车辆间的通信产生的影响,假设该车队列有5辆车,从右至左的车辆依次编号为1~5。在平稳跟车的行驶状态下,相邻两车的间距保持为均值35 m,方差σ2=5的高斯分布,即5辆车的相互间距的取值范围为(30,40)。设噪声信号N0的功率为1,p为源节点发射信号的功率与噪声信号功率的比值,可将p看作源节点的信噪比,损失因子α取2。 图3为车队列中不同中继车辆进行译码转发与直传方式下对车辆通信中断概率产生影响的关系曲线。从图3可看出,信息传输的中断概率随着信噪比的增大有很明显的下降趋势。当信噪比较低(小于2 dB),无论采用何种方式或哪一辆车进行转发,中断概率均在10%以上,都无法达到较为理想的效果。在信噪比为2~18 dB,增大信噪比能降低中断概率。由图3可知,使用离源节点较近的车辆进行信息转发时,中断概率的表现会优于靠后的车辆,即在信息转发过程中,第一时刻的信息转发和传输距离对目的车辆的中断概率存在有较大的影响。当信噪比大于2 dB,车队列中的中继车辆采用译码转发方式的中断概率一直低于其采用直传方式的中断概率。 图3 车辆2种通信方式的中断概率 图4为2号车辆进行译码转发与直传在不同的信息传输速率和信噪比下中断概率。从图4可看出,在信噪比较低且信息传输速率较大的情况下,无论采用何种协作方式进行车辆间的信息传输,都无法取得良好的效果。由图4可知,在较低信噪比(0~2 dB)、较高信息传输速率(1.08~1.20 bit/s)下,直传方式优于译码转发方式。信噪比的增大,信息传输速率不会对中断概率产生较大的影响。当信噪比增大至8 dB,译码转发方式的信息传输中断概率比直传方式约低8.7%。 图4 2号车辆进行译码转发与直传在不同信息传输速率与信噪比下中断概率 图5为源车辆与目的车辆进行信息传输时,随机选用中间车辆进行信息转发所得到的平均中断概率。假设对中间车辆随机选取10 000次进行信息的协助转发,将所得到的中断概率取得平均值。从图5可看出:在信息传输速率较低(0.8~0.9 bit/s)的情况下,信噪比的增大对中断概率的影响不是很明显;当信息传输速率较高,信噪比为0~8 dB的中断概率有十分明显的降低,约从0.66减小到0.09;而当信噪比继续增大,中断概率的提高不明显。因此,在车辆进行信息传输时,为使信息传输的效率更高,即在较大的信息传输速率的情况下,将信噪比保持在8~10 dB即可取得良好的中断概率性能。 图5 随机选取中间车辆进行信息转发的中断概率 基于CACC建立了实时距离变化反映时变特性的车辆行驶队列模型,给出了直传方式与DF车载协作方式下中断性能的计算表达式,分析了时变距离特性对中断概率表达式的影响。实验结果表明,在较理想的信噪比条件下,使用译码转发的中断概率明显小于直传方式。采用离源节点较近的车辆进行信息转发,能降低车辆行驶队列目的车辆节点的中断概率。适当降低信息传输速率,可降低系统的中断概率,为实现车辆行驶队列中的安全通信提供良好的参考。2.2 译码转发(DF)
3 数值结果与分析


4 结束语

