基于动态时间规整的模型传递方法

王文颢， 刘振丙， 雒志超

(1.桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004；2.桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004)

由于近红外技术的非接触、速度快等特点，被广泛使用在农产品[1]、食品[2]和药物[3]的质量检测。近红外光谱定量分析法[4]利用已知的样本及性质通过化学计量学方法可建立定量分析模型，用于未知样本的性质预测。

在应用中，由于源机与目标机的测量光谱存在偏差，所以不能直接使用源机上建立的定量分析模型。若在目标机上再次测量多组样本数据，建立新的定量分析模型又费时费力。为了解决这一问题，模型传递技术[5]应运而生。模型传递技术首先建立源机的测量光谱与目标机的测量光谱间关系的数学模型，再通过该模型对目标机上的光谱进行转换。用在源机建立的定量分析模型，分析传递后的光谱便可获得更准确的预测结果。

模型传递分为有标样法和无标样法。有标样法需要使用标准样本在多机上分别检测，而无标样法不需要标样集。有标样方法包括Shenk’s算法[6]、直接校正法(DS)[7]、分段校正法(PDS)[8]等；无标样方法包括有限脉冲响应算法(FIR)[9]。其中直接校正法和分段校正法是主流的模型传递方法。直接校正法直接使用源机和目标机上测量光谱整体来构建校正模型；分段校正法法是直接校正法的改进，增加了源机光谱波长点和目标机光谱波长点近邻的限制窗口，窗口的大小直接影响校正的结果。

动态时间规整算法(dynamic time warping,简称 DTW)[10-11]在语音分析中经常使用。因为人声的随机性，同一单词的2次发音并不相同，动态时间规整算法可以寻找两组语音序列中帧的关系，计算序列的相似度。

提出的模型传递算法基于动态时间规整算法。该算法首先计算双机光谱上波长点的相关距离。再使用动态时间规整算法寻找使整体的相关距离最小的源机光谱与目标机光谱的关联关系。最后根据关联关系，构建回归模型。

1 算法描述

设Sm(i,j)为源机的光谱矩阵，Ss(i,j)为目标机的光谱矩阵。其中S(i,:)是第i个光谱样本的波长数据，S(S,j)是每个光谱样本的第j个波长点的吸光度。

1.1 计算波长点的相关距离

近红外光谱设备受到自身老化、环境温湿度等条件的影响，源机与目标机测得的光谱之间不但会产生基线漂移，而且波长点也会产生偏移，故需要建立源机光谱Sm与目标机光谱Ss的对应关系。当源机光谱第p个波长点Sm(:,p)与目标机光谱第q个波长点Ss(:,q)对应时，向量间的相关距离小，则相关系数大。相关系数使用皮尔逊相关系数计算,

(1)

根据相关系数计算相关距离,

DSm(:,p),Ss(:,q)=1-ρSm(:,p),Ss(:,q)。

(2)

1.2 动态时间规整算法

对于给定的2个序列X=(x1,x2,,xN)和Y=(y1,y2,,yM)，使用动态时间规整得到2个序列的匹配关系。当2个序列间的距离最小时，匹配关系是最佳的。两个序列的匹配关系如图1所示。

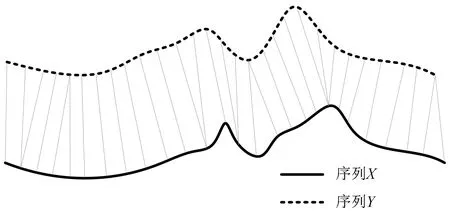
图1 两个序列的匹配关系

光谱数据Sm(:,i)可以看作序列X中xi，Ss(:,j)可以看作序列Y中yi。

1.2.1 计算代价矩阵

首先构造一个代价矩阵C∈RN×M,它由序列中的元素的距离构成。将其元素定义为：

ci,j=Dxi,yj,xi∈X,yj∈Y。

(3)

朴素的动态时间规整算法使用Dxi,yj=‖xi-yj‖作为距离。这里更关注元素的相关性，故

Dxi,yj=1-ρxi,yj。

(4)

1.2.2 计算规整路径

动态时间规整方法可以依据代价矩阵得到一条规整路径。图2为一条从序列X到序列Y的规整路径。

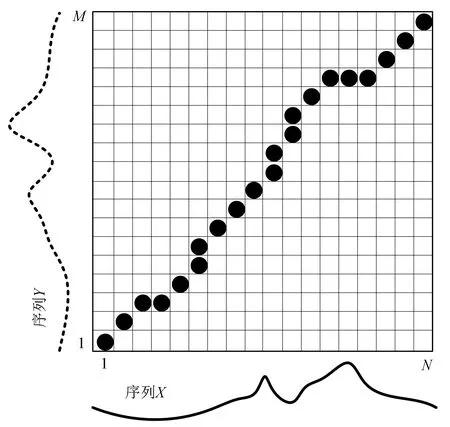
图2 最佳规整路径

设P=(p1,p2,,pL)为规整路径，pl=(xi,yj)为路径中的第l个元素，表示序列X的元素xi和序列Y的元素yj相关。规整路径必须满足3个条件：

1)边界条件。起点只能是(x1,y1)点，终点只能是(xN,yM)点。

2)顺序限制。序列中的点必须依次逐个匹配，禁止跳过序列中的点。

3)步长限制。一次只能移动一步进行匹配，方向为向右、向上、向右上，例如当前点为(xi,yj)，那么下一步只能为(xi+1,yj)、(xi,yj+1)或(xi+1,yj+1)。

使用规整路径的代价和作为算法的损失函数，

(5)

当pl=(xi,yj)时，c(pl)=c(xi,yi)=cxi,yj。动态时间规整算法寻找代价和最小的规则路径：

DTW(X,Y)=min{CP(X,Y)}。

(6)

构造累计代价矩阵Dacc，其计算式为：

当i=1,j=1时，

Dacc(i,j)=c(xi,yj)；

(7)

当i=1,2≤j≤M时，

Dacc(i,j)=Dacc(i,j-1)+c(xi,yj)；

(8)

当2≤i≤N,j=1时，

Dacc(i,j)=Dacc(i-1,j)+c(xi,yj)；

(9)

当2≤i≤N,2≤j≤M时，

Dacc(i,j)=min{Dacc(i-1,j-1),Dacc(i-1,j),

Dacc(i,j-1)}+c(xi,yj)。

(10)

当前点累计的代价是前一步的最小累计代价与当前点代价的和。累计代价矩阵构造完成后，从终点pL=(xN,yM)按最小累计代价回溯到起始点p1=(x1,y1)即可得到规整路径。

1.2.3 根据规整路径建立校正模型

源机与目标机测量光谱的波长点的关系由规整路径确定。根据此关系来构建校正模型。

当Sm(:,i)与Ss(:,j)单一对应时，构造一元回归方程：

Sm(:,i)=bi,M+1+bi,jSs(:,j)。

(11)

当Sm(:,i)与Ss(:,j-n)到Ss(:,j+m)相匹配时，构建多元回归方程：

Sm(:,i)=bi,M+1+bi,j-nSs(:,j-n)++

bi,j+mSs(:,j+m)。

(12)

式(11)、(12)通过最小二乘法求得系数。完成每个波长点的计算后，构造转移矩阵F∈R(M+1)×N，其元素为回归方程的系数，定义为：

(13)

(14)

2 实验部分

2.1 数据集

为验证基于动态时间规整算法的模型传递方法，实验数据使用的药物数据集和玉米数据集来自网页(http://www.eigenvector.com/data/tablets/index.html)和网页(http://www.eigenvector.com/data/Corn/index.html)。

药物数据集来自2台近红外光谱仪对654片药片样本采样获得的数据。每个样本的光谱波长从600～1898 nm，采样间隔2 nm，共650维。采集到的654对光谱数据被分为训练155对、测试460对和验证40对。此外，还包含药物质量、药物硬度、活性物质含量3种性质供分析使用。

玉米数据集是3台近红外光谱仪对80个玉米样本采样获得的数据。每个样本的光谱波长从1100～2498 nm，采样间隔2 nm，共700维。此外，还包含油、水、淀粉和蛋白质含量4种性质供分析使用。

2.2 建立定量模型

对于药物数据集，先对光谱数据做零均值化处理。选择仪器1作为源机，在训练集上使用PLS算法对药物数据创建定量分析模型，对药物的3种性质进行预测。

对于玉米数据集，先对光谱数据做零均值化处理。选择m5作为源机，使用K-S算法划分训练集和测试集。其中训练集样本50个，测试机样本30个。使用PLS算法对训练集创建定量分析模型，对玉米的4种性质进行预测。

使用10折交叉验证创建定量分析模型，最优的PLS模型主因子数由平均预测均方差确定，结果如表1所示。

表1 使用源机光谱建立的PLS模型

2.3 使用动态时间规整算法建立传递模型

使用动态时间规整算法得到规整路径，以此得到波长点的对应关系。

药物数据集以波长600～920 nm为例，对应关系和规整路径如图3、4所示。图3中圆形点为源机波长点，星形点为目标机波长点，二者的细线是其对应关系。可以看出，在700 nm附近的峰值存在变化，动态时间规整算法能找到准确的对应关系和规整路径，并建立回归方程。

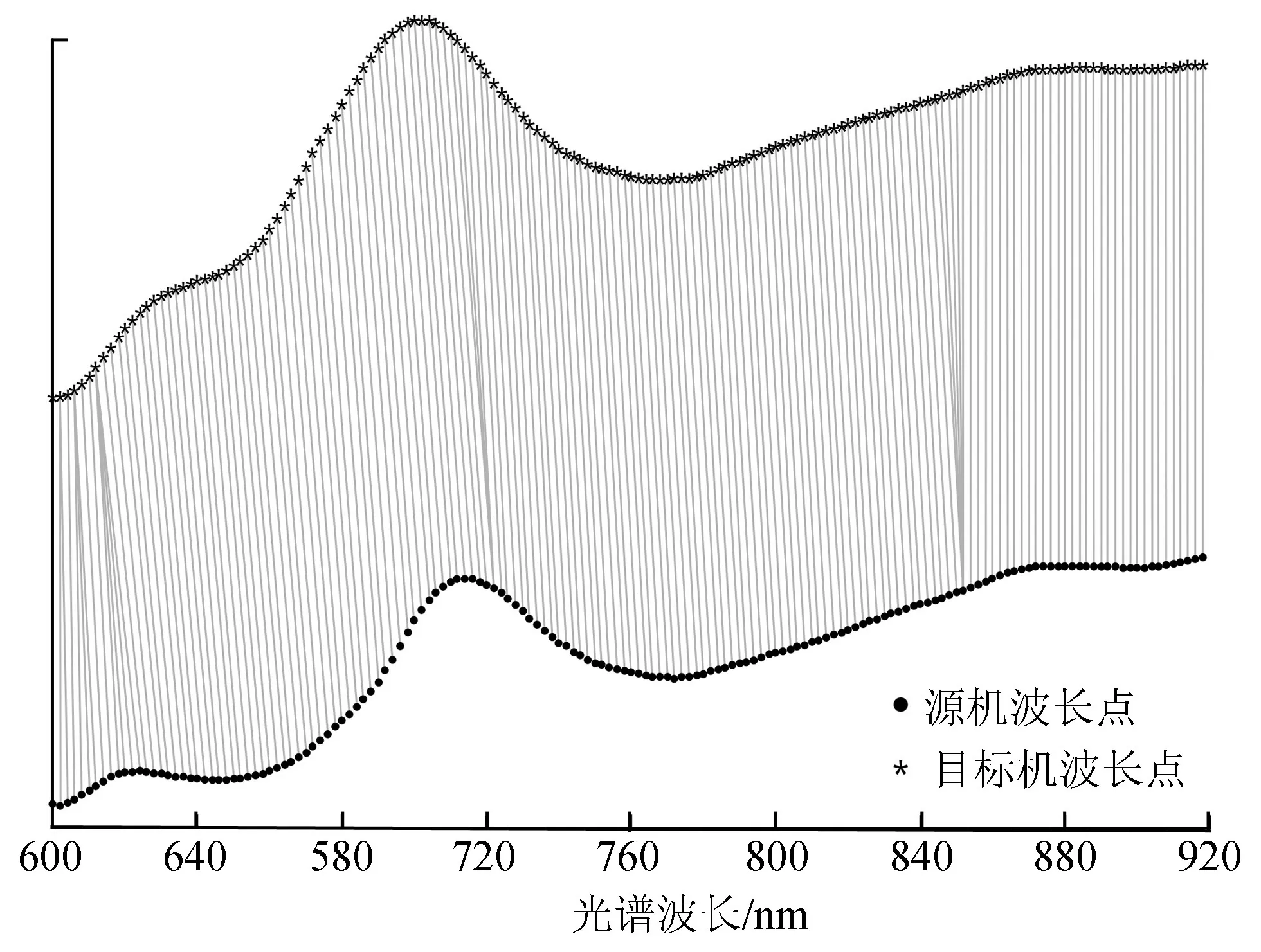
图3 波长点的匹配关系

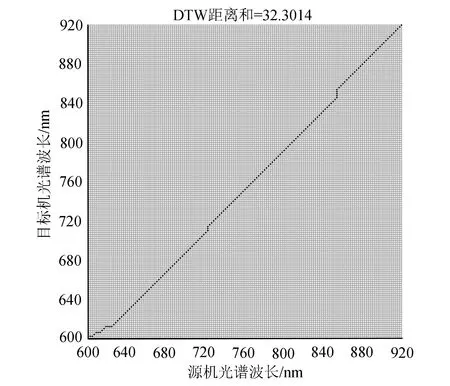
图4 两台近红外光谱仪器的波长的规整路径

玉米数据集里的源机与目标机偏差较小，其光谱波长点单一对应。动态时间规整算法也能找到准确的规整路径，得出准确的关联关系，回归方程部分退化为一元线性回归。

求解上述回归方程，得到转移矩阵F。

3 结果与讨论

3.1 模型传递平均光谱差异对比

使用动态时间规整算法得到转移矩阵F，通过式(14)可计算转移后的目标机光谱。药物数据集上的源机光谱、目标机光谱、传递后的目标机光谱如图5所示。其中目标机光谱和源机光谱差异较大，目标机光谱在传递后和源机光谱的差异则显著减小。

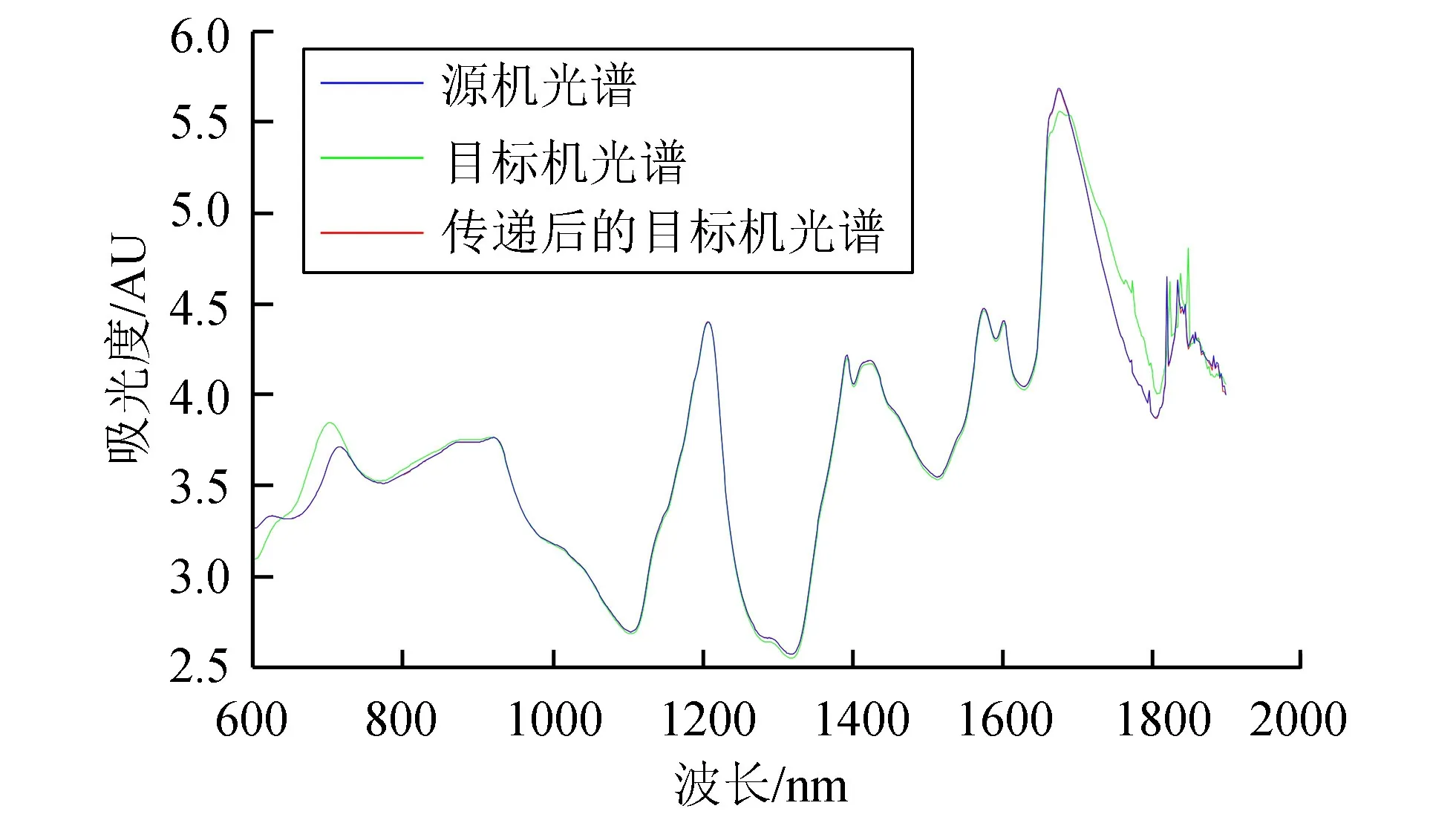
图5 模型传递后的平均光谱

表2为直接校正算法、分段校正算法、动态时间规整算法得到的传递光谱与未传递光谱的平均差异(ARMS)。由表2可看到，光谱的ARMS在应用了模型传递算法后较未传递的光谱均有下降。其中动态时间规整算法传递后的光谱的ARMS整体较小，意味着算法的适用性更好，传递的结果和原机光谱匹配度高、有效。

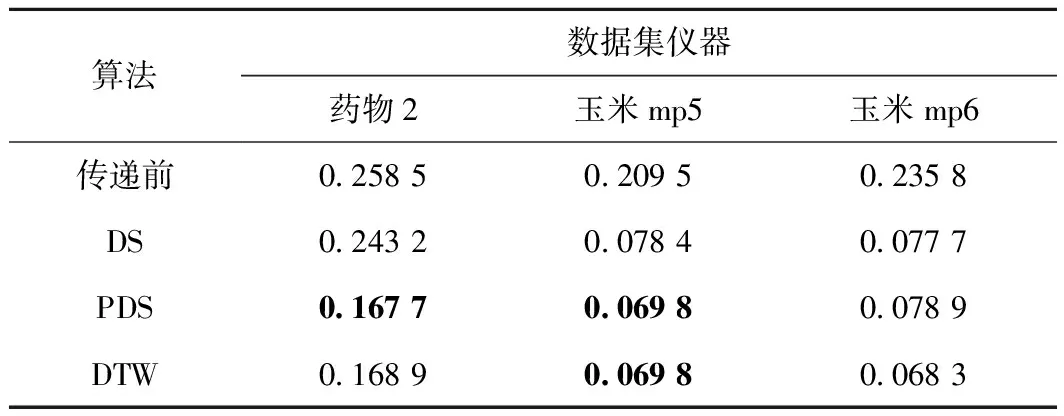
表2 各算法传递光谱的平均差异(ARMS)

3.2 与传统模型传递算法对比

将传递前的光谱和使用直接校正算法、分段校正算法、动态时间规整算法传递后的光谱输入如表1所示的PLS回归模型中预测样本的性质，其预测结果的预测均方偏差(RMSEP)如表3、4所示。其中分段校正算法的窗口大小通过交叉验证确定。

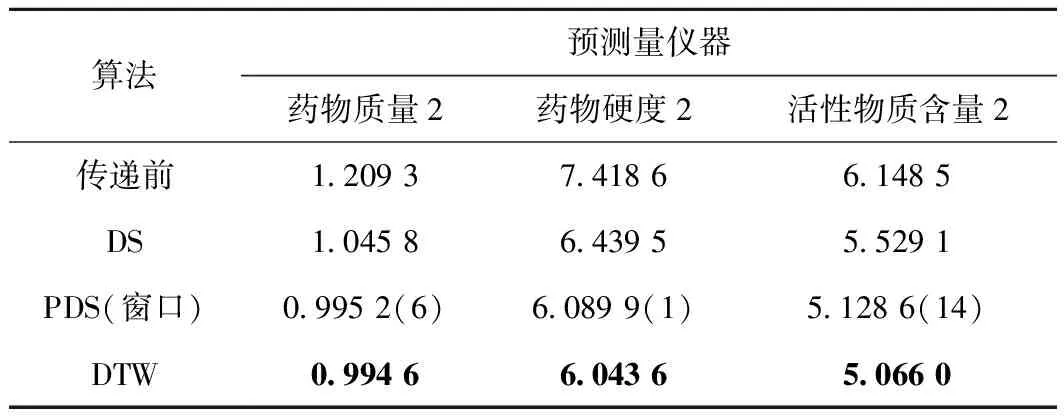
表3 在药物数据集上使用各算法传递光谱的预测均方差(RMESP)

结果表明，直接使用目标机光谱进行预测会由于其和源机光谱的差异产生不客观的预测结果。在使用模型传递算法后，预测结果均有提升。在不同的预测项目中有不同的算法取得优势，使用动态时间规整算法得到的传递后光谱在8项预测中的4项取得领先，故准确度优于直接校正算法和分段校正算法，但由于其运算量大于直接校正算和分段校正法算法，故需要更多的计算时间。

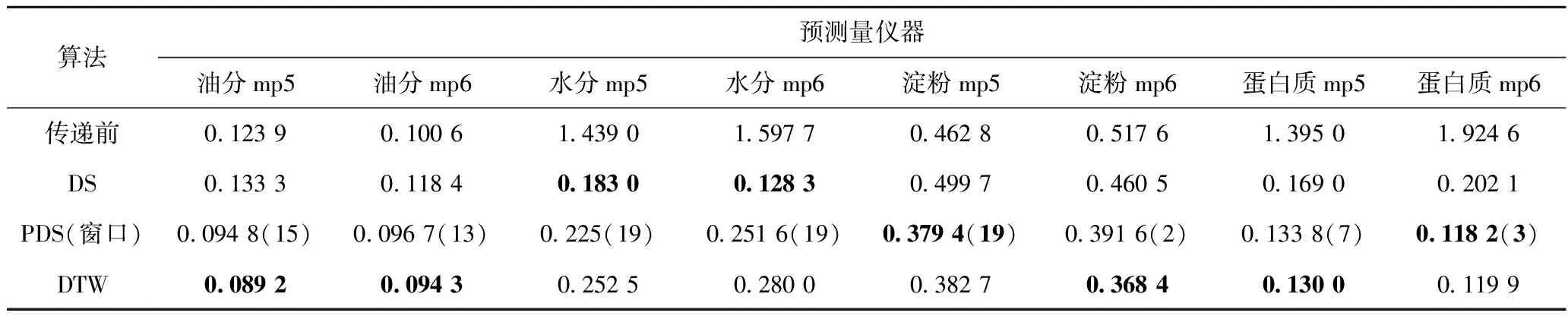
表4 在玉米数据集上使用各算法传递光谱的预测均方差(RMESP)

4 结束语

提出一种新的近红外光谱模型传递算法。该算法依次得到规整路径、匹配关系、回归模型、传递矩阵。使用传递矩阵便可对目标机光谱进行传递，以获得更准确的定量分析的预测结果。在2个数据集上的实验证实了算法的有效性，但计算时间略长。