改进的射电干涉成像凸优化算法
温 珊, 王俊义, 劳保强
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.中国科学院 上海天文台,上海 200030)
射电干涉测量因为高角度分辨率和灵敏度在射电宇宙成像中起着关键作用[1]。然而,由于实际的测量条件的限制,在观测期间获得的能见度测量的数量受到阵列中天线对数量的限制。为了从不完整的数据中重建真实的天空亮度分布,解决这类不适定线性反演问题的图像重建方法一直在发展。为了获得更好的图像质量,作为鲁棒框架的压缩感知(CS)理论被提出来,处理从射电干涉测量中不完全线性测量的稀疏信号恢复。压缩感知引入了一种优于传统奈奎斯特采样范式的信号采集和重构框架,该框架提出了采集信号技术的优化和信号重建的非线性迭代算法[2]。Wiaux等[3]首次提出压缩感知框架应用于射电干涉测量中的图像解卷积,在该框架中,压缩感知方法在图像保真度、灵活性和计算速度上优于传统成像方法。最近,Onose等[4]开发了求解RI成像问题的新算法—交替方向乘子法(ADMM)和原始对偶算法(PD)。它们依赖于近端分裂和前后迭代,在多数据,先验和图像空间中并行运行复杂的类似于CLEAN的迭代。鉴于此,基于交替方向乘子的凸优化算法的数学框架,提出了一种改进的凸优化算法,它保留了与ADMM相同的计算负担,但重构质量在理论上和实验中证明优于前者。仿真和实验结果表明,该方法提高了重建图像的精度和质量。
1 基于压缩感知的射电干涉成像
Donoho等[2]提出了针对稀疏特征信号的压缩感知理论。理论表明,它以低于奈奎斯特采样定理的速率对信号进行采样而不丢失信息,并且可以完整恢复信号。大多数自然信号在某些基也是稀疏或可压缩的,例如天文图像。压缩感知的关键在于由向量x表示的复杂估值信号被认为具有稀疏表示,x=Ψα,其中α∈£D包含只有几个非零元素,在字典Ψ∈£M×N,例如小波基的集合,或更一般地说,一个过度完整的框架[5]。
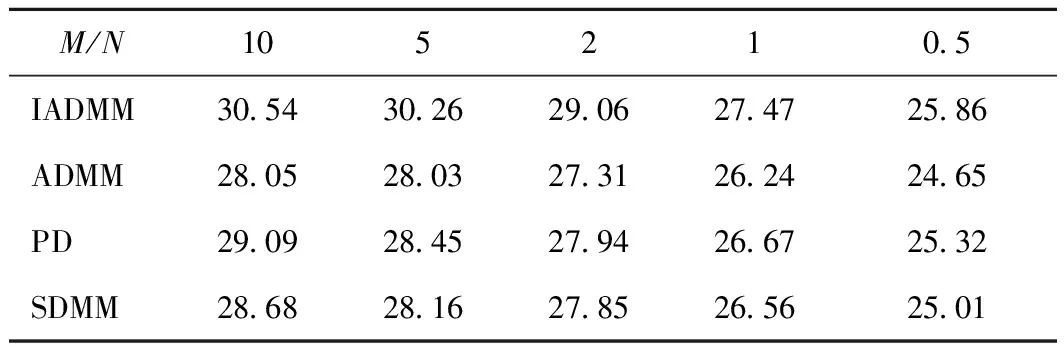
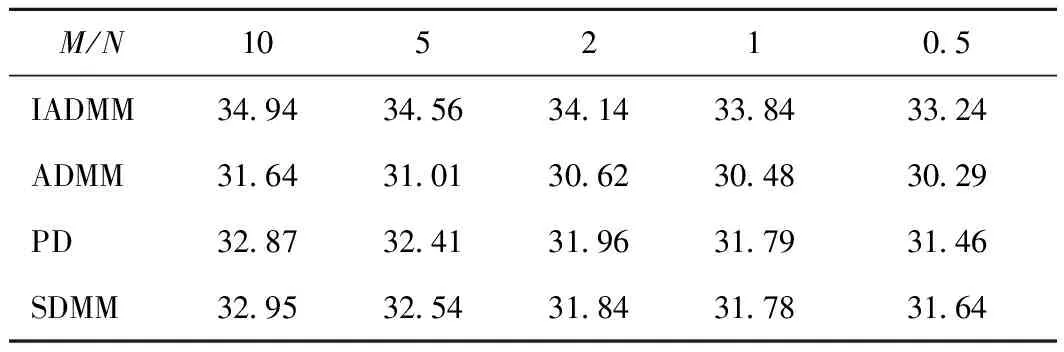
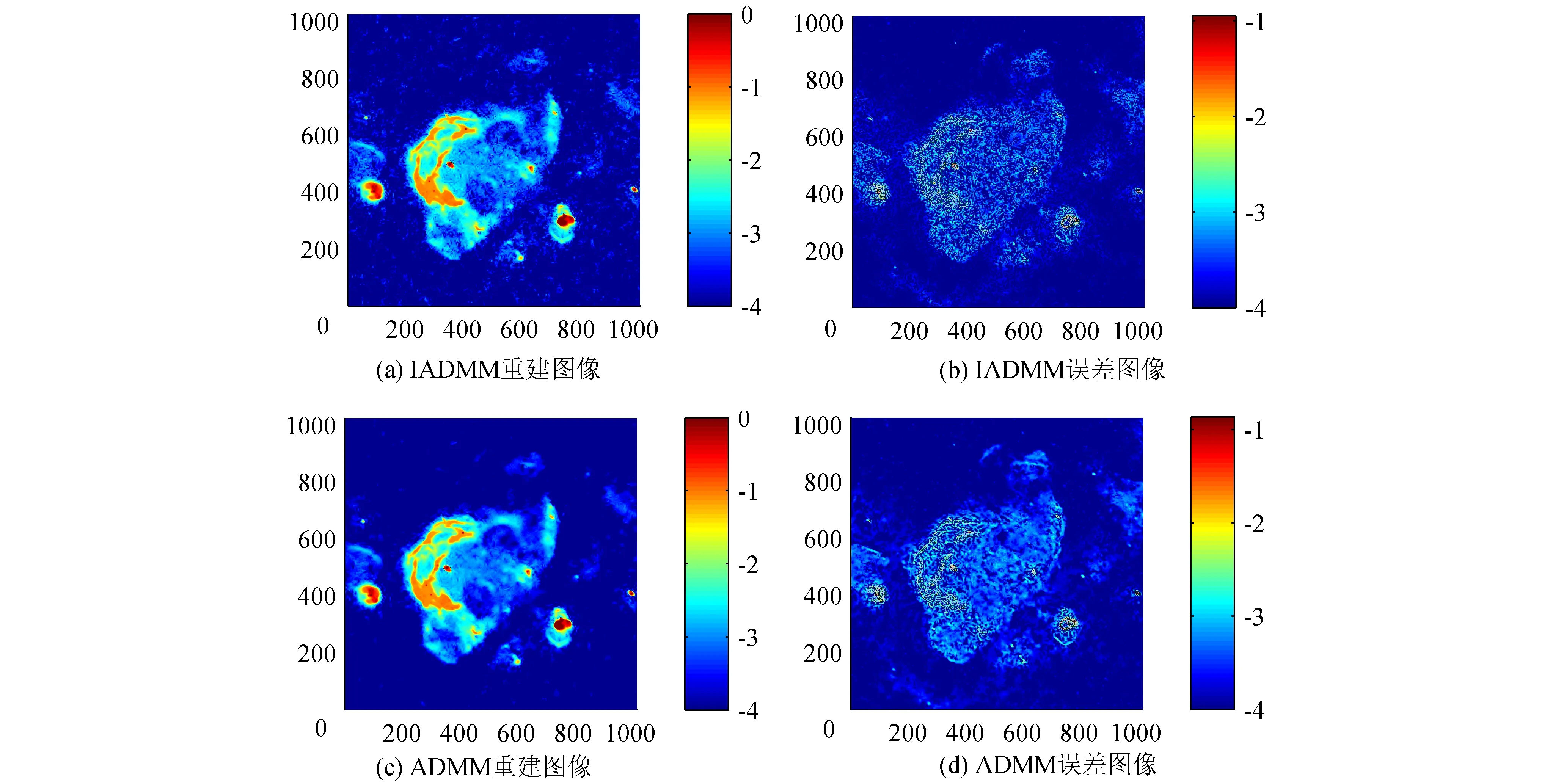
干涉成像被定义为求解测量模型y=Φx+n的不适定逆问题,其中y∈£M表示测量矢量,Φ∈£M×N,其中M (1) 其中:ε为噪声的l2范数的上界;Ψ†为Ψ的伴随算子。由于x是一个强度像,所以也假设了正先验性。数据保真度通过残差低于噪声ε限定。在这里,用最接近的凸松弛l1范数替代稀疏性的模型非凸的l0范数。由于l1最小化问题是一个凸问题,因此可以用有效的凸优化算法来解决。 为了解决式(1)中的不适定逆问题,引入Boyd等[8]提出的用于求解约束优化问题的方法——交替方向乘子法(ADMM)。ADMM是旨在将对偶上升的可分解性与乘子方法的优越收敛性相结合的一种算法。该算法通过式(2)解决问题: minf(x)+g(x) subject toAx+Bz=c, (2) 其中:变量x∈Rn且z∈Rm,A∈Rp×n,B∈Rp×m,c∈Rp。x和z是优化变量。f(x)+g(x)是被由包含变量x的f(x)和涉及变量z的g(x)组成最小化的目标函数。Ax+Bz=c是一个最小化约束。增广的拉格朗日表达式为 Lp(x,z,y)=f(x)+g(z)+yT(Ax+Bz-c)+ (3) (4) uk+1=uk+Axk+1+Bzk+1-c。 (5) 为解决问题(4),简单而有效的方法是引入Gauss-Seidel提出的交替最小化思想,即固定其他变量并交替变量x和z之间的最小化。式(4)可表示为: (6) (7) 式(6)和式(7)阐述了ADMM的基本思想。ADMM的关键思想是在x和z上使用单个Gauss-Seidel,而不是通常的联合最小化。在每次迭代中,x和z以交替方式更新,然后在x更新前z更新后完成双变量u更新。当收敛条件满足时迭代停止,然后x和z获得最优解。ADMM结合了乘子和交替最小化算法的优点成为解决约束优化问题的一个有效的框架,例如图像重建。在接下来的章节中,将回顾基于交替方向乘子的凸优化算法结构[4],以解决射电干涉成像中出现的凸优化任务,并提出一种用于射电干涉成像改进的基于交替方向乘子法的对偶前后向算法。 交替方向乘子法是一种求解优化问题的计算框架,但不具有任何内在的并行结构。为实现并行化处理,Onose等人提出了一种新的凸优化算法—基于交替方向乘子法的对偶前后向算法。式(1)中的重构任务可以使用指示函数作为凸最小化问题来重新定义: =z, (8) 其中,g(z)=iB(z),B={z∈RM:‖Φx-y‖2≤ε}。f(x)=‖Ψ†x‖1+iC(x),iC(x)是凸集C⊂RN的指示函数: (9) 函数iC(x)为复原结果引入了正定性要求。‖Ψ†x‖1表示先验稀疏性,g(z)=iB(z)是数据保真度项,该项约束残差低于由噪声水平ε定义的l2边界。ADMM利用下面的增广拉格朗日函数[8]: (10) 式(10)对函数f和g的平滑性没有明确的假设。在算法上,它们通过在每个原始变量x和z上的最小化之间交替来分割最小化步骤,接着通过梯度上升实现乘子λ的最大化。式(10)中x的最小化不接受闭合形式解[4]。因此,通过执行梯度步骤和邻近步骤来实现前向-后向迭代结构。前向-后向迭代结构通过线性化当前点x(t)处的增广拉格朗日的二次惩罚项并添加近邻项来解决x上的最小化问题。近邻ADMM的迭代更新方程由下式给出: z(t+1)=proxγh(y-Φx(t)-λ(t)), (11) x(t+1)=proxμγf(x(t)-μΦH(λ(t)+Φx(t)- y+z(t+1))), (12) λ(t+1)=λ(t)+β(Φx(t+1)-y+z(t+1)), (13) 其中proxf为函数f的近邻算子[9],定义如下: (14) 其中β和μ为合适的步长。正向梯度步骤通过在与残差的l2范数的梯度相反的方向上执行递减梯度步骤来实现,类似于CLEAN算法的主循环。随后是向后步骤,将近似算子逼近非光滑函数f,类似于CLEAN的次循环[4]。它的解由固定点方程表征: x(t+1)= (15) 在给定的迭代中,它使用FB迭代执行梯度步骤和在给定基Ψ†中执行软阈值操作。前向(梯度)步骤在于与残差的l2范数的梯度相反的方向更新。它类似于CLEAN的一个主要循环。后向(软阈值)步骤包括将阈值以上的所有Ψ†x系数的绝对值减小到阈值以上,并将阈值以下的那些系数设置为零。该步骤与CLEAN的次循环相似,其中软阈值与环路增益因子类似。 3.2.1 基于交替方向乘子法的两步法 为了提高重建高分辨率天文图像的质量,提出一种改进的基于交替方向乘子法的对偶前后向法,它保留了ADMM的计算简便性,但重建质量明显提高。改进算法称之为IADMM。该算法的设计方法是仿照文献[10]的思想,通过对式(15)中解x进行二次加权更新,其定义如下: (16) 在算法1中详细描述了所得到的改进算法。该算法由前向步骤和后向步骤组成。前向步骤对应于梯度步骤,后向步骤通过近邻算子执行隐式子梯度步骤。整个算法流程为: 算法1IADMM 输入:y,F,M,Z,G,Ψ,κ,ρ,d 输出:重建图像x 1:初始值x(0),h(0),g(0),s(0),d0 2:循环t=1,2, 3:p(t)=MFZx(t) 4:h(t)=Gρ(t)+g(t-1) 5:g(t)=g(t-1)+ρ(Gp(t)-h(t)) 6:s(t)=G†(Gp(t)+h(t)-g(t)) 10:直至收敛 11:Γ(Z,κ) 12:循环t=1,2, 13:初始值:q(0),z(0),η 14:Re=ηq(k-1)+Ψ†z(k-1) 16:z(k)=z(k-1)-Ψq(k) 17:直至收敛 18:返回z(k) 3.2.2 复杂度 (17) 实验通过从模拟不完整可见度复原测试图像来评估IADMM的重建性能。在所有测试中,使用的测试图像是M31galaxy的256×256图像,W28 supernova remnant的1024×1024图像和Cygnus A的477×1025图像。亮度值在区间[0.01,1],在图1中以log10标度显示。 图1 测试图像 IADMM与所有其他基准算法进行比较的SNR结果如图2所示,其显示了IADMM、PD、ADMM和SDMM的SNR随M31测试图像的迭代次数而变化的情况。在这个测试中,输入数据被分成4个块,小波级别被设置为4,可见度设置为M=10N。可见度被高斯噪声干扰产生20 dB的ISNR。参数κ为归一化阈值并且控制收敛速度。当κ=10-3到κ=10-5通常产生良好且一致的性能。实验结果表明,对于所有不同的迭代次数,IADMM都优于其他方法。在达到收敛之前,随着迭代次数的增加,SNR增加。如图2所示,改进算法IADMM产生的SNR至少在前期迭代中大约是SDMM的2倍。此外,对于所有次数的迭代,IADMM都比ADMM增益1~2 dB。值得注意的是,迭代次数对IADMM和ADMM的SNR变化率影响较小,这表明它们具有更好的鲁棒性。实验表明,IADMM比现有技术的方法具有更好的重建质量。 图2 以M31为测试图像的4个算法SNR随迭代次数变化的函数 接下来继续从不同的可见度M对IADMM、ADMM、PD和SDMM算法的性能进行研究。M31和Cygnus A的重建结果分别如表1、2所示,它们分别显示了当所使用的可见度M的数量是10N,5N,2N,1N和0.5N所重建得到的SNR。实验中,输入数据被分成16个块,参数κ=10-3。结果表明,IADMM在所有不同的可见度方面均优于其他方法。如表1、2所示,PD和SDMM在M31和Cygnus A中显示出相似的重建结果。值得注意的是,表1中M31的结果显示IADMM的SNR有明显提高,对于较大的可见度覆盖范围,比ADMM提高了2 dB的增益,同时又比PD和SDMM提高1 dB左右。随着可见性数量的增加,改进算法的优点更加明显。对于更复杂的图像Cygnus A,改进算法的优势更明显,在表2中结果显示IADMM的SNR ADMM提高约3 dB。此外,与PD和SDMM相比,改进后的算法在所有可见度下均可实现约2 dB的增益。值得注意的是,增加更多的数据能提高重建的SNR,因为噪声平均得更好。但是,当增加更可见度数据时,SNR增益会稍微停滞,主要是因为频率平面中的某些点仍未覆盖。 表1 以M31为测试图像的4个算法SNR在不同可见度M的结果 最后,从视觉评估上比较IADMM与ADMM的重建性能。在图3中,(a)和(b)显示的分别是IADMM算法下重建图像和误差图像,(c)和(d)显示的分别是ADMM算法下重建图像和误差图像。图3给出对于M=N,κ=10-3和输入信噪比为20 dB的W28的重建结果:IADMM(28.82 dB)和ADMM(26.74 dB)。图3的结果表明,IADMM实现了更好的SNR,与其他方法相比,IADMM仍然提高达到了2 dB左右增益。很显然,2种方法都能为W28带来好复原效果,都能够恢复光源周围的模糊区域。从视觉上看,IADMM产生的重建图像在背景区域中具有较少的伪影,并且在结构化的内部区域中比在其他方法中具有较小的误差。 表2 以Cygnus A为测试图像的4个算法SNR在不同可见度M的结果 图3 W28的重建结果 针对射电干涉成像中产生的凸优化任务,提出了一种改进的射电干涉成像凸优化算法。基于ADMM算法高度可并行化的结构,在ADMM的正向(梯度)步骤中通过对复原结果引入加权二次更新。其设计思想为更新方程取决于前两个结果估计,而不仅仅是前一个。整个算法并行地执行近邻和梯度更新,其可以看作由在多数据、先验和图像空间中并行运行近邻分裂和FB更新组成。通过u-v覆盖模拟和使用不同星系的可见度来研究改进算法。实验结果表明,改进后的算法不仅可保持与ADMM相同的并行实现结构和相同的计算负担,而且可实现更好的噪声图像重构。2 交替方向乘子法
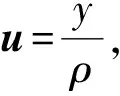
3 改进的凸优化射电干涉成像算法
3.1 基于交替方向乘子法的对偶前后向算法

3.2 改进的基于交替方向乘子法的对偶前后向算法
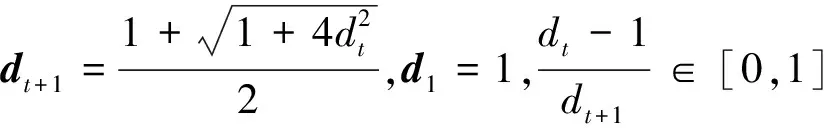
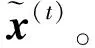
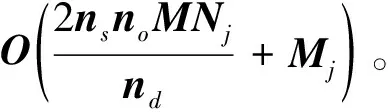
4 仿真结果
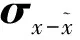
4.1 参数选择
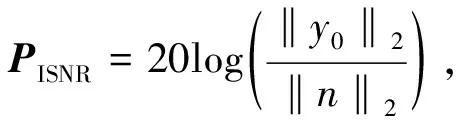
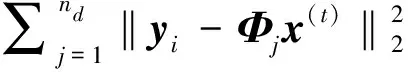
4.2 结果与分析


5 结束语

